Колебания, возникающие под действием внешней периодически изменяющейся силы, называются вынужденными механическими колебаниями. 5 страница
В связи с обнаружением релятивистского эффекта замедления хода часов в свое время возникла проблема «парадокса часов» (иногда рассматривается как «парадокс близнецов»), вызвавшая многочисленные дискуссии. Представим себе, что осуществляется фантастический космический полет к звезде, находящейся на расстоянии 500 световых лет (расстояние, на которое свет от звезды до Земли доходит за 500 лет), со скоростью, близкой к скорости света ( 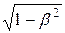 = 0,001). По земным часам полет до звезды и обратно продлится 1000 лет, в то время как для системы корабля и космонавта в нем такое же путешествие займет всего 1 год. Таким образом, космонавт возвратится на Землю в 1/
= 0,001). По земным часам полет до звезды и обратно продлится 1000 лет, в то время как для системы корабля и космонавта в нем такое же путешествие займет всего 1 год. Таким образом, космонавт возвратится на Землю в 1/ 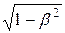 раз более молодым, чем его брат-близнец, оставшийся на Земле. Это явление, получившее название парадокса близнецов,в действительности парадокса не содержит. Дело в том, что принцип относительности утверждает равноправность не всяких систем отсчета, а только инерциальных. Неправильность рассуждения состоит в том, что системы отсчета, связанные с близнецами,– не эквивалентны: земная система инерциальна, а корабельная – неинерциальна, поэтому к ним принцип относительности неприменим.
раз более молодым, чем его брат-близнец, оставшийся на Земле. Это явление, получившее название парадокса близнецов,в действительности парадокса не содержит. Дело в том, что принцип относительности утверждает равноправность не всяких систем отсчета, а только инерциальных. Неправильность рассуждения состоит в том, что системы отсчета, связанные с близнецами,– не эквивалентны: земная система инерциальна, а корабельная – неинерциальна, поэтому к ним принцип относительности неприменим.
Релятивистский эффект замедления хода часов является совершенно реальным и получил экспериментальное подтверждение при изучении нестабильных, самопроизвольно распадающихся элементарных частиц в опытах с 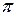 -мезонами. Среднее время жизни покоящихся
-мезонами. Среднее время жизни покоящихся 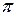 -мезонов (по часам, движущимся вместе с ними)
-мезонов (по часам, движущимся вместе с ними) 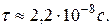 Следовательно,
Следовательно, 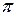 -мезоны, образующиеся в верхних слоях атмосферы (на высоте «30 км) и движущиеся со скоростью, близкой к скорости света, должны были бы проходить расстояния
-мезоны, образующиеся в верхних слоях атмосферы (на высоте «30 км) и движущиеся со скоростью, близкой к скорости света, должны были бы проходить расстояния 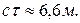 , т.е. не могли бы достигать земной поверхности, что противоречит действительности. Объясняется это релятивистским эффектом замедления хода времени: для земного наблюдателя срок жизни
, т.е. не могли бы достигать земной поверхности, что противоречит действительности. Объясняется это релятивистским эффектом замедления хода времени: для земного наблюдателя срок жизни 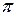 -мезона
-мезона 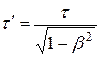 , а путь этих частиц в атмосфере
, а путь этих частиц в атмосфере 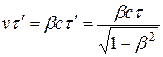 . Так как
. Так как 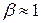 , то
, то 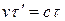 .
.
3. Длина тел в разных системах отсчета.Рассмотрим стержень, расположенный вдоль оси х' и покоящийся относительно системы К'. Длина стержня в системе К' будет 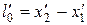 , где
, где 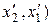 – не изменяющиеся со временем
– не изменяющиеся со временем 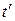 координаты конца и начала стержня, а индекс 0 показывает, что в системе отсчета К' стержень покоится. Определим длину этого стержня в системе К, относительно которой он движется со скоростью v. Для этого необходимо измерить координаты его концов
координаты конца и начала стержня, а индекс 0 показывает, что в системе отсчета К' стержень покоится. Определим длину этого стержня в системе К, относительно которой он движется со скоростью v. Для этого необходимо измерить координаты его концов 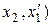 в системе К в один и тот же момент времени t. Их разность
в системе К в один и тот же момент времени t. Их разность 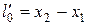 и даст длину стержня в системе К. Используя преобразования Лоренца (13.8), получим
и даст длину стержня в системе К. Используя преобразования Лоренца (13.8), получим
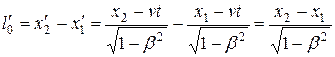 ,
,
т.е. 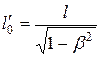 (13.12)
(13.12)
Таким образом, длина стержня, измеренная в системе, относительно которой он движется, оказывается меньше длины, измеренной в системе, относительно которой стержень покоится. Если стержень покоится в системе К, то, определяя его длину в системе К', опять-таки придем к выражению (13.12).
Из выражения (13.12) следует, что линейный размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении движения 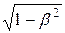 раз, т.е. так называемое лоренцево сокращение длинытем больше, чем больше скорость движения. Из второго и третьего уравнений преобразований Лоренца (13.8) следует, что
раз, т.е. так называемое лоренцево сокращение длинытем больше, чем больше скорость движения. Из второго и третьего уравнений преобразований Лоренца (13.8) следует, что 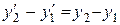 ,
, 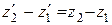 , т.е. поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета. Таким образом, линейные размеры тела наибольшие в той инерциальной системе отсчета, относительно которой тело покоится.
, т.е. поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета. Таким образом, линейные размеры тела наибольшие в той инерциальной системе отсчета, относительно которой тело покоится.
4. Преобразование и сложение скоростей.Рассмотрим движение материальной точки в системе К', в свою очередь движущейся относительно системы К со скоростью v. Определим скорость этой же точки в системе К. Если в системе К движение точки в каждый момент времени t определяется координатами х, у, z, а в системе К' в момент времени 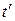 – координатами х', у', z', то
– координатами х', у', z', то 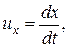
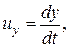
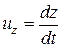 и
и 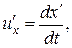
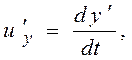
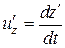 представляют собой соответственно проекции на оси х, у, z и х', у', z' вектора скорости рассматриваемой точки относительно систем К и
представляют собой соответственно проекции на оси х, у, z и х', у', z' вектора скорости рассматриваемой точки относительно систем К и 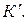
Согласно преобразованиям Лоренца (13.8),
.
Произведя соответствующие преобразования, получаем релятивистский закон сложения скоростей специальной теории относительности:
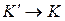
| 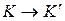
|
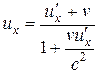 , ,
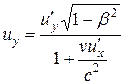 , ,
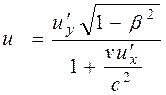
| 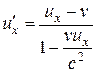 , ,
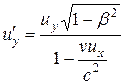 , (13.13) , (13.13)
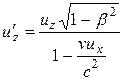 . .
|
Если материальная точка движется параллельно оси х, то скорость и относительно системы К совпадает с их, а скорость и' относительно К' – с и'х. Тогда закон сложения скоростей примет вид
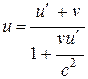 ,
, 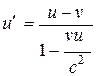 (13.14)
(13.14)
Легко убедиться в том, что если скорости v, и' и и малы по сравнению со скоростью света с, то формулы (13.14) и (13.13) переходят в закон сложения скоростей в классической механике. Таким образом, законы релятивистской механики в предельном случае для малых скоростей (по сравнению со скоростью света) переходят в законы классической физики, которая, следовательно, является частным случаем механики Эйнштейна для малых скоростей.
Релятивистский закон сложения скоростей подчиняется второму постулату Эйнштейна. Действительно, если 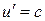 , то формула (13.14)) примет вид
, то формула (13.14)) примет вид 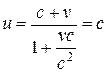 (аналогично можно показать, что при
(аналогично можно показать, что при 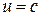 скорость и' также равна с). Этот результат свидетельствует о том, что релятивистский закон сложения скоростей находится в согласии спостулатами Эйнштейна.
скорость и' также равна с). Этот результат свидетельствует о том, что релятивистский закон сложения скоростей находится в согласии спостулатами Эйнштейна.
Докажем также, что если складываемые скорости сколь угодно близки к скорости света с, то их результирующая скорость будет всегда меньше или равна с. Вкачестве примера рассмотрим предельный случай u' = v = c. После подстановки в формулу (13.14) получим и = с. Таким образом, при сложении любых скоростей результат не может превысить скорости света с в вакууме. Скорость света в вакууме есть предельная скорость, которую невозможно превысить.
5. Интервал между событиями
Преобразования Лоренца и следствия из них приводят к выводу об относительности длин и промежутков времени, значение которых в различных системах отсчета разное. В то же время относительный характер длин и промежутков времени в теории Эйнштейна означает относительность отдельных компонентов какой-тореальной физической величины, не зависящей от системы отсчета, т.е. являющейся инвариантной по отношению к преобразованиям координат. В четырехмерном пространстве Эйнштейна, в котором каждое событие характеризуется четырьмя координатами 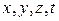 , такой физической величиной является интервал между двумя событиями:
, такой физической величиной является интервал между двумя событиями:
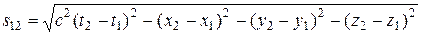 , (13.15)
, (13.15)
где 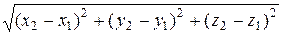 – расстояние между точками обычного трехмерного пространства, в которых эти события произошли. Введя обозначение
– расстояние между точками обычного трехмерного пространства, в которых эти события произошли. Введя обозначение 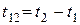 ,
, 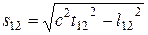 , покажем, что интервал между двумя событиями одинаков во всех инерциальных системах отсчета. Обозначив
, покажем, что интервал между двумя событиями одинаков во всех инерциальных системах отсчета. Обозначив 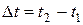 ,
, 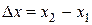 ,
, 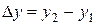 ,
, 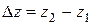 , выражение (13.15) можно записать в виде
, выражение (13.15) можно записать в виде 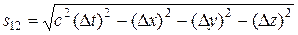 .
.
Интервал между теми же событиями в системе К' равен
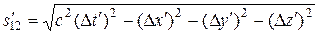 (13.16)
(13.16)
Согласно преобразованиям Лоренца (13.8),
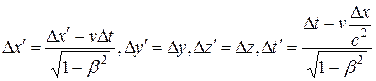 .
.
Подставив эти значения в (13.16), после элементарных преобразований получим, что 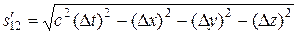 , т.е.
, т.е. 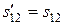 .
.
Обобщая полученные результаты, можно сделать вывод, что интервал, определяя пространственно-временные соотношения между событиями, является инвариантом при переходе от одной инерциальной системы отсчета к другой. Инвариантность интервала означает, что, несмотря на относительность длин и промежутков времени, течение событий носит объективный характер и не зависит от системы отсчета.
Теория относительности, таким образом, сформулировала новое представление о пространстве и времени, обобщенное далее в диалектическом материализме. Пространственно-временные отношения являются не абсолютными величинами, как утверждала механика Галилея-Ньютона, а относительными. Следовательно, представления об абсолютном пространстве и времени являются несостоятельными. Кроме того, инвариантность интервала между двумя событиями свидетельствует о том, что пространство и время органически связаны между собой и образуют единую форму существования материи – пространство-время. Пространство и время не существуют вне материи и независимо от нее.
Дальнейшее развитие теории относительности (общая теория относительности,или теория тяготения)показало, что свойства пространства-времени в данной области определяются действующими в ней полями тяготения. При переходе к космическим масштабам геометрия пространства-времени не является евклидовой (т.е. не зависящей от размеров области пространства-времени), а изменяется от одной области к другой в зависимости от концентрации масс в этих областях и их движения.
6. Основной закон релятивистской динамики материальной точки
Согласно представлениям классической механики, масса тела есть величина постоянная. Однако в конце XIX столетия на опытах с быстро движущимися электронами было установлено, что масса тела зависит от скорости его движения, а именно возрастает с увеличением скорости по закону
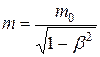 , (13.17)
, (13.17)
где 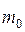 – масса покояматериальной точки, т.е. масса, измеренная в той инерциальной системе отсчета, относительно которой материальная точка находится в покое; с – скорость света в вакууме; т – масса точки в системе отсчета, относительно которой она движется со скоростью и. Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца. Основной закон динамики Ньютона
– масса покояматериальной точки, т.е. масса, измеренная в той инерциальной системе отсчета, относительно которой материальная точка находится в покое; с – скорость света в вакууме; т – масса точки в системе отсчета, относительно которой она движется со скоростью и. Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца. Основной закон динамики Ньютона 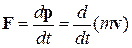 оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса.
оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса.
Основной закон релятивистской динамикиматериальной точки имеет вид
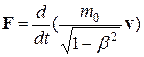 (13.18)
(13.18)
или
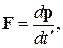 (13.19)
(13.19)
где 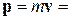
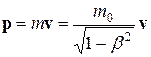 ) (13.20)
) (13.20)
– релятивистский импульсматериальной точки.
Отметим, что уравнение (13.20) внешне совпадает с основным уравнением ньютоновской механики. Однако физический смысл его другой: справа стоит производная по времени от релятивистского импульса, определяемого формулой (13.20). Таким образом, уравнение (13.20) инвариантно по отношению к преобразованиям Лоренца и, следовательно, удовлетворяет принципу относительности Эйнштейна. Следует учитывать, что ни импульс, ни сила не являются инвариантными величинами. Более того, в общем случае ускорение не совпадает по направлению с силой.
В силу однородности пространства в релятивистской механике выполняется закон сохранения релятивистского импульса:релятивистский импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени. Часто вообще не оговаривают, что рассматривают релятивистский импульс, так как если тела движутся со скоростями, близкими к с, то можно использовать только релятивистское выражение для импульса.
Анализ формул (13.17) – (13.19) показывает, что при скоростях, значительно меньших скорости света, уравнение (13.20) переходит в основной закон классической механики. Следовательно, условием применимости законов классической (ньютоновской) механики является условие v<<c. Законы классической механики получаются как следствие теории относительности для предельного случая v<<c (формально переход осуществляется при 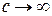 ). Таким образом, классическая механика – это механика макротел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме).
). Таким образом, классическая механика – это механика макротел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме).
Экспериментальное доказательство зависимости массы от скорости (13.20) является подтверждением справедливости специальной теории относительности.
7. Взаимосвязь массы и энергии
Найдем кинетическую энергию релятивистской частицы (материальной точки). Раньше было показано, что приращение кинетической энергии материальной точки на элементарном перемещении равно работе силы на этом перемещении:
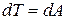 или dT=Fdr(13.21)
или dT=Fdr(13.21)
Учитывая, что dr = v dt, и подставив в (13.21) выражение (13.20), получим 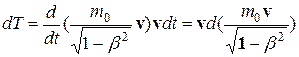 .
.
Преобразовав данное выражение с учетом того, что vdv =vdv, а также учитывая формулу (13.20), придем к выражению
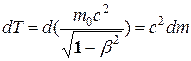 (13.22)
(13.22)
т.е. приращение кинетической энергии частицы пропорционально приращению ее массы.
Так как кинетическая энергия покоящейся частицы равна нулю, а ее масса равна массе покоя т0, то, проинтегрировав (13.22), получим
Т = (т – т0)с (13.23)
или кинетическая энергия релятивистской частицы имеет вид
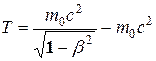 (13.24)
(13.24)
Разлагая в ряд 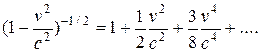 , пренебрегая членами второго порядка малости при v<<c, выражение (13.24) переходит в классическое:
, пренебрегая членами второго порядка малости при v<<c, выражение (13.24) переходит в классическое: 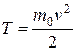 .
.
А.Эйнштейн обобщил положение (13.22), предположив, что оно справедливо не только для кинетической энергии материальной точки, но и для полной энергии, а именно: любое изменение массы 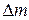 сопровождается изменением полной энергии материальной точки
сопровождается изменением полной энергии материальной точки
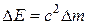 (13.25)
(13.25)
Отсюда А. Эйнштейн пришел к универсальной зависимости между полной энергией тела Е и его массой т:
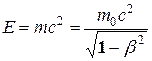 (13.26)
(13.26)
Уравнение (13.26), равно как и (13.25), выражает фундаментальный закон природы – закон взаимосвязи (пропорциональности) массы и энергии:полная энергия системы равна произведению ее массы на квадрат скорости света в вакууме. Отметим, что в полную энергию Е не входит потенциальная энергия тела во внешнем силовом поле.
Учитывая выражение (13.23), закон (13.26) можно записать в виде Е = т0 с2 + Т, откуда следует, что покоящееся тело (Т = 0) также обладает энергией Е0 = т0с2, называемой энергией покоя.Классическая механика энергию покоя Е0 не учитывает, считая, что при v =0 энергия покоящегося тела равна нулю.
В силу однородности времени в релятивистской механике, как и в классической, выполняется закон сохранения энергии:полная энергия замкнутой системы сохраняется, т.е. не изменяется с течением времени.
Из формул (13.26) и (13.20) найдем релятивистское соотношение между полной энергией и импульсом частицы:
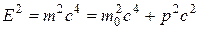 ,
, 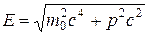 (13.27)
(13.27)
Возвращаясь к уравнению (13.26), отметим еще раз, что оно имеет универсальный характер. Оно применимо ко всем формам энергии, т.е. можно утверждать, что с энергией, какой бы формы она ни была, связана масса
т = Е/с2, (13.28)
и, наоборот, со всякой массой связана определенная энергия (13.20).
Рассматривая выводы специальной теории относительности, видим, что она, как, впрочем, и любые крупные открытия, потребовала пересмотра многих установившихся и ставших привычными представлений. Масса тела не остается постоянной величиной, а зависит от скорости тела; длина тел и длительность событий не являются абсолютными величинами, а носят относительный характер; наконец, масса и энергия оказались связанными друг с другом, хотя они и являются качественно различными свойствами материи.
Эту ломку укоренившихся представлений некоторые философы пытались использовать для распространения двух разновидностей идеализма: энергетизма и философского релятивизма. Первая из этих теорий рассматривала возможность преобразования массы в энергию и, наоборот, энергии в массу, доказывая «эквивалентность материи и энергии». Закон взаимосвязи массы и энергии действительно утверждает, что любые превращения энергии тела сопровождаются изменениями его массы, однако при этом масса не «переходит в энергию». Закон взаимосвязи массы и энергии является подтверждением неразрывности материи и движения – одного из основных положений диалектического материализма.
Основной вывод теории относительности сводится к тому, что пространство и время органически взаимосвязаны и образуют единую форму существования материи – пространство-время. Только поэтому пространственно-временной интервал между двумя событиями является абсолютным, в то время как пространственные и временные промежутки между этими событиями относительны. Следовательно, вытекающие из преобразований Лоренца следствия являются выражением объективно существующих пространственно-временных соотношений движущейся материи.
Контрольные вопросы
1. В чем физическая сущность механического принципа относительности?
2. В чем заключается правило сложения скоростей в классической механике?
3. 3.Каковы причины возникновения специальной теории относительности?
4. В чем заключаются основные постулаты специальной теории относительности?
5. Зависит ли от скорости движения системы отсчета скорость тела? скорость света?
6. Запишите и прокомментируйте преобразования Лоренца. При каких условиях они переходят в преобразования Галилея?
7. Какой вывод о пространстве и времени можно сделать на основе преобразований Лоренца?
8. 8.Одновременны ли события в системе К', если в системе К они происходят в одной точке и одновременны? в системе А" события разобщены, но одновременны? Обосновать ответ.
9. Какие следствия вытекают из специальной теории относительности для размеров тел и длительности событий в разных системах отсчета? Обосновать ответ.
10. При какой скорости движения релятивистское сокращение длины движущегося тела составит 25%?
11. В чем состоит «парадокс близнецов» и как его разрешить?
12. В чем заключается релятивистский закон сложения скоростей? Как показать, что он находится в согласии с постулатами Эйнштейна?
13. Как определяется интервал между событиями? Доказать, что он является инвариантом при переходе от одной инерциальной системы отсчета к другой.
14. Какой вид имеет основной закон релятивистской динамики материальной точки? Чем он отличается от основного закона ньютоновской механики?
15. В чем заключается закон сохранения релятивистского импульса? релятивистской массы?
16. Как выражается кинетическая энергия в релятивистской механике?
17. При каком условии релятивистская формула для кинетической энергии переходит в классическую формулу?
18. Сформулируйте и запишите закон взаимосвязи массы и энергии. В чем его физическая сущность? Приведите примеры его экспериментального подтверждения.
Учебное издание
Дата добавления: 2015-08-08; просмотров: 808;
