Потенциальная энергия упруго деформированного стержня равна 3 страница
3. Силы инерции при ускоренном поступательном движении
системы отсчета
Пусть на потолке вагона на нити висит шарик массой m. Пока вагон покоится и движется равномерно и прямолинейно, нить, удерживающая шарик, занимает вертикальное положение. При этом сила тяжести 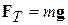 уравновешивается реакцией нити
уравновешивается реакцией нити 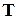 .
.
Если вагон поезда набирает скорость, то нить отклонится от вертикали назад (рис. 10.3).
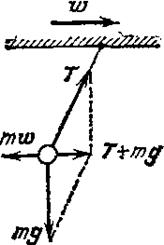
| Рис.10.3 |
Обозначим ускорение поезда 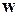 . Относительно Земли (которую мы считаем инерциальной системой отсчета) шарик имеет такое же ускорение
. Относительно Земли (которую мы считаем инерциальной системой отсчета) шарик имеет такое же ускорение 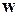 ,как и вагон. Это ускорение сообщается шарику силой
,как и вагон. Это ускорение сообщается шарику силой 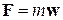 . Она равна сумме силы натяжения нити Т и силы тяжести
. Она равна сумме силы натяжения нити Т и силы тяжести 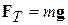 , т.е.
, т.е. 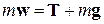 . Относительно системы отсчета, связанной с ускоренно движущимся вагоном, шарик покоится. Отсутствие ускорения шарика относительно вагона можно объяснить тем, что сила
. Относительно системы отсчета, связанной с ускоренно движущимся вагоном, шарик покоится. Отсутствие ускорения шарика относительно вагона можно объяснить тем, что сила 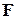 уравновешивается силой инерции, равной (
уравновешивается силой инерции, равной ( 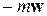 ), так как на шарик никакие друге силы не действуют.
), так как на шарик никакие друге силы не действуют.
Проявление сил инерции при поступательном движении наблюдается в повседневных явлениях. Например, когда поезд набирает скорость, пассажир, сидящий по ходу поезда, под действием силы инерции прижимается к спинке сиденья. Наоборот, при торможении поезда сила инерции направлена в противоположную сторону, и пассажир отделяется от спинки сиденья. Силы инерции особенно заметны при внезапных торможениях поезда. Они проявляются в перегрузках, которые возникают при запуске и торможении космических кораблей.
4. Силы инерции при равномерном вращательном
движении системы отсчета. Центробежная сила инерции
Рассмотрим поведение тел в системе отсчета К', вращающейся относительно инерциальной системы К с постоянной угловой скоростью 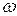 : в системе отчета К' поступательная составляющая движения отсутствует. Ясно, что она неинерциальна. Примером рассматриваемого движения может служить система, связанная с вращающимся диском электропроигрывателя.
: в системе отчета К' поступательная составляющая движения отсутствует. Ясно, что она неинерциальна. Примером рассматриваемого движения может служить система, связанная с вращающимся диском электропроигрывателя.
Укрепим на диске радиально направленный стержень, на который наденем шарик, «привязанный» к оси диска пружиной (рис. 10.4).
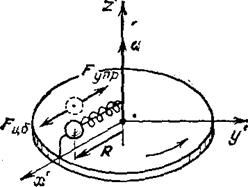
| Рис. 10.4. Шарик может перемещаться только вдоль радиуса диска, скользя без трения по тонкому стержню |
Пока диск не вращается, пружина не деформирована. При раскручивании диска шарик растягивает пружину до тех пор, пока упругая сила 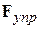 не станет равной произведению массы шарика на его ускорение. Обозначим через
не станет равной произведению массы шарика на его ускорение. Обозначим через 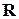 – радиус – вектор, проведенный к шарику от центра диска и перпендикулярно к оси вращения. Его модуль дает расстояние R шарика от оси вращения системы К'. Так как шарик движется от центра и вдоль радиуса окружности вместе с равномерно вращающимся диском, ускорение шарика равно по модулю центростремительному ускорению и направлено противоположно ему:
– радиус – вектор, проведенный к шарику от центра диска и перпендикулярно к оси вращения. Его модуль дает расстояние R шарика от оси вращения системы К'. Так как шарик движется от центра и вдоль радиуса окружности вместе с равномерно вращающимся диском, ускорение шарика равно по модулю центростремительному ускорению и направлено противоположно ему:
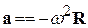 (10.4)
(10.4)
Таким образом, при вращении диска
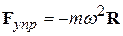 (10.5)
(10.5)
Относительно системы отсчета К', связанной с диском, шарик покоится. Формально это можно объяснить тем, что в данной системе кроме силы 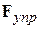 на шарик действует сила инерции
на шарик действует сила инерции
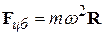 , (10.6)
, (10.6)
направленная вдоль радиуса от оси вращения диска.
Определяемая выражением (10.6) сила 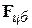 называется центробежной силой инерции. Она возникает во вращающихся системах отсчета и не зависит от того, покоится тело в этой системе или движется относительно нее со скоростью. Это следует из того, что скорость не входит в формулу (10.6).
называется центробежной силой инерции. Она возникает во вращающихся системах отсчета и не зависит от того, покоится тело в этой системе или движется относительно нее со скоростью. Это следует из того, что скорость не входит в формулу (10.6).
Земля подобна гигантскому вращающемуся шару. Поэтому, рассматривая поведение тел в системе отсчета, связанного с Землей, при точных расчетах нужно учитывать центробежную силу инерции. Эта сила максимальна на экваторе. За сутки, т.е. за 86400 с, Земля поворачивается на угол 2 л. Следовательно, угловая скорость Земли 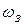 = 2л : 86400 = 7,27 • 10-5рад/с.
= 2л : 86400 = 7,27 • 10-5рад/с.
Согласно формуле (10.6) модуль центробежной силы инерции, действующей на экваторе на тело массой 1 кг, равен Fцб = 1,00·(7,27·10-5)2·6,38·10б = 0,0337 Н, что составляет 1/291 часть силы тяжести mg, равной 9,81 Н. Отсюда следует, что при рассмотрении движения тел относительно Земли в ряде случаев центробежной силой инерции можно пренебречь.
Влияние центробежной силы наиболее существенно на вес тела. С целью изучения проявления данного эффекта рассмотрим тело массой m, находящееся вблизи поверхности Земли на широте 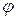 (рис.10.5). Ускорение свободного падения g есть ускорение тела относительно Земли, т.е. ускорение во вращающейся системе отсчета. В этой системе кроме гравитационной силы Fg, с которой Земля притягивает тело, нужно учитывать и центробежную силу инерции.
(рис.10.5). Ускорение свободного падения g есть ускорение тела относительно Земли, т.е. ускорение во вращающейся системе отсчета. В этой системе кроме гравитационной силы Fg, с которой Земля притягивает тело, нужно учитывать и центробежную силу инерции.
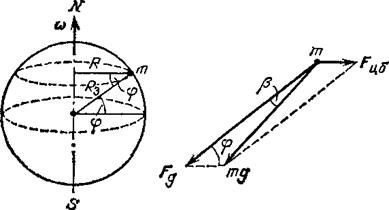
| Рис.10.5. |
Сила тяжести тg является результирующей сил Fg и 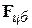 , т.е.
, т.е. 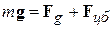 .
.
Как видно из рисунка, тело отстоит от оси вращения на расстоянии 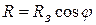 . Тогда величина центробежной силы равно
. Тогда величина центробежной силы равно 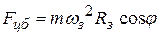 .
.
Направление силы mg совпадает с направлением нити, натянутой грузом, которое называется направлением отвеса или вертикальным направлением. Из рис. 10.5 видно, что направление отвеса не совпадает с направлением к центру Земли, образуя с ним угол 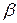 . Для определения этого угла воспользуемся теоремой синусов, согласно которой отношение сторон треугольника равно отношению синусов противолежащих этим сторонам углов. Углу
. Для определения этого угла воспользуемся теоремой синусов, согласно которой отношение сторон треугольника равно отношению синусов противолежащих этим сторонам углов. Углу 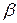 противолежит сторона треугольника, длина которой численно равна
противолежит сторона треугольника, длина которой численно равна 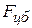 , углу
, углу 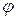 – сторона, длина которой численно равно тg. Следовательно,
– сторона, длина которой численно равно тg. Следовательно, 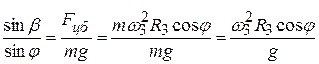 .
.
Отсюда следует, что 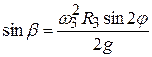 . Подставляя известные значения
. Подставляя известные значения 
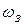 = 2л : 86400 = 7,27 • 10-5рад/с,
= 2л : 86400 = 7,27 • 10-5рад/с, 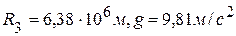 ,
,  получим
получим 
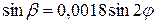 (10.7)
(10.7)
Из (10.7) следует, что отклонение отвеса равно нулю на экваторе, где 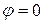 , и на полюсах, где
, и на полюсах, где 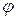 =90°, а на широте
=90°, а на широте 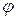 = 45° равно 0,0018 рад или 6'. Разность Fg – mg равна нулю на полюсах и достигает максимума, равного 0,3% силы тg, на экваторе. Из-за сплюснутости Земли сила Ре сама по себе изменяется с широтой, будучи на полюсах на 0,2 % больше, чем на экваторе. В итоге ускорение свободного падения изменяется с широтой от 9,780 м/с2 на экваторе до 9,832 м/с2 на полюсах. Значение g = 9,80665 м/с2 принято в качестве нормального (стандартного) значения.
= 45° равно 0,0018 рад или 6'. Разность Fg – mg равна нулю на полюсах и достигает максимума, равного 0,3% силы тg, на экваторе. Из-за сплюснутости Земли сила Ре сама по себе изменяется с широтой, будучи на полюсах на 0,2 % больше, чем на экваторе. В итоге ускорение свободного падения изменяется с широтой от 9,780 м/с2 на экваторе до 9,832 м/с2 на полюсах. Значение g = 9,80665 м/с2 принято в качестве нормального (стандартного) значения.
5. Сила Кориолиса
Рассмотрим тела, неподвижные относительно вращающейся системы отсчета. При движении тела кроме центробежной возникает еще одна сила инерции, называемая силой Кориолиса или кориолисовой силой.
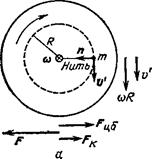
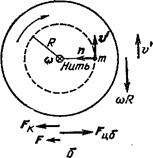
Возьмем горизонтально расположенный диск, вращающийся относительно инерциальной системы отсчета (которую мы для краткости будем называть неподвижной) с постоянной угловой скоростью 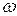 (рис.10.6). Допустим, что по окружности радиуса R равномерно движется привязанная нитью к оси диска материальная точка (частица) со скоростью v' относительно диска.
(рис.10.6). Допустим, что по окружности радиуса R равномерно движется привязанная нитью к оси диска материальная точка (частица) со скоростью v' относительно диска.
| 
|
| Рис.10.6. Справа от дисков показаны направления скоростей, под диском – направления сил: а – совпадают, б – противоположны. |
Линейная скорость точек окружности равна 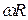 . В случае, изображенном на рис. 10.6 а, скорость v частицы относительно неподвижной системы имеет модуль, равный
. В случае, изображенном на рис. 10.6 а, скорость v частицы относительно неподвижной системы имеет модуль, равный 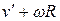 '. Обозначим через
'. Обозначим через 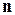 – нормаль к скорости, направленной вдоль нити. Поэтому ускорение частицы в неподвижной системе равно
– нормаль к скорости, направленной вдоль нити. Поэтому ускорение частицы в неподвижной системе равно
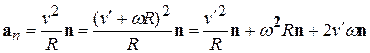 (10.8)
(10.8)
Здесь 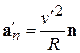 – ускорение частицы относительно диска, т.е. во вращающейся системе отсчета.
– ускорение частицы относительно диска, т.е. во вращающейся системе отсчета.
Умножим левую и правую части выражения (10.8) на массу частицы m. В силу предыдущего обозначения ускорения получим
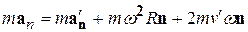 (10.9)
(10.9)
Очевидно, первое выражение в (10.9) есть сила натяжения нити F. Отсюда
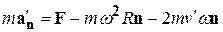 (10.10)
(10.10)
Из формулы (10.10) следует, что наблюдатель, «живущий» на диске, должен заключить, что кроме «реальной» силы F на частицу действуют две дополнительные силы, направленные от оси вращения. Первая из них – центробежная сила инерции. Сила, определяемая по последнему выражению (10.10), и есть сила Кориолиса Fk. С учетом направления сил и векторов физических величин, входящих в формулу этой силы, ее можно представить в виде
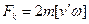 (10.11)
(10.11)
Мы получили формулу (10.11) для случая, когда скорость частицы направлена по касательной к окружности с центром на оси вращения системы К'. Можно показать, что эта формула определяет силу Кориолиса при любом направлении скорости v' по отношению к оси вращения. Из формулы следует, что в случае, когда частица движется в неинерциальной системе параллельно оси вращения (v' коллинеарна с 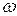 ), сила Кориолиса не возникает.
), сила Кориолиса не возникает.
Из формулы (10.11) вытекает, что:
1) сила Кориолиса перпендикулярна вектору 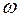 , т.е. всегда лежит в плоскости, перпендикулярной оси вращения системы отсчета;
, т.е. всегда лежит в плоскости, перпендикулярной оси вращения системы отсчета;
2) сила Кориолиса перпендикулярна скорости v' и, следовательно, работы над частицей не совершает. Эта сила может изменить только направление скорости v', но не ее модуль.
Сила Кориолиса действует на тела, движущиеся относительно вращающейся системы отсчета, например, относительно земли. Поэтому действием этих сил объясняется ряд наблюдаемых на земле явлений. В частности, на рис. 10.7 показано воздействие, которое оказывает сила Кориолиса на движение тел вблизи земной поверхности. При свободном падении сила Кориолиса отклоняет тела к востоку. Это отклонение пропорционально синусу широты местности и, следовательно, максимально на экваторе и равно нулю на полюсах. При падении на экваторе с высоты 30 м (примерно такова высота десятиэтажного дома) отклонение составляет 3,6 мм.
Силу Кориолиса необходимо учитывать при стрельбе на дальние расстояния и вводить соответствующую поправку. При выстреле из орудия, направленного на север, снаряд будет отклоняться к востоку в северном полушарии и к западу – в южном (рис. 10.7б). При выстреле вдоль меридиана на юг направления отклонения будут противоположными. При стрельбе вдоль экватора сила Кориолиса приподнимает снаряд кверху, если выстрел произведен в направлении на восток, и прижимает снаряд к Земле, если выстрел произведен в западном направлении (рис. 10.7а).
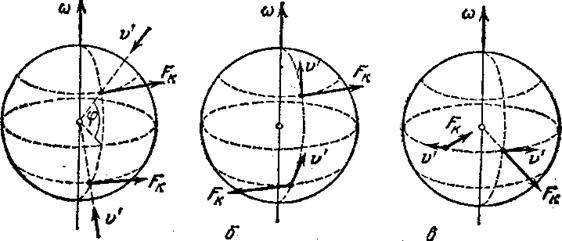
| Рис. 10.7. Влияние силы Кориолиса на движение тел вблизи земной поверхности |
На рис. 10.7б видно, что сила Кориолиса, действующая на тело, движущееся вдоль меридиана в любом направлении (на север или на юг), направлена по отношению к направлению движения вправо в северном полушарии и влево в южном полушарии. Это приводит к тому, что у рек подмывается всегда правый берег в северном полушарии и левый берег в южном полушарии. Действием силы Кориолиса объясняется также неодинаковый износ рельсов при двухколейном движении – в северном полушарии сильнее изнашивается правый рельс, в южном полушарии – левый. Убедительным доказательством суточного вращения Земли является вызываемый действием силы Кориолиса поворот плоскости колебаний маятника. Соответствующий опыт был впервые осуществлен Фуко в 1851 г. в Париже с маятником длиной 67 м. Маятники, предназначенные для демонстрации вращения Земли, называются маятниками Фуко. Такой маятник длиной 98 м имеется в Ленинграде в Исаакиевском соборе.
На рис. 10.8 показан маятник, находящийся на Северном полюсе. Сила Кориолиса все время направлена вправо по ходу маятника (на южном полюсе она направлена влево). Плоскость качаний маятника поворачивается относительно Земли по часовой стрелке, совершая за сутки один оборот. Относительно гелиоцентрической системы отсчета плоскость качаний неподвижна, а Земля поворачивается против часовой стрелки, делая за сутки один оборот.
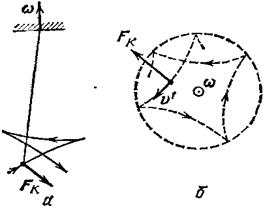
| Рис.10.8. Качание маятника, находящегося на Северном полюсе: a – общий вид; б – траектория груза маятника (вид сверху). Стрелка показывает направление поворота плоскости качаний маятника относительно Земли; вектор 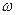 – угловая скорость Земли, v' – скорость груза маятника относительно Земли – угловая скорость Земли, v' – скорость груза маятника относительно Земли
|
Можно показать, что на широте 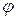 плоскость качаний маятника поворачивается за сутки на угол
плоскость качаний маятника поворачивается за сутки на угол 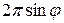 . На экваторе сила Кориолиса направлена вдоль подвеса маятника и не может вызвать поворота плоскости качаний.
. На экваторе сила Кориолиса направлена вдоль подвеса маятника и не может вызвать поворота плоскости качаний.
Контрольные вопросы
1. Когда и почему необходимо рассматривать силы инерции?
2. Что такое силы инерции? Чем они отличаются от сил, действующих в инерциальных системах отсчета?
3. Как направлены центробежная сила инерции и сила Кориолиса? Когда они проявляются? От чего зависят?
4. Как изменится модуль центробежной силы инерции, если скорость вращения системы отсчета увеличить в n раз?
5. Может ли сила Кориолиса изменить скорость частицы?
6. Чему равна сила Кориолиса в случае, когда скорость частицы параллельна оси вращения системы отсчета?
7. В северном полушарии производится выстрел вдоль меридиана на север. Как скажется на движении снаряда суточное вращение Земли?
8. Почему пассажир, стоящий у правой (по ходу поезда) двери движущегося вагона метро, при его повороте оказался прижатым к двери?
Лекция №11. Механические колебания и волны
1. Гармонические колебания и их характеристики
Колебанияминазываются движения или процессы, которые характеризуются определенной повторяемостью во времени. Если этот процесс совершается через равные промежутки времени, то колебание называется периодическим. Наглядным примером такого колебания может служить движение часового механизма.
Колебательные процессы широко распространены в природе и технике. Вибрация натянутой струны, движение поршня дизеля, суточные и годичные изменения температуры воздуха, морские приливы и отливы, волнение водной поверхности, биение сердца, дыхание, тепловое движение ионов кристаллической решетки твердого тела, качание маятника часов, переменный электрический ток и т.д. – все это в конечном счете колебательные процессы. При колебательном движении маятника изменяется координата его центра масс, в случае переменного тока колеблются напряжение и ток в цепи. Физическая природа колебаний может быть разной, поэтому различают колебания механические, электромагнитные и др. Однако различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями. Отсюда следует целесообразность единого подхода к изучению колебаний различной физической природы. Например, единый подход к изучению механических и электромагнитных колебаний применялся английским физиком Д.У.Рэлеем (1842–1919), А.Г.Столетовым, русским инженером-экспериментатором П.Н.Лебедевым (1866–1912). Большой вклад в развитие теории колебаний внесли советский физик Л. И. Мандельштам (1879–1944) и его ученики.
Простейшим типом колебаний являются гармонические колебания– колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Рассмотрение гармонических колебаний важно по двум причинам: 1) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому; 2) различные периодические процессыможно представить как наложение гармонических колебаний.
С основными закономерностями и характеристиками гармонического колебания проще всего познакомиться на примере равномерного движения материальной точки по окружности. Пусть материальная точка М движется по часовой стрелке по окружности радиусом ОМ=А с постоянной угловой скоростью 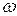 (рис.11.1) .
(рис.11.1) .
Тогда ее проекция N на горизонтальный диаметр будет совершать периодические колебания около положения равновесия О, а величина смещения этой проекции – изменяться в пределах от +А до – А, также совершая периодические колебания. Величина смещения в любой момент времени определяется очевидным соотношением
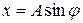 (11.1)
(11.1)
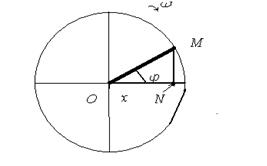
| Рис.11.1 |
Из определения угловой скорости следует, что 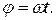
Тогда формулу (11.1) можно написать в виде
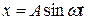 (11.2)
(11.2)
Если точка М проецируется на вертикальный диаметр, колеблющаяся величина х изменяется со временем по закону косинуса:
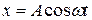 (11.3)
(11.3)
В общем случае гармонические колебания величины х описываются уравнением типа
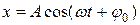 (11.4)
(11.4)
где А – максимальное значение колеблющейся величины, называемое амплитудой колебаний, 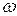 – круговая (циклическая) частота,
– круговая (циклическая) частота, 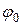 – начальная фаза колебаний в момент времени
– начальная фаза колебаний в момент времени 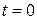 ,
, 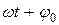 – фаза колебанийв момент времени t.
– фаза колебанийв момент времени t.
Колебанияназываются свободными(или собственными),если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему (систему, совершающую колебания). Для этих колебаний циклическую частоту обозначим как .
Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемый периодом колебания.За это время фаза колебания получает приращение 2л, т.е. 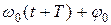 =
= 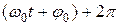 , откуда
, откуда
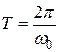 (11.5)
(11.5)
Величина, обратная периоду колебаний,
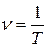 (11.6)
(11.6)
т.е.число полных колебаний, совершаемых в единицу времени, называется частотой колебаний.Сравнивая (11.5) и (11.6), получим 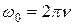 .
.
Единица частоты – герц(Гц): 1 Гц – частота периодического процесса, при которой за 1с совершается один цикл процесса.
Запишем первую и вторую производные по времени от гармонически колеблющейся величины s (соответственно скорость и ускорение):
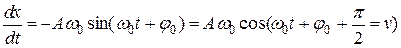 , (11.7)
, (11.7)
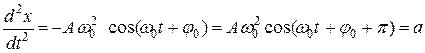 , (11.8)
, (11.8)
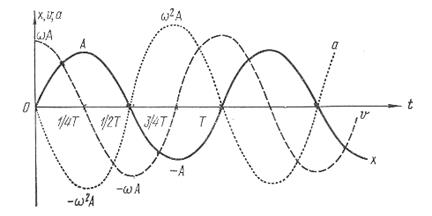
т.е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин (11.7) и (11.8) соответственно равны 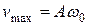 и
и 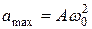 . Фаза скорости (11.7) отличается от фазы величины (11.1) на
. Фаза скорости (11.7) отличается от фазы величины (11.1) на  , а фаза ускорения (11.8) отличается от фазы величины (11.1) на л. Следовательно,
, а фаза ускорения (11.8) отличается от фазы величины (11.1) на л. Следовательно,
– в моменты времени, когда х = 0, v приобретает наибольшие значения;
– когда же х достигает максимального отрицательного значения, то a приобретает наибольшее положительное значение (рис. 11.2).
| Рис.11.1 |
Из выражения (11.8) следует дифференциальное уравнение гармонических колебаний
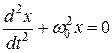 (11.9)
(11.9)
Решением этого уравнения являются выражения (11.1), (11.3) или (11.4).
2. Динамика колебательного движения
Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси координат х около положения равновесия, принятого за начало координат. Тогда зависимость координаты х от времени t задается, например, формулой 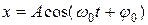 .
.
В этом случае, как видно из формулы (11.8), при колебательном движении ускорение переменно. Следовательно, движение обусловлено действием переменной силы. Пусть под действием переменной силы 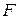 материальная точка массой m совершает гармоническое колебание с ускорением а. Тогда,
материальная точка массой m совершает гармоническое колебание с ускорением а. Тогда, 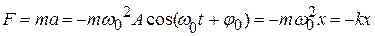 , так как
, так как 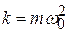 .
.
Следовательно, сила пропорциональна смещению материальной точки из положения равновесия и направлена в противоположную сторону (к положению равновесия). Эта сила стремится возвратить точку в положение равновесия, поэтому ее называют возвращающей силой. Возвращающей силой может быть, например, сила упругости, так как она тоже пропорциональна смещению и противоположна ему по знаку. Возвращающие силы могут иметь не только упругую, но и другую природу. В таких случаях они называются квазиупругими силами.
Кинетическая энергия материальной точки, совершающей прямолинейные гармонические колебания, равна
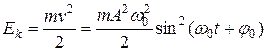 (11.10)
(11.10)
или 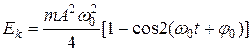 (11.11)
(11.11)
Потенциальная энергия материальнойточки, совершающей гармонические колебания под действием упругой силы F, равна
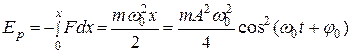 (11.12)
(11.12)
или 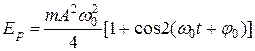 (11.13)
(11.13)
Сложив (11.11) и (11.13), получим формулу для полной энергии:
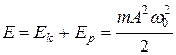 (11.14)
(11.14)
Полная энергия остается постоянной, так как при гармонических колебаниях справедлив закон сохранения механической энергии, поскольку упругая сила консервативна.
Из формул (11.11) и (11.13) следует, что 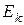 и
и  изменяются с частотой
изменяются с частотой 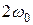 , т.е. с частотой, которая в два раза превышает частоту гармонического колебания.
, т.е. с частотой, которая в два раза превышает частоту гармонического колебания.
На рис. 11.3 представлены графики зависимости х, Ек =Т и Ер =II от времени. Так как средние значения <sin2a> = <cos2a> =1/2, то из формул (11.11), (11.13) и (11.14) следует, что средние значения 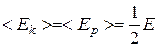 .
.
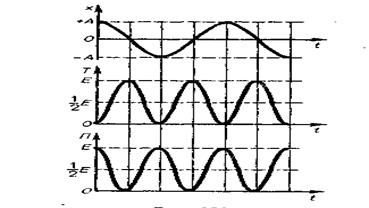
| Рис.11.3 |
3. Гармонический осциллятор. Пружинный, физический
и математический маятники
Гармоническим осцилляторомназывается система, совершающая колебания, описываемые уравнением вида
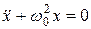 (11.15)
(11.15)
Колебания гармонического осциллятора являются важным примером периодического движения и служат точной или приближенной моделью во многих задачах классической и квантовой физики. Примерами гармонического осциллятора являются пружинный, физический и математический маятники, колебательный контур.
1. Пружинный маятник –это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы 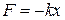 ,где k – коэффициент упругости, в случае пружины называемый жесткостью.
,где k – коэффициент упругости, в случае пружины называемый жесткостью.
Уравнение движения маятника 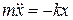 или
или 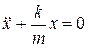
Из его решения следует, что пружинный маятник совершает гармонические колебания по закону 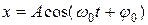 с циклической частотой
с циклической частотой
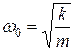 (11.16)
(11.16)
Дата добавления: 2015-08-08; просмотров: 1139;
