Колебания, возникающие под действием внешней периодически изменяющейся силы, называются вынужденными механическими колебаниями. 4 страница
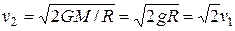 (12.14)
(12.14)
Учитывая значение  ,получим, что
,получим, что 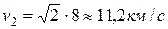 .
.
Заметим, что значение 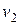 не зависит от направления, в котором запускается тело с Земли. От этого направления зависит лишь вид траектории, по которой тело удаляется от Земли.
не зависит от направления, в котором запускается тело с Земли. От этого направления зависит лишь вид траектории, по которой тело удаляется от Земли.
Третьей космической скоростью 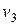 называют скорость, которую необходимо сообщить телу на Земле, чтобы оно покинуло пределы Солнечной системы, преодолев притяжение Солнца.
называют скорость, которую необходимо сообщить телу на Земле, чтобы оно покинуло пределы Солнечной системы, преодолев притяжение Солнца.
Подставив в формулу (12.14) вместо M массу Солнца ( 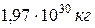 ) и вместо R – радиус земной орбиты
) и вместо R – радиус земной орбиты 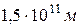 , получим значение скорости, равное 42 км/с. Такова была бы третья космическая скорость, если бы Земля в момент запуска была неподвижна и не притягивала бы тело к себе. Но Земля сама движется относительно Солнца со скоростью 30 км/с. Поэтому при запуске в направлении орбитального движения Земли скорость 42 км/с относительно Солнца достигается при скорости относительно Земли, равной 42-30=12 км/с, а при запуске в противоположном направлении 42+30 км/с = 72 км/с. Таковы были бы минимальное и максимальное значения
, получим значение скорости, равное 42 км/с. Такова была бы третья космическая скорость, если бы Земля в момент запуска была неподвижна и не притягивала бы тело к себе. Но Земля сама движется относительно Солнца со скоростью 30 км/с. Поэтому при запуске в направлении орбитального движения Земли скорость 42 км/с относительно Солнца достигается при скорости относительно Земли, равной 42-30=12 км/с, а при запуске в противоположном направлении 42+30 км/с = 72 км/с. Таковы были бы минимальное и максимальное значения 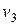 ,если бы не было бы притяжения тела к Земле. С учетом этого притяжения для третьей космической скорости получаются значения от 17 до 73 км/с. Сообщение телам таких больших начальных скоростей является сложной технической задачей. Ее первое теоретическое осуществление начато К. Э. Циолковским, им была выведена уже рассмотренная нами формула Циолковского, позволяющая рассчитывать скорость ракет.
,если бы не было бы притяжения тела к Земле. С учетом этого притяжения для третьей космической скорости получаются значения от 17 до 73 км/с. Сообщение телам таких больших начальных скоростей является сложной технической задачей. Ее первое теоретическое осуществление начато К. Э. Циолковским, им была выведена уже рассмотренная нами формула Циолковского, позволяющая рассчитывать скорость ракет.
Впервые космические скорости были достигнуты в СССР: первая – при запуске первого искусственного спутника Земли в 1957 г., вторая – при запуске ракеты в 1959 г. После исторического полета Ю.А.Гагарина в 1961 г. начинается бурное развитие как советской, так и зарубежной космонавтики.
6. Принцип эквивалентности гравитационных сил и сил инерции
Мы уже неоднократно отмечали, что все тела, независимо от их массы и химического состава, получают в данном гравитационном поле одинаковые ускорения. Поэтому в таком поле они движутся совершенно одинаково, если только одинаковы начальные условия. Тем же свойством обладают свободно движущиеся тела, если их движение рассматривать относительно какой-либо неинерциальной системы отсчета. Иначе говоря, указанным свойством обладают также силы инерции. Эта аналогия между силами тяготения и силами инерции явилась отправной точкой при построении общей теории относительности, или релятивистской теории гравитации Эйнштейна.
Рассмотрим по примеру Эйнштейна, что происходит в движущемся лифте. Допустим сначала, что лифт неподвижно висит на тросе или движется равномерно относительно Земли. Все тела в лифте подвергаются действию земного поля тяготения. Пассажир в лифте ощущает вес собственного тела, оказывает давление на пол лифта, подвергается со стороны пола равному и противоположно направленному противодавлению. Груз, подвешенный на пружине, растягивает ее силою своего веса. Все тела, предоставленные самим себе, свободно падают относительно лифта с одним и тем же ускорением gи т.д.
Вообразим теперь, что лифт настолько удален от Земли и прочих небесных тел, что он практически не подвергается с их стороны никаким гравитационным воздействиям. Пусть кто-то тянет за трос лифта, сообщая последнему постоянное ускорение а = - g. Гравитационного поля в лифте нет, зато есть сила инерции -та = mg. Под действием таких сил все тела в лифте, если их ничем не удерживать, начнут «падать» с прежним ускорением g. Груз, подвешенный на пружине, растянет ее, как если бы он обладал весом mg. Пассажир в лифте будет оказывать на пол такое же давление, как и в предыдущем случае. Короче говоря, все механические явления и движения в лифте будут в точности такими же, что и в неподвижном лифте, висящем в поле тяжести. Эйнштейн распространил это утверждение не только на механические, но и на любые физические явления. Для такой гипотезы имеются веские основания. В природе нет чисто механических явлений. В основе каждого «механического» явления лежит громадное множество разнообразных других явлений, относящихся к различным разделам физики. Так, столкновение бильярдных шаров обычно рассматривают как типично механическое явление. Но существование самих шаров и их внутренняя структура определяются квантовыми законами, а упругие силы, развивающиеся во время столкновения, сводятся к силам электростатического взаимодействия заряженных частиц, из которых построены тела.
Итак, все физические явления в равномерно ускоренном лифте будут происходить в точности так же, как и в неподвижном лифте, висящем в однородном поле тяжести. Между тем дорелятивистская физика рассматривала оба случая как существенно разные. В первом случае явления объяснялись действием гравитационного поля, во втором – действием сил инерции. В первом случае лифт является инерциальной системой отсчета, в которой есть однородное поле тяготения. Во втором случае поля тяготения нет, зато есть силы инерции, так как лифт является неинерциальной системой отсчета.
Если лифт в однородном поле тяжести движется вверх или вниз с ускорением а, то на тело в лифте действует сила тяжести mgи сила инерции -та. Результирующая сила т (g - а) состоит из этих двух слагаемых, совершенно различных по своей физической природе. Между тем все явления внутри лифта будут происходить так, как если бы в нем действовало однородное гравитационное поле с напряженностью g' = g - а. Вчастности, когда лифт падает свободно, g'= 0, т.е. наступает «состояние невесомости». Допустим, что пассажир в лифте имеет возможность производить опыты только над телами внутри лифта и лишен возможности наблюдать внешний мир. Замечая, что все тела падают в лифте с одним и тем же ускорением, он не может на основании одного только этого факта решить, чем вызвано это ускорение: однородным гравитационным полем, ускоренным поступательным движением самого лифта, или, наконец, и тем, и другим. Никакие опыты по свободному падению тел в лифте не могут отделить однородное гравитационное поле от однородного поля сил инерции. По предположению Эйнштейна это невозможно сделать и с помощью любых физических опытов. Это предположение Эйнштейн возвел в постулат и выдвинул принцип эквивалентности гравитационных сил и сил инерции.
Согласно этому принципу все физические явления в гравитационном поле происходят совершенно так же, как и в соответствующем поле сил инерции, если напряженности обоих полей в соответствующих точках пространства совпадают, а начальные условия одинаковы для всех тел замкнутой системы.
Принцип эквивалентности вовсе не утверждает, что всякое гравитационное поле может быть имитировано силами инерции, т.е. создано надлежащим ускоренным движением системы отсчета. Он не утверждает также, что любые силы инерции во всем пространстве можно заменить гравитационными. Оба эти утверждения верны, вообще говоря, только для однородных полей, т.е. таких полей, напряженность которых одна и та же во всех точках пространства.
Контрольные вопросы
1. Перечислите законы Кеплера. В чем значение этих законов?
2. При соблюдении каких условий справедлив закон всемирного тяготения?
3. Как определяется гравитационная постоянная и каков ее физический смысл?
4. Что такое гравитационная масса?
5. Что такое напряженность поля тяготения?
6. Какое поле тяготения называется однородным? центральным?
7. Какие величины вводятся для характеристики поля тяготения и какова связь между ними? Дайте их определения.
8. Известно, что сила тяготения пропорциональна массе тела. Почему же тяжелое тело не падает быстрее легкого?
9. Покажите, что силы тяготения консервативны.
10. Чему равно максимальное значение потенциальной энергии системы из двух тел, находящихся в поле тяготения? Когда оно достигается?
11. Какие траектории движения имеют спутники, получившие первую и вторую космическую скорости?
12. Как вычисляются первая, вторая и третья космическая скорости?
13. Каковы достижения в области освоения и исследования космического пространства?
14. Сформулируйте принцип эквивалентности Эйнштейна.
Лекция № 13. Элементы специальной теории относительности
1. Преобразования Галилея. Механический принцип относительности
Если системы отсчета движутся относительно друг друга равномерно и прямолинейно и в одной из них справедливы законы динамики Ньютона, то эти системы являются инерциальными. Установлено также, что во всех инерциальных системах отсчета законы классической динамики имеют одинаковую форму; в этом суть механического принципа относительности(принципа относительности Галилея).
Для его доказательства рассмотрим две системы отсчета: инерциальную систему К (с координатами х, у, z), которую условно будем считать неподвижной, и систему 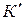 (с координатами х', у', z'), движущуюся относительно К равномерно и прямолинейно со скоростью
(с координатами х', у', z'), движущуюся относительно К равномерно и прямолинейно со скоростью 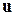 (
( 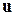 = const). Отсчет времени начнем с момента, когда начала координат обеих систем совпадают. Пусть в произвольный момент времени t расположение этих систем друг относительно друга имеет вид, изображенный на рис. 58. Скорость
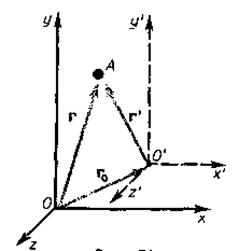
= const). Отсчет времени начнем с момента, когда начала координат обеих систем совпадают. Пусть в произвольный момент времени t расположение этих систем друг относительно друга имеет вид, изображенный на рис. 58. Скорость 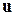 направлена вдоль ОО', радиус-вектор, проведенный из О в О',
направлена вдоль ОО', радиус-вектор, проведенный из О в О', 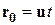 .
.
| Рис. 13.1 |
Найдем связь между координатами произвольной точки А в обеих системах. Из рис. 13.1 видно, что
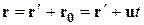 (13.1)
(13.1)
Уравнение (13.1) можно записать в проекциях на оси координат:
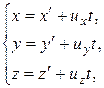 (13.2)
(13.2)
 Уравнения (13.1) и (13.2) носят название преобразований координат Галилея.
Уравнения (13.1) и (13.2) носят название преобразований координат Галилея.
В частном случае, когда система К' движется со скоростью 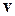 вдоль положительного направления оси х системы К (в начальный момент времени оси координат совпадают), преобразовании координат Галилея имеют вид
вдоль положительного направления оси х системы К (в начальный момент времени оси координат совпадают), преобразовании координат Галилея имеют вид
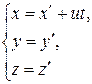
В классической механике предполагается, что ход времени не зависит от относительного движения систем отсчета, т.е. к преобразованиям (13.2) можно добавить еще одно уравнение:
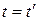 (13.3)
(13.3)
Записанные соотношения справедливы лишь в случае классической механики ( 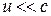 ), а при скоростях, сравнимых со скоростью света, преобразования Галилея заменяются более общими преобразованиями Лоренца (X. Лоренц (1853–1928) – нидерландский физик-теоретик).
), а при скоростях, сравнимых со скоростью света, преобразования Галилея заменяются более общими преобразованиями Лоренца (X. Лоренц (1853–1928) – нидерландский физик-теоретик).
Продифференцировав выражение (13.1) по времени (с учетом (13.3)), получим уравнение

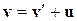 ,(13.4)
,(13.4)
которое представляет собой правило сложения скоростей в классической механике.
Ускорение в системе отсчета К 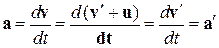
Таким образом, ускорение точки А в системах отсчета K и К', движущихся относительно друг друга равномерно и прямолинейно, одинаково:
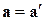 . (13.5)
. (13.5)
Следовательно, если на точку А другие тела не действуют ( 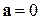 ), то согласно (13.5) и
), то согласно (13.5) и 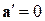 система К' является инерциальной (точка движется относительно нее равномерно и прямолинейно или покоится).
система К' является инерциальной (точка движется относительно нее равномерно и прямолинейно или покоится).
Таким образом, из соотношения (13.5) вытекает доказательство механического принципа относительности: уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяются, т.е. являются инвариантнымипо отношению к преобразованиям координат. Галилей обратил внимание, что никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя установить, покоится ли она или движется равномерно и прямолинейно. Например, сидя в каюте корабля, движущегося равномерно и прямолинейно, мы не можем определить, покоится корабль или движется, не выглянув в окно.
2. Постулаты специальной (частной) теории относительности
Классическая механика Ньютона прекрасно описывает движение макротел, движущихся с малыми скоростями ( 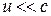 ). Однако в конце XIX в. выяснилось, что выводы классической механики противоречат некоторым опытным данным, в частности при изучении движения быстрых заряженных частиц оказалось, что их движение не подчиняется законам механики. Далее возникли затруднения при попытках применить механику Ньютона к объяснению распространения света. Если источник и приемник света движутся относительно друг друга равномерно и прямолинейно, то, согласно классической механике, измеренная скорость должна зависеть от относительной скорости их движения. Американский физик А. Майкельсон (1852–1913) в своем знаменитом опыте в 1881 г., а затем в 1887 г. совместно с E. Морли (американский физик, 1838–1923) – опыт Майкельсона-Морли –пытался обнаружить движение Земли относительно эфира (эфирный ветер), применяя интерферометр Майкельсона. Обнаружить эфирный ветер Майкельсону не удалось, как, впрочем, не удалось его обнаружить и в других многочисленных опытах. Опыты «упрямо» показывали, что скорости света в двух движущихся относительно друг друга системах равны. Это противоречило правилу сложения скоростей классической механики.
). Однако в конце XIX в. выяснилось, что выводы классической механики противоречат некоторым опытным данным, в частности при изучении движения быстрых заряженных частиц оказалось, что их движение не подчиняется законам механики. Далее возникли затруднения при попытках применить механику Ньютона к объяснению распространения света. Если источник и приемник света движутся относительно друг друга равномерно и прямолинейно, то, согласно классической механике, измеренная скорость должна зависеть от относительной скорости их движения. Американский физик А. Майкельсон (1852–1913) в своем знаменитом опыте в 1881 г., а затем в 1887 г. совместно с E. Морли (американский физик, 1838–1923) – опыт Майкельсона-Морли –пытался обнаружить движение Земли относительно эфира (эфирный ветер), применяя интерферометр Майкельсона. Обнаружить эфирный ветер Майкельсону не удалось, как, впрочем, не удалось его обнаружить и в других многочисленных опытах. Опыты «упрямо» показывали, что скорости света в двух движущихся относительно друг друга системах равны. Это противоречило правилу сложения скоростей классической механики.
Одновременно было показано противоречие между классической теорией и уравнениями Дж. К. Максвелла (английский физик, 1831–1879), лежащими в основе понимания света как электромагнитной волны.
Для объяснения этих и некоторых других опытных данных необходимо было создать новую механику, которая, объясняя эти факты, содержала бы ньютоновскую механику как предельный случай для малых скоростей ( 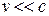 ). Это удалось сделать А. Эйнштейну, одному из основателей современной физики. А. Эйнштейн пришел к выводу о том, что мирового эфира – особой среды, которая могла бы быть принята в качестве абсолютной системы, – не существует. Существование постоянной скорости распространения света в вакууме находилось в согласии с уравнениями Максвелла.
). Это удалось сделать А. Эйнштейну, одному из основателей современной физики. А. Эйнштейн пришел к выводу о том, что мирового эфира – особой среды, которая могла бы быть принята в качестве абсолютной системы, – не существует. Существование постоянной скорости распространения света в вакууме находилось в согласии с уравнениями Максвелла.
Таким образом, А. Эйнштейн заложил основы специальной теории относительности.Эта теория представляет собой современную физическую теорию пространства и времени, в которой, как и в классической ньютоновской механике, предполагается, что время однородно, а пространство однородно и изотропно. Специальная теория относительности часто называется также релятивистской теорией,а специфические явления, описываемые этой теорией,– релятивистскими эффектами.
В основе специальной теории относительности лежат постулаты Эйнштейна,сформулированные им в 1905 г.
I. Принцип относительности:никакие опыты (механические, электрические, оптические), проведенные внутри данной инерциальной системы отсчета, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно; все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой.
II. Принцип инвариантности скорости света:скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальнык системах отсчета.
Первый постулат Эйнштейна, являясь обобщением механического принципа относительности Галилея на любые физические процессы, утверждает, таким образом, что физические законы инвариантны по отношению к выбору инерциальной системы отсчета, а уравнения, описывающие эти законы, одинаковы по форме во всех инерциальных системах отсчета. Согласно этому постулату все инерциальные системы отсчета совершенно равноправны, т.е. явления (механические, электродинамические, оптические и др.) во всех инерциальных системах отсчета протекают одинаково.
Согласно второму постулату Эйнштейна постоянство скорости света – фундаментальное свойство природы, которое констатируется как опытный факт.
Специальная теория относительности потребовала отказа от привычных представлений о пространстве и времени, принятых в классической механике, поскольку они противоречили принципу постоянства скорости света. Потеряло смысл не только абсолютное пространство, но и абсолютное время.
Постулаты Эйнштейна и теория, построенная на их основе, установили новый взгляд на мир и новые пространственно-временные представления, например такие, как относительность длин и промежутков времени, относительность одновременности событий. Эти и другие следствия из теории Эйнштейна находят надежное экспериментальное подтверждение, являясь тем самым обоснованием постулатов Эйнштейна – обоснованием специальной теории относительности.
3. Преобразования Лоренца
Анализ явлений в инерциальных системах отсчета, проведенный А. Эйнштейном на основе сформулированных им постулатов, показал, что классические преобразования Галилея несовместимы с ними и, следовательно, должны быть заменены преобразованиями, удовлетворяющими постулатам теории относительности.
Для иллюстрации этого вывода рассмотрим две инерциальные системы отсчета: К (с координатами х, у, z) и К' (с координатами х', у', z'), движущуюся относительно К (вдоль оси х) со скоростью v = const (рис.13.2). Пусть в начальный момент времени t = t' = 0, когда начала координат О и О' совпадают, излучается световой импульс. Согласно второму постулату Эйнштейна, скорость света в обеих системах одна и та же и равна с. Поэтому если за время t в системе К' сигнал дойдет до некоторой точки А (рис. 13.2), пройдя расстояние
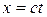 , (13.6)
, (13.6)
то в системе К' координата светового импульса в момент достижения точки А
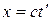 (13.7)
(13.7)
где 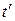 – время прохождения светового импульса от начала координат до точки А в системе К'. Вычитая (13.6) из (13.7), получим
– время прохождения светового импульса от начала координат до точки А в системе К'. Вычитая (13.6) из (13.7), получим 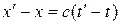 .
.
| Рис.13.2 |
Так как 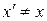 (система К' перемещается по отношению к системе К), то
(система К' перемещается по отношению к системе К), то 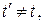 т.е. отсчет времени в системах K и К' различен – отсчет времени имеет относительный характер (в классической физике считается, что время во всех инерциальных системах отсчета течет одинаково, т.е.
т.е. отсчет времени в системах K и К' различен – отсчет времени имеет относительный характер (в классической физике считается, что время во всех инерциальных системах отсчета течет одинаково, т.е. 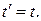 ).
).
Эйнштейн показал, что в теории относительности классические преобразования Галилея, описывающие переход от одной инерциальной системы отсчета к другой, заменяются преобразованиями Лоренца, удовлетворяющими постулатам Эйнштейна (формулы представлены для случая, когда К' движется относительно К со скоростью v вдоль оси x).
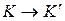
| 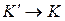
|
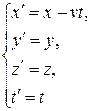
| 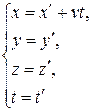
|
Эти преобразования предложены Лоренцом в 1904 г. еще до появления теории относительности как преобразования, относительно которых уравнения Максвелла инвариантны.
Преобразования Лоренцаимеют вид
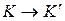
| 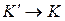
|
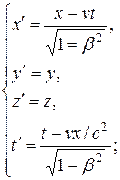
| 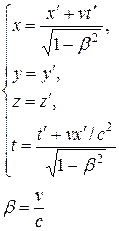 (13.8) (13.8)
|
Из сравнения приведенных уравнений вытекает, что они симметричны и отличаются лишь знаком при v. Это очевидно, так как если скорость движения системы 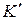 относительно системы K равна v, то скорость движения К относительно К' равна v.
относительно системы K равна v, то скорость движения К относительно К' равна v.
Из преобразований Лоренца вытекает также, что при малых скоростях (по сравнению со скоростью света), т.е. когда 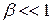 , они переходят в классические преобразования Галилея (в этом заключается суть принципа соответствия),которые являются, следовательно, предельным случаем преобразований Лоренца. При v>c выражения (13.8) для х, t, x', t' теряют физический смысл (становятся мнимыми). Это находится, в свою очередь, в соответствии с тем, что движение со скоростью, большей скорости света в вакууме, невозможно.
, они переходят в классические преобразования Галилея (в этом заключается суть принципа соответствия),которые являются, следовательно, предельным случаем преобразований Лоренца. При v>c выражения (13.8) для х, t, x', t' теряют физический смысл (становятся мнимыми). Это находится, в свою очередь, в соответствии с тем, что движение со скоростью, большей скорости света в вакууме, невозможно.
Из преобразований Лоренца следует очень важный вывод о том, что как расстояние, так и промежуток времени между двумя событиями меняются при переходе от одной инерциальной системы отсчета к другой, в то время как в рамках преобразований Галилея эти величины считались абсолютными, не изменяющимися при переходе от системы к системе. Кроме того, как пространственные, так и временные преобразования (см. (13.8)) не являются независимыми, поскольку в закон преобразования координат входит время, а в закон преобразования времени – пространственные координаты, т.е. устанавливается взаимосвязь пространства и времени. Таким образом, теория Эйнштейна оперирует не с трехмерным пространством, к которому присоединяется понятие времени, а рассматривает неразрывно связанные пространственные и временные координаты, образующие четырехмерное пространство – время.
4. Следствия из преобразований Лоренца
1. Одновременность событий в разных системах отсчета.Пусть в системе К в точках с координатами 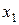 и
и 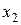 dмоменты времени
dмоменты времени 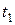 и
и 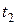 происходят два события.
происходят два события.
В системе 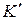 им соответствуют координаты
им соответствуют координаты 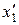 и
и 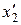 и моменты времени
и моменты времени 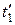 и
и 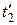 . Если события в системе К происходят в одной точке (
. Если события в системе К происходят в одной точке ( 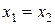 ) и являются одновременными(
) и являются одновременными( 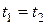 ), то, согласно преобразованиям Лоренца (13.8),
), то, согласно преобразованиям Лоренца (13.8), 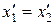 и
и 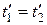 , т.е. эти события являются одновременными и пространственно совпадающими для любой инерциальной системы отсчета.
, т.е. эти события являются одновременными и пространственно совпадающими для любой инерциальной системы отсчета.
Если события в системе К пространственно разобщены 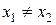 , но одновременны (
, но одновременны ( 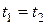 ), то в системе К', согласно преобразованиям Лоренца (13.8),
), то в системе К', согласно преобразованиям Лоренца (13.8), 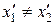 ,
, 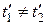 .
.
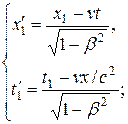
| 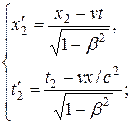
|
Таким образом, в системе К' эти события, оставаясь пространственно разобщенными, оказываются и неодновременными. Знак разности 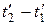 определяется знаком выражения
определяется знаком выражения 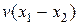 , поэтому в различных точках системы отсчета К' (при разных v) разность
, поэтому в различных точках системы отсчета К' (при разных v) разность 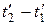 будет различной по величине и может отличаться по знаку. Следовательно, в одних системах отсчета первое событие может предшествовать второму, в то время как в других системах отсчета наоборот второе событие предшествует первому. Сказанное, однако, не относится к причинно-следственным событиям, так как можно показать, что порядок следования причинно-следственных событий одинаков во всех инерциальных системах отсчета.
будет различной по величине и может отличаться по знаку. Следовательно, в одних системах отсчета первое событие может предшествовать второму, в то время как в других системах отсчета наоборот второе событие предшествует первому. Сказанное, однако, не относится к причинно-следственным событиям, так как можно показать, что порядок следования причинно-следственных событий одинаков во всех инерциальных системах отсчета.
2. Длительность событий в разных системах отсчета.Пусть в некоторой точке (с координатой), покоящейся относительно системы К, происходит событие, длительность которого (разность показаний часов в конце и начале события) 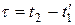 , где индексы 1 и 2 соответствуют началу и концу события. Длительность этого же события в системе
, где индексы 1 и 2 соответствуют началу и концу события. Длительность этого же события в системе
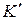
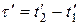 , (13.9)
, (13.9)
причем началу и концу события согласно (13.8) соответствуют
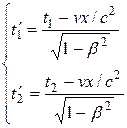 (13.10)
(13.10)
Подставляя (13.10) в (13.9), получим 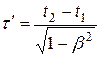
или 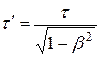 (13.11)
(13.11)
Из соотношения (13.11) вытекает, что 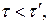 т.е. длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна. Этот результат может быть еще истолкован следующим образом: интервал времени
т.е. длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна. Этот результат может быть еще истолкован следующим образом: интервал времени 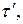 отсчитанный по часам в системе К', с точки зрения наблюдателя в системе К продолжительнее интервала
отсчитанный по часам в системе К', с точки зрения наблюдателя в системе К продолжительнее интервала 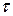 , отсчитанного по его часам. Следовательно, часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов, т.е. ход часов замедляется в системе отсчета, относительно которой часы движутся. На основании относительности понятий «неподвижная» и «движущаяся» системы соотношения для
, отсчитанного по его часам. Следовательно, часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов, т.е. ход часов замедляется в системе отсчета, относительно которой часы движутся. На основании относительности понятий «неподвижная» и «движущаяся» системы соотношения для 
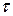 и
и 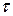 ' обратимы. Из (13.11) следует, что замедление хода часов становится заметным лишь при скоростях, близких к скорости света в вакууме.
' обратимы. Из (13.11) следует, что замедление хода часов становится заметным лишь при скоростях, близких к скорости света в вакууме.
Дата добавления: 2015-08-08; просмотров: 965;

