Колебания, возникающие под действием внешней периодически изменяющейся силы, называются вынужденными механическими колебаниями. 3 страница

Ультразвук применяют для воздействия на различные процессы (кристаллизацию, диффузию, тепло- и массообмен в металлургии и т.д.) и биологические объекты (повышение интенсивности процессов обмена и т.д.), для изучения физических свойств веществ (поглощения, структуры вещества и т.д.). Ультразвук используется также для механической обработки очень твердых и очень хрупких тел, в медицине (диагностика, ультразвуковая хирургия, микромассаж тканей) и т.д.

Контрольные вопросы

1. Что такое колебания? свободные колебания? гармонические колебания? периодические процессы?

2. Дайте определения амплитуды, фазы, периода, частоты, циклической частоты колебания.

3. Какова связь амплитуды и фазы смещения, скорости и ускорения при прямолинейных гармонических колебаниях?

4. Выведите формулы для скорости и ускорения гармонически колеблющейся точки как функции времени.

5. Выведите и прокомментируйте формулы для кинетической, потенциальной и полной энергии при гармонических колебаниях.

6. Чему равно отношение полной энергии гармонического колебания к максимальному значению возвращающей силы, вызывающей это колебание?

7. Как можно сравнить между собой массы тела, измеряя частоты колебаний при подвешивании этих масс к пружине?

8. Что называется гармоническим осциллятором, пружинным, физическим и математическим маятником?

9. Выведите формулы для периодов колебаний пружинного, физического и математического маятников.

10. Что такое приведенная длина физического маятника?

11. 11.Какие процессы происходят при свободных гармонических колебаниях в колебательном контуре? Чем определяется их период?

12. Запишите и проанализируйте дифференциальное уравнение свободных гармонических колебаний в контуре.

13. Что такое биения? Чему равна частота биений? период?

14. Какова траектория точки, участвующей одновременно в двух взаимно перпендикулярных гармонических колебаниях содинаковыми периодами? Когда получается окружность? прямая?

15. Как по виду фигур Лиссажу можно определить отношение частот складываемых колебаний?

16. Запишите дифференциальное уравнение затухающих колебаний и его решение.

17. Как изменяется частота собственных колебаний с увеличением массы колеблющегося тела?

18. По какому закону изменяется амплитуда затухающих колебаний? Являются ли затухающие колебания периодическими?

19. Почему частота затухающих колебаний должна быть меньше частоты собственных колебаний системы?

20. Что такое коэффициент затухания, декремент затухания, логарифмический декремент затухания? В чем заключается физический смысл этих величин?

21. При каких условиях наблюдается апериодическое движение?

22. Что такое автоколебания? В чем их отличие от вынужденных и свободных незатухающих колебаний? Где они применяются?

23. Что такое вынужденные колебания? Запишите дифференциальное уравнение вынужденных колебаний и решите его.

24. От чего зависит амплитуда вынужденных колебаний? Запишите выражение для амплитуды и фазы при резонансе.

25. Нарисуйте, проанализируйте резонансные кривые для амплитуды смещения и скорости. В чем их отличие?

26. Почему добротность является важнейшей характеристикой резонансных свойств системы?

27. Чему равен сдвиг фаз между смещением и вынуждающей силой при резонансе?

28. Что называется резонансом? Какова его роль?

29. Что называется длиной волны? Какова связь между длиной волны, скоростью и периодом?

30. Какая волна является бегущей, гармонической, плоской, сферической? Каковы их уравнения?

31. Что такое волновое число? фазовая и групповая скорости?

32. В чем заключается физический смысл вектора Умова?

33. При каких условиях возникает интерференция волн? Назовите условия интерференционных максимума и минимума.

34. Две волны с одинаковым периодом распространяются в одном направлении. Разность хода равна четному числу полуволн. Что получится в результате интерференции?

35. Две волны, распространяющиеся навстречу друг другу, отличаются только амплитудами. Образуют ли они стоячую волну?

36. Чем стоячая волна отличается от бегущей?

37. Чему равно расстояние между двумя соседними узлами стоячей волны? двумя соседними пучностями? соседними пучностью и узлом?

38. Что такое звуковые волны? Звуковые волны в воздухе продольные или поперечные? Почему?

39. Может ли звук распространяться в вакууме?

40. От чего зависят громкость, высота и тембр звука?

41. Что такое эффект Доплера? Чему будет равна частота колебаний, воспринимаемых покоящимся приемником, если источник колебаний от него удаляется?

42. Какое влияние оказывает скорость ветра на эффект Доплера?

43. Как определить частоту звука, воспринимаемую приемником, если источник звука и приемник движутся?

Лекция №12. Всемирное тяготение

1. Законы Кеплера и закон всемирного тяготения

Еще в глубокой древности было замечено, что в отличие от звезд, которые неизменно сохраняют свое взаимное расположение в пространстве в течение столетий, планеты описывают сложнейшие траектории. Для объяснения петлеобразного движения планет древнегреческий ученый К.Птолемей (II в. н.э.) предположил, что каждая из планет движется по малому кругу (эпициклу), центр которого равномерно движется по большому кругу, в центре которого находится Земля (он считал, что Землю расположена в центре Вселенной). Эта концепция получила название птолемеевой геоцентрической системой мираи при поддержке католической церкви господствовала почти полторы тысячи лет.

В начале XVI в. польским астрономом Н.Коперником (1473–1543) обоснована гелиоцентрическая система, согласно которой движения небесных тел объясняются движением Земли (а также других планет) вокруг Солнца и суточным вращением Земли. Теория и наблюдения Коперника воспринимались как занимательная фантазия.

К началу XVII столетия большинство ученых убедилось в справедливости гелиоцентрической системы мира. И. Кеплер (1571 – 1630), обработав и уточнив результаты многочисленных наблюдений датского астронома Т. Браге (1546–1601), изложил законы движения планет:

1. Планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.

2. Радиус-вектор планеты за равные промежутки времени описывает одинаковые площади.

3. Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит.

Из первого закона Кеплера следует, что траектория планеты – плоская кривая. С учетом этого обстоятельства из второго закона Кеплера следует, что сила, заставляющая планету двигаться по замкнутым орбитам, направлена к Солнцу. Определим, как эта сила меняется с изменением расстояния от Солнца и как она зависит от массы планеты. Предположим, что планета движется не по эллипсу, а по кругу, в центре которого находится Солнце. Ускорение планеты при равномерном движении по круговой орбите радиуса r выражается формулой .

Для планет, движущихся по круговым траекториям, третий закон Кеплера записывается в виде или , где 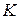– постоянная для всех планет Солнечной системы. Она называется постоянной Кеплера. Через параметры эллиптической орбиты постоянная Кеплера выражается формулой , где а – длина большой полуоси орбиты.

Сила, действующая на планету, будет равна , где m – масса планеты.

Мы доказали, что ускорения двух разных планет, обращающихся вокруг Солнца по круговым орбитам, обратно пропорциональны квадратам расстояний их от Солнца. Эта закономерность справедлива для всех планет, обращающихся вокруг Солнца.

Впоследствии И. Ньютон, изучая движение небесных тел, на основании законов Кеплера и основных законов динамики открыл всеобщий закон всемирного тяготения:между любыми двумя материальными точками действует сила взаимного притяжения, прямо пропорциональная произведению масс этих точек ( и ) и обратно пропорциональная квадрату расстояния между ними (r²):

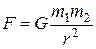(12.1)

Эта сила называется гравитационной(или силой всемирного тяготения).Силы тяготения всегда являются силами притяжения и направлены вдоль прямой, проходящей через взаимодействующие тела. Коэффициент пропорциональности G называется гравитационной постоянной.

Закон всемирного тяготения установлен для тел, принимаемых за материальные точки, т.е. для таких тел, размеры которых малы по сравнению с расстоянием между ними. Если же размеры взаимодействующих тел сравнимы с расстоянием между ними, то эти тела надо разбить на точечные элементы, подсчитать по формуле (12.1) силы притяжения между всеми попарно взятыми элементами, а затем геометрически их сложить (проинтегрировать), что является довольно сложной математической задачей.

Впервые экспериментальное доказательство закона всемирного тяготения для земных тел, а также числовое определение гравитационной постоянной G проведено английским физиком Г. Кавендишем (1731–1810). Принципиальная схема опыта Кавендиша, применившего крутильные весы,представлена на рис. 12.1.

Рис.12.1

Легкое коромысло А с двумя одинаковыми шариками массой m = 729 г подвешено на упругой нити В. На коромысле С укреплены на той же высоте массивные шары массой М = 158 кг. Поворачивая коромысло С вокруг вертикальной оси, можно изменять расстояние между шарами с массами т и М. Под действием пары сил, приложенных к шарам m со стороны шаров М, коромысло поворачивается в горизонтальной плоскости, закручивая нить до тех пор, пока момент сил упругости не уравновесит момента сил тяготения. Зная упругие свойства нити, по измеренному углу поворота можно найти возникающие силы притяжения, а так как массы шаров известны, то и вычислить значение G.

Значение G, приводимое в таблицах фундаментальных физических постоянных, принимается равным 6,6720·10^-11 Н·м²/кг², т.е. два точечных тела массой по 1 кг каждое, находящиеся на расстоянии 1 м друг от друга, притягиваются с силой 6,6720·10^-11 Н. Очень малая величина G показывает, что сила гравитационного взаимодействия может быть значительной только в случае больших масс. Так, сила тяготения между Землей и Луной имеет порядок 10²⁰ Н, а между двумя почти соприкасающимися молекулами кислорода – 10^-32 Н.

2. Гравитационная масса

Понятие массы было дано при изучении закона сохранения импульса (лекция 5, раздел 2). В основе этого понятия лежат инерционные свойства тел. Поэтому так определенную массу называют инертной массой и иногда обозначают посредством m⁽ⁱ⁾. Однако тела обладают не только свойствами инерции, но и способностью возбуждать в окружающем пространстве гравитационные поля. В этом отношении они аналогичны электрически заряженным телам, создающим вокруг себя электрическое поле. Инерция тел и их способность возбуждать в окружающем пространстве гравитационные поля не должны априори рассматриваться как взаимосвязанные и тем более тождественные свойства тел. Можно думать, что тела являются источниками гравитационных полей не потому, что они обладают инертными массами, а потому, что они несут особые заряды, аналогичные электрическим зарядам. Такие заряды называются гравитационными зарядами или гравитационными массами. Силы взаимодействия гравитационных масс, как показывает опыт, изменяются обратно пропорционально квадрату расстояния между ними. Для количественного определения гравитационных масс можно поступить так же, как поступают с электрическими зарядами в электростатике. Обозначим гравитационные массы взаимодействующих точечных тел посредством и . Тогда для силы их гравитационного притяжения можно написать

, (12.2)

где С – численный коэффициент, зависящий только от выбора единиц. Этому коэффициенту можно приписать произвольную размерность и произвольное численное значение. Тогда, считая единицы для r и F установленными, мы установим также единицу гравитационной массы и ее размерность, а формула (12.2) даст принципиальный способ измерения гравитационных масс.

Пропорциональность силы гравитационного взаимодействия тел их гравитационным массам не является физическим законом. Мы так вводим понятие гравитационной массы, что указанная пропорциональность соблюдается по определению. Физический закон, установленный Ньютоном, состоит в том, что сила гравитационного взаимодействия тел пропорциональна их инертным массам. Отсюда следует, что инертная масса тела пропорциональна его гравитационной массе. Единицы этих масс можно выбрать так, чтобы они были не только пропорциональны, но и численно равны между собой. Поэтому этот фундаментальный физический закон называется законом равенства, или эквивалентности инертной и гравитационной масс. Посмотрим, каковы его опытные основания и физические следствия.

Рассмотрим сначала свободное падение тел в поле тяжести Земли. По второму закону Ньютона m⁽ⁱ⁾ a =F, где F – сила тяжести. По смыслу под следует понимать инертную массу тела. Сила же тяжести может быть представлена в виде F= m^(g}g, где m^(g) – гравитационная масса того же тела. Заметим, что сейчас мы рассматриваем движение относительно инерциальной системы отсчета и поэтому не вводим никаких сил инерции. Все силы являются «реальными» в ньютоновском смысле. В частности, сила тяжести Fв нашем теперешнем рассмотрении есть сила только гравитационного притяжения между телом и Землей (центробежная сила в нее не входит). Второй закон Ньютона дает m^(i]a = m^(g]g, откуда

(12.3)

Так как инертная и гравитационная массы равны, то а = g. Все тела в поле тяжести Земли падают с одним и тем же ускорением. Этот экспериментальный факт, установленный впервые Галилеем, является подтверждением закона о равенстве инертной и гравитационной масс. Он справедлив и для любого гравитационного поля. В одном и том же гравитационном поле все тела при свободном падении приобретают одинаковое ускорение. Мы видим, что обобщенный закон Галилея по своему содержанию совершенно эквивалентен принципу равенства инертной и гравитационной масс.

Опыты Галилея имели малую точность. Значительно большей точности достигли Ньютон, а затем Бессель (1784–1846) в опытах с колебаниями маятника. В опытах Ньютона и Бесселя было установлено, что период колебаний математического маятника не зависит от материала, из которого он изготовлен. Это подтверждает закон равенства инертной и гравитационной масс. Относительная точность, с какой это равенство было установлено в опытах Бесселя, составляет 1/60 000.

Венгерский физик Этвеш (1848–1919) установил равенство инертной и гравитационной масс с относительной точностью 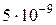. По сравнению с опытами Ньютона точность была повышена примерно в сто тысяч, а по сравнению с опытами Бесселя – более чем в десять тысяч раз. Идея опытов Этвеша заключается в следующем. Вес тела складывается из двух различных сил: силы гравитационного притяжения Земли и центробежной силы инерции. Первая сила пропорциональна гравитационной массе, вторая пропорциональна инертной массе m^(i]. Если бы инертная и гравитационная массы не были строго пропорциональны друг другу, то направление отвеса зависело бы от материала тела.

Одним из фундаментальных следствий теории относительности является связь между энергией и массой Е = mс². Здесь т означает инертную массу. Таким образом, всякая энергия обладает инертной массой. Закон эквивалентности инертной и гравитационной масс позволяет распространить это утверждение и на гравитационную массу. Всякая энергия должна обладать также и гравитационной массой. Высокая чувствительность опыта Этвеша позволила подвергнуть это заключение экспериментальной проверке. С этой целью Саузернс повторил опыт Этвеша с радиоактивными веществами. Опыт дал тот же результат: никакого различия между гравитационной и инертной массами обнаружено не было. Так как при радиоактивных превращениях энергия и инертная массы уменьшаются, то отсюда следует, что пропорционально уменьшается также и гравитационная масса. Таким образом, равенство инертной и гравитационной масс все время соблюдается.

Опыт Этвеша в усовершенствованном виде был повторен американским физиком Р.Дикке и его сотрудниками в 1961–1964 годах. Им удалось повысить точность результатов Этвеша более чем в 100 раз. Сравнивались грузы из меди и свинца, из золота и алюминия. С относительной точностью 3 • 10^-11 авторы констатировали равенство коэффициентов пропорциональности между гравитационной и инертной массами для этих материалов.

Опыт Дикке был повторен в усовершенствованном виде В.Б.Брагинским и В.И.Пановым в 1971 году. Равенство коэффициентов пропорциональности между гравитационной и инертной массами было подтверждено с относительной точностью 10^-12. Это то же самое, как если бы мы взвесили корабль водоизмещением в десять тысяч тонн вместе с грузом с точностью до одной сотой грамма.

Дорелятивистская физика не придавала существенного значения равенству инертной и гравитационной масс, рассматривая это равенство как случайное совпадение. Основополагающее значение закона эквивалентности инертной и гравитационной масс было понято Эйнштейном. Закон эквивалентности послужил для Эйнштейна отправным пунктом при построении общей теории относительности, называемой иначе релятивистской теорией гравитации. Этот закон является главным опытным фактом, на котором основана общая теория относительности. Последняя была бы неверна и от нее следовало бы отказаться, если бы было обнаружено малейшее нарушение закона эквивалентности инертной и гравитационной масс. Вот почему повышение и без того исключительной точности, с которой проверяется этот закон, имеет важное принципиальное значение, а не является просто спортивным увлечением с целью побития рекорда и установления нового.

3. Поле тяготения и его напряженность

Закон тяготения Ньютона определяет зависимость силы тяготения от масс взаимодействующих тел и расстояния между ними, но не показывает, как осуществляется это взаимодействие. Тяготение принадлежит к особой группе взаимодействий. Силы тяготения, например, не зависят от того, в какой среде взаимодействующие тела находятся. Тяготение существует и в вакууме.

Гравитационное взаимодействие между телами осуществляется с помощью поля тяготения,или гравитационного поля. Гравитационное поле – это особый вид материи, посредством которого осуществляется взаимное притяжение тел.Это поле порождается телами и является формой существования материи. Следовательно, это поле материально. Основное свойство поля тяготения заключается в том, что на всякое тело массой m, внесенное в это поле, действует сила тяготения, т.е.

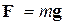(12.4)

Вектор g не зависит от m и называется напряженностью поля тяготения. Напряженность поля тяготенияопределяется силой, действующей со стороны поля на материальную точку единичной массы, и совпадает по направлению с действующей силой. Напряженность есть силовая характеристика поля тяготения.

Поле тяготения называется однородным,если его напряженность во всех точках одинакова, и центральным,если во всех точках поля векторы напряженности направлены вдоль прямых, которые пересекаются в одной точке, неподвижной по отношению к какой-либо инерциальной системе отсчета.

Для графического изображения силового поля используются силовые линии (линии напряженности). Силовые линии выбираются так, что вектор напряженности поля действует по касательной к силовой линии.

4. Работа в поле тяготения. Потенциал поля тяготения

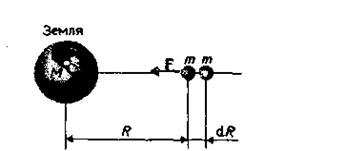
Рассмотрим, чему равна работа, совершаемая силами поля тяготения при перемещении в нем материальной точки массой т. Вычислим, например, какую надо затратить работу для удаления тела массой m от Земли. На расстоянии R (рис. 12.3) на данное тело действует сила .

Рис. 12.2

При перемещении этого тела на расстояние dR затрачивается работа

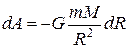(12.5)

Знак минус появляется потому, что сила и перемещение в данном случае противоположны по направлению (рис.12.2).

Если тело перемещать с расстояния R₁ до R₂, то затрачиваемая работа

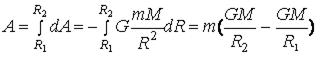(12.6)

Из формулы (12.6) вытекает, что затраченная работа в поле тяготения не зависит от траектории перемещения, а определяется лишь начальным и конечным положением тела, т.е. силы тяготения консервативны, а поле тяготения является потенциальным.

Известно, что работа, совершаемая консервативными силами, равна изменению потенциальной энергии системы, взятому со знаком минус, т.е.

Из формулы (12.6) получаем

(12.7)

Так как в формулы входят только разность потенциальных энергий в двух состояниях, то для удобства принимают потенциальную энергию при равной нулю. Тогда (12.7) запишется в виде . Так как первая точка была выбрана произвольно, то .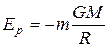

Величину 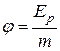называют потенциалом. Она является энергетической характеристикой поля тяготения. Потенциал поля тяготения 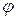–скалярная величина, определяемая потенциальной энергией тела единичной массы в данной точке поля или работой по перемещению единичной массы из данной точки поля в бесконечность. Таким образом, потенциал поля тяготения, создаваемого телом массой М, равен

(12.8)

где R – расстояние от этого тела до рассматриваемой точки.

Из формулы (12.8) вытекает, что геометрическое место точек с одинаковым потенциалом образует сферическую поверхность (R = const). Такие поверхности, для которых потенциал постоянен, называются эквипотенциальными.

Рассмотрим взаимосвязь между потенциалом поля тяготения ( 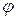) и его напряженностью (g). Из выражений (12.4) и (12.8) следует, что элементарная работа dА, совершаемая силами поля при малом перемещении тела массой т, равна .

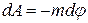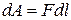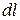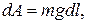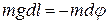С другой стороны, (d / – элементарное перемещение). Учитывая (12.3), получим, что т.е. или .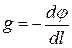

Величина 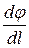характеризует изменение потенциала на единицу длины в направлении перемещения в поле тяготения.

Можно показать, что

(12.9)

где 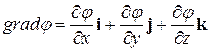– градиент скаляра 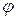. Знак минус в формуле (12.9) показывает, что вектор напряженности направлен в сторону убывания потенциала.

В качестве частного примера рассмотрим потенциальную энергию тела, находящегося на высоте h относительно Земли: 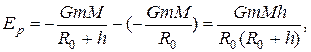где R₀ – радиус Земли.

Так как

и (12.10)

то, учитывая условие , получим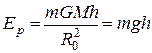

Таким образом, мы вывели формулу, которая постулировалась раньше. Разделив на 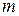, для потенциала гравитационного поля вблизи поверхности Земли получим формулу

(12.11)

5. Космические скорости

Для запуска ракет в космическое пространство надо в зависимости от поставленных целей сообщать им определенные начальные скорости, называемые космическими.

Первой космической(или круговой) скоростью называют такую минимальную скорость, которую надо сообщить телу, чтобы оно могло двигаться вокруг Земли по круговой орбите, т.е. превратиться в искусственный спутник Земли. На спутник, движущийся по круговой орбите радиусом R, действует сила тяготения Земли, сообщающая ему нормальное ускорение. По второму закону Ньютона .

Здесь 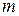– масса тела, М – масса Земли. Из написанного уравнения следует, что

(12.12)

Радиус Земли 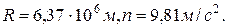Следовательно, .

Второй космической скоростьюназывают скорость 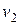, которую надо сообщить телу при запуске с Земли для того, чтобы оно вышло из сферы земного притяжения. Для нахождения 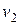воспользуемся законом сохранения энергии. При этом сопротивлением воздуха при прохождении тела через атмосферу Земли пренебрегаем. В момент запуска полная энергия равна

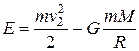(12.13)

При удалении тела на бесконечность полная энергия становится равной нулю. Поэтому, приравняв нулю выражении (12.13), получим для 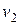значение