Потенциальная энергия упруго деформированного стержня равна 4 страница
и периодом
 (11.17)
(11.17)
Формула(11.17) справедлива для упругих колебаний в пределах, в которых выполняется закон Гука, т.е. когда масса пружины мала по сравнению с массой тела.
Потенциальная энергия пружинного маятника согласно (11.12) и (11.16) равна 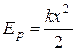 .
.
2. Физический маятник– это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси подвеса, не проходящей через центр масс С тела (рис. 11.4).
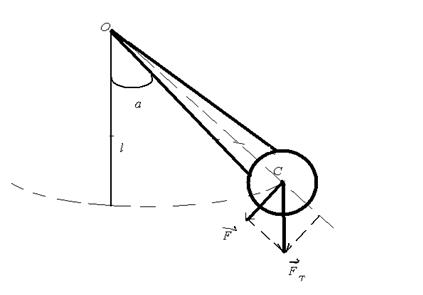
| Рис. 11.4 |
Пусть физический маятник совершает колебания вокруг неподвижной точки О. Обозначим массу маятника через m, длину маятника ОС, т.е. расстояние между точкой подвеса и центром масс маятника через 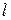 . Действуют две силы: сила тяжести
. Действуют две силы: сила тяжести 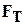 , приложенная к центру масс твердого тела С, и сила реакции опоры
, приложенная к центру масс твердого тела С, и сила реакции опоры 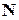 , приложенная к точке О.
, приложенная к точке О.
Если маятник отклонен из положения равновесия на некоторый угол а, то он под действием силы тяжести возвращается к положению равновесия, переходит его по инерции, отклоняется в противоположную сторону, затем опять переходит в положение равновесия и т.д. Центр тяжести маятника будет описывать дугу окружности. Возвращающая сила равна 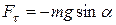 (знак минус обусловлен тем, что направления
(знак минус обусловлен тем, что направления 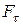 и
и 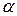 всегда противоположны). При малых отклонениях (
всегда противоположны). При малых отклонениях ( 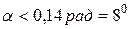 )
) 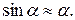
В соответствии с уравнением динамики вращательного движения твердого тела момент М возвращающей силы можно записать в виде
 (11.18)
(11.18)
где 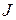 – момент инерции маятника относительно оси, проходящей через точку О.
– момент инерции маятника относительно оси, проходящей через точку О.
Таким образом, уравнение движения физического маятника можно записать в виде  или
или
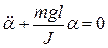 (11.19)
(11.19)
Обозначим 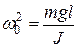 (11.20)
(11.20)
Получим уравнение
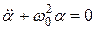 (11.21)
(11.21)
Оно идентично с (11.15). Следовательно, решение его известно:
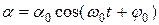 (11.22)
(11.22)
Из выражения (11.22) следует, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой 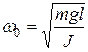 и периодом
и периодом
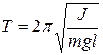 (11.23)
(11.23)
В этой формуле 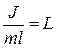 – приведенная длина физического маятника.
– приведенная длина физического маятника.
Точка О' на продолжении прямой ОС, отстоящая от оси подвеса на расстоянии приведенной длины L, называется центром качанийфизического маятника. Применяя теорему Штейнера, получим 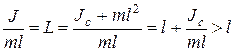 , т.е. 00' всегда больше ОС. Точка подвеса О и центр качаний О' обладают свойством взаимозаменяемости:если ось подвеса перенести в центр качаний, то точка О прежней оси подвеса станет новым центром качаний и период колебаний физического маятника не изменится.
, т.е. 00' всегда больше ОС. Точка подвеса О и центр качаний О' обладают свойством взаимозаменяемости:если ось подвеса перенести в центр качаний, то точка О прежней оси подвеса станет новым центром качаний и период колебаний физического маятника не изменится.
3. Математический маятник –это идеализированная система, состоящая из материальной точки массой т, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити.
Пусть длина маятника равна 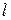 . Тогда момент инерции математического маятника есть
. Тогда момент инерции математического маятника есть
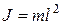 (11.24)
(11.24)
Так как математический маятник можно представить как частный случай физического маятника, предположив, что вся его масса сосредоточена в одной точке – центре масс, то, подставив выражение (11.24) в формулу (11.23), получим выражение для периода малых колебаний математического маятника
 (11.25)
(11.25)
Сравнивая формулы (11.23) и (11.25), видим, что если приведенная длина L физического маятника равна длине 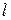 математического маятника, то их периоды колебаний одинаковы. Следовательно, приведенная длина физического маятника –это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.
математического маятника, то их периоды колебаний одинаковы. Следовательно, приведенная длина физического маятника –это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.
4. Сложение гармонических колебаний одного направления
и одинаковой частоты. Биения
Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, иными словами, колебания необходимо сложить. Рассмотрим гармонические колебания одного направления и одинаковой частоты
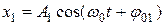 и
и 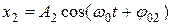 (11.26)
(11.26)
Очевидно, что уравнение результирующего колебания будет 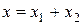 .
.
Подставим в него формулы (11.26), разложим их и введем обозначения
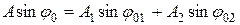 (11.27)
(11.27)
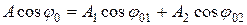 (11.28)
(11.28)
Здесь А и 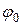 – амплитуда и начальная фаза суммарного колебания. При этих обозначениях уравнение результирующего колебания имеет вид
– амплитуда и начальная фаза суммарного колебания. При этих обозначениях уравнение результирующего колебания имеет вид
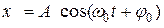 (11.29)
(11.29)
Из (11.29) видно, что результирующее колебание так же является гармоническим.
Для определения А и 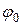 решается система, состоящая из уравнений (11.27) и (11.28). Решая их, получим
решается система, состоящая из уравнений (11.27) и (11.28). Решая их, получим
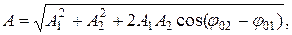 (11.30)
(11.30)
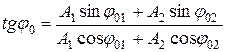 (11.31)
(11.31)
Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз  складываемых колебаний.
складываемых колебаний.
Проанализируем выражение (11.30) в зависимости от разности фаз  :
:
1) 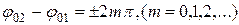 ,
,
тогда 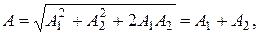 т.е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний;
т.е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний;
2)  ,
,
тогда 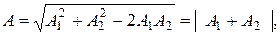 т.е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний.
т.е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний.
Для практики особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. В результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями.
Пусть амплитуды складываемых колебаний равны А, ачастоты равны 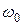 и
и 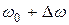 , причем
, причем 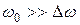 . Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:
. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю: 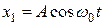 и
и 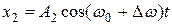
Складывая эти выражения и учитывая, что во втором сомножителе 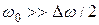 , найдем
, найдем
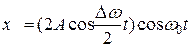 (11.32)
(11.32)
Получившееся выражение есть произведение двух колебаний. Так как 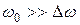 , то сомножитель, стоящий в скобках, почти не изменится, когда сомножитель
, то сомножитель, стоящий в скобках, почти не изменится, когда сомножитель 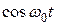 совершит несколько полных колебаний. Поэтому результирующее колебание х можно рассматривать как гармоническое с частотой
совершит несколько полных колебаний. Поэтому результирующее колебание х можно рассматривать как гармоническое с частотой 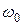 , а амплитудаизменится по следующему периодическому закону:
, а амплитудаизменится по следующему периодическому закону:
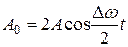 (11.33)
(11.33)
Частота изменения  в два раза больше частоты изменения косинуса (так как берется по модулю), т.е. частота биений равна разности частот складываемых колебаний:
в два раза больше частоты изменения косинуса (так как берется по модулю), т.е. частота биений равна разности частот складываемых колебаний: 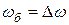 . Период биений
. Период биений 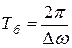 .
.
Определение частоты тона (звука определенной высоты) биений между эталонным и измеряемым колебаниями – наиболее широко применяемый на практике метод сравнения измеряемой величины с эталонной. Метод биений используется для настройки музыкальных инструментов, анализа слуха и т.д.
Любые сложные периодические колебания s = f(t) можно представить в виде суперпозиции одновременно совершающихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами, кратными циклической частоте
 (11.34)
(11.34)
Представление периодической функции в виде (11.34) связывают с понятием гармонического анализа сложного периодического колебания,или разложения Фурье.
Члены ряда Фурье, определяющие гармонические колебания с частотами 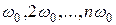 называются первой(или основной), второй, третьей и т.д. гармоникамисложного периодического колебания.
называются первой(или основной), второй, третьей и т.д. гармоникамисложного периодического колебания.
5. Сложение взаимно перпендикулярных колебаний
Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты 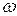 , происходящих во взаимно перпендикулярных направлениях вдоль осей х и у. Для простоты отсчета начальную фазу первого колебания возьмем равной нулю:
, происходящих во взаимно перпендикулярных направлениях вдоль осей х и у. Для простоты отсчета начальную фазу первого колебания возьмем равной нулю:
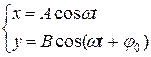 (11.35)
(11.35)
Разность фаз обоих колебаний равна 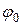 , A и В – амплитуды складываемых колебаний.
, A и В – амплитуды складываемых колебаний.
Уравнение траектории результирующего колебания находится исключением из выражений (11.35) параметра t. Запишем складываемые колебания в виде 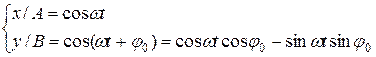
После несложных преобразований получим уравнение эллипса:
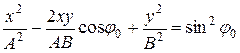 (11.36)
(11.36)
Оси эллипса ориентированы относительно координатных осей произвольно. Так как траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.
Ориентация осей эллипса и его размеры зависят от амплитуд складываемых колебаний и разности фаз. Рассмотрим некоторые частные случаи, представляющие физический интерес:
1) 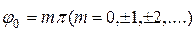 . В данном случае эллипс вырождается в отрезок прямой
. В данном случае эллипс вырождается в отрезок прямой
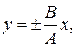 (11.37)
(11.37)
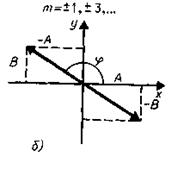
где знак плюс соответствует нулю и четным значениям т (рис. 11.5, а), знак минус – нечетным значениям т (рис. 11.5, б). Результирующее колебание является гармоническим колебанием с частотой 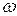 и амплитудой
и амплитудой 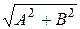 , совершающимся вдоль прямой (11.37), составляющей с осью х угол
, совершающимся вдоль прямой (11.37), составляющей с осью х угол 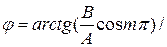
В данном случае имеем дело с линейно поляризованными колебаниями.
2) 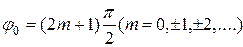 .Вданном случае уравнение примет вид
.Вданном случае уравнение примет вид
 (11.38)
(11.38)

| 
| 
|
| Рис.11.5, а | Рис.11.5, б | Рис.11.5, в |
Это уравнение эллипса, оси которого совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис.11.5, в). Кроме того, если А=В, то эллипс (11.38) вырождается в окружность. Такие колебания называются циркулярно поляризованными колебаниями или колебаниями, поляризованными по кругу.
Если частоты складываемых взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу.Форма этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. На рис. 11.6 представлены фигуры Лиссажу для различных соотношений частот (указаны слева) и разностей фаз (указаны вверху).
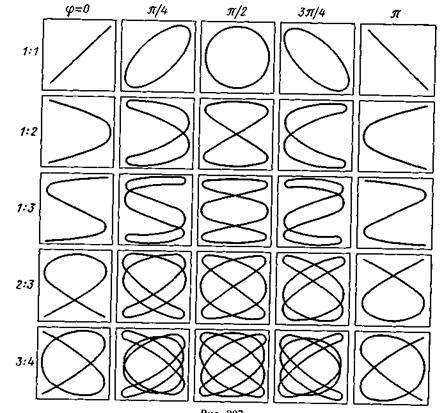
| Рис.11.6 |
Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, параллельными осям координат. По виду фигур можно определить неизвестную частоту по известной или определить отношение частот складываемых колебаний. Поэтому анализ фигур Лиссажу – широко используемый метод исследования соотношений частот и разности фаз складываемых колебаний, а также формы колебаний.
6. Свободные затухающие колебания
Рассмотрим свободные затухающие колебания– колебания, амплитуда которых из-за потерь энергии реальной колебательной системы с течением времени уменьшается. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических колебательных системах.
Закон затухающих колебаний определяется свойствами колебательных систем. Обычно рассматривают линейные системы– идеализированные реальные системы, в которых параметры, определяющие физические свойства системы, в ходе процесса не изменяются. Линейными системами являются, например, пружинный маятник при малых растяжениях пружины (когда справедлив закон Гука). Различные по своей природе линейные системы описываются идентичными линейными дифференциальными уравнениями, что позволяет подходить к изучению колебаний различной физической природы с единой точки зрения, а также проводить их моделирование, в том числе и на ЭВМ.
Дифференциальное уравнение свободных затухающих колебанийлинейной системы задается в виде
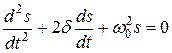 , (11.39)
, (11.39)
где s – колеблющаяся величина, описывающая тот или иной физический процесс,  = const – коэффициент затухания,
= const – коэффициент затухания, 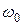 – циклическая частота свободных незатухающих колебаний той же колебательной системы, т.е. при
– циклическая частота свободных незатухающих колебаний той же колебательной системы, т.е. при 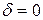 (при отсутствии потерь энергии) называется собственной частотойколебательной системы.
(при отсутствии потерь энергии) называется собственной частотойколебательной системы.
Решение уравнения (11.39) рассмотрим в виде
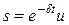 (11.40)
(11.40)
где u = u(t). После нахождения первой и второй производных выражения (11.40) и подстановки их в (11.39) получим
 (11.41)
(11.41)
Решение этого уравнения зависит от знака коэффициента перед искомой величиной. Рассмотрим случай, когда этот коэффициент положителен:
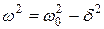 (11.42)
(11.42)
Тогда получим уравнение типа (11.4): 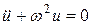 .
.
Решением его является функция 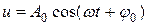 .
.
Таким образом, решение уравнения (11.39) в случае малых затуханий есть
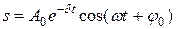 (11.43)
(11.43)
где 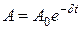 , (11.44)
, (11.44)
– амплитуда затухающих колебаний, 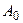 – начальная амплитуда.
– начальная амплитуда.
Промежуток времени 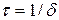 , в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации.
, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации.
Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Однако если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины. Тогда период затухающих колебаний равен 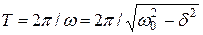
Если A(t) и A(t+T) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение 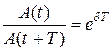 называется декрементом затухания,а его логарифм
называется декрементом затухания,а его логарифм
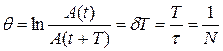 (11.45)
(11.45)
– логарифмическим декрементом затухания;N – число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания – постоянная для данной колебательной системы величина.
Для характеристики колебательной системы пользуются понятием добротностиQ, которая при малых значениях логарифмического декремента равна
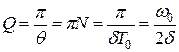 (11.46)
(11.46)
(так как затухание невелико ( 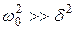 ), то Т принято считать равным T0).
), то Т принято считать равным T0).
Из формулы (11.46) следует, что добротность пропорциональна числу колебаний N, совершаемых системой за время релаксации.
Применим выводы, полученные для свободных затухающих колебаний линейных систем, для механических колебаний. В качестве примера рассмотрим пружинный маятник.
Для пружинного маятника массой т, совершающего малые колебания под действием упругой силы F=-kx, сила трения пропорциональна скорости, т.е. 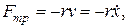 где
где 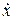 – коэффициент сопротивления;знак минус указывает на противоположные направления силы трения и скорости.
– коэффициент сопротивления;знак минус указывает на противоположные направления силы трения и скорости.
При данных условиях закон движения маятника будет иметь вид
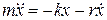 (11.47)
(11.47)
Используя формулу 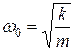 и принимая, что коэффициент затухания
и принимая, что коэффициент затухания
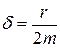 , (11.48)
, (11.48)
получим дифференциальное уравнение затухающих колебаний маятника: 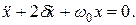
Из предыдущих выражений вытекает, что маятник колеблется по закону
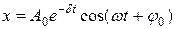 (11.49)
(11.49)
с частотой 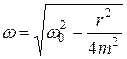 .
.
Добротность пружинного маятника 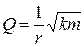 .
.
При увеличении коэффициента затухания  период затухающих колебаний растет и при
период затухающих колебаний растет и при 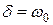 обращается в бесконечность, т.е. движение перестает быть периодическим. В данном случае колеблющаяся величина асимптотически приближается к нулю, когда
обращается в бесконечность, т.е. движение перестает быть периодическим. В данном случае колеблющаяся величина асимптотически приближается к нулю, когда 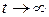 . Процесс не будет колебательным. Он называется апериодическим.
. Процесс не будет колебательным. Он называется апериодическим.
7. Вынужденные колебания
Чтобы в реальной механической колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью периодически действующей вынуждающей силы, изменяющейся по гармоническому закону:
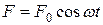 (11.50)
(11.50)
С учетом силы (11.50) закон движения для пружинного маятника запишется в виде 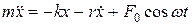 .
.
Используя соответствующие обозначения, придем к уравнению
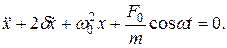 (11.51)
(11.51)
Дата добавления: 2015-08-08; просмотров: 971;
