Колебания, возникающие под действием внешней периодически изменяющейся силы, называются вынужденными механическими колебаниями. 2 страница

За скорость распространения этой негармонической волны (волнового пакета) принимают скорость перемещения максимума амплитуды волны, рассматривая тем самым максимум в качестве центра волнового пакета. При условии, что 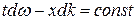, получим

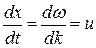(11.74)

Скорость и есть групповая скорость.Ее можно определить как скорость движения группы волн, образующих в каждый момент времени локализованный в пространстве волновой пакет. Хотя выражение (11.74) получено для волнового пакета из двух составляющих, можно доказать, что оно справедливо в самом общем случае. Рассмотрим связь между групповой и фазовой скоростями. Получим

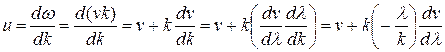(11.75)

Из формулы (11.75) вытекает, что и может быть как меньше, так и больше v в зависимости от знака .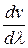

В недиспергирующей среде и групповая скорость совпадает с фазовой.

Понятие групповой скорости очень важно, так как именно она фигурирует при измерении дальности в радиолокации, в системах управления космическими объектами и т.д. В теории относительности доказывается, что групповая скорость 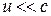, в то время как для фазовой скорости ограничений не существует.

13. Энергия упругой волны

Пусть в некоторой среде распространяется в направлении оси х плоская продольная волна x = a cos ( wt − kx).

Выделим в среде элементарный объем ДV, настолько малый, что скорость движения и деформацию во всех точках этого объема можно было считать одинаковыми и равными, соответственно, 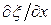и .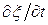

Обозначим плотность среды через 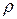, а скорость движения – через 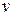. Тогда масса 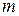выделенного объема равна 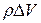. Выделенный нами объем обладает кинетической энергией

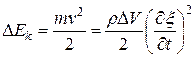(11.76)

Относительное удлинение цилиндра есть 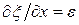. Модуль Юнга среды – Е. Тогда рассматриваемый объем обладает также потенциальной энергией упругой деформации

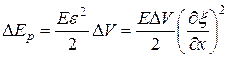(11.77)

Так как скорость распространения продольных волн 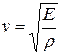, заменим в (11.77) модуль Юнга через сх². Тогда выражение для потенциальной энергии объема ДV примет вид

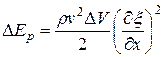(11.78)

Выражения (11.76) и (11.78) в сумме дают полную энергию

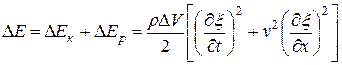(11.79)

Разделив эту энергию на объем ДV, в котором она содержится, получим плотность энергии

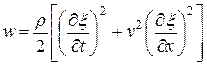(11.80)

Дифференцируем выражение для 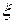один раз по t, другой раз по x . Получим , .

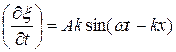Подставив эти выражения в формулу (11.80) и приняв во внимание, что k²х² = щ², получим

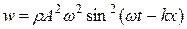(11.81)

В поперечной волне плотность энергии получает такое же выражение.

Из (11.81) следует, что плотность энергии в каждый момент времени в разных точках пространства различна. В одной и той же точке плотность энергии изменяется со временем по закону квадрата синуса. Среднее значение квадрата синуса равно 1/2. Соответственно, среднее по времени значение плотности энергии в каждой точке среды равно

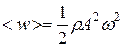(11.82)

Плотность энергии и ее среднее значение пропорциональны плотности среды с, квадрату частоты щ и квадрату амплитуды волны А. Подобная зависимость имеет место не только для незатухающей плоскости волны, но и для других видов волн (плоской затухающей, сферической и т.д.).

Итак, среда, в которой распространяется волна, обладает дополнительным запасом энергии. Эта энергия доставляется от источника колебаний в различные точки среды самой волной; следовательно, волна переносит с собой энергию. Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии через эту поверхность. Если через данную поверхность переносится за время dt энергия dЕ, то поток энергии Ф равен

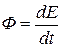(11.83)

Поток энергии – скалярная величина, размерность которой равна размерности энергии, деленной на размерность времени, т.е. совпадает с размерностью мощности. В соответствии с этим Ф измеряется в ваттах, эрг/с и т. п.

Поток энергии в разных точках среды может быть различной интенсивности. Для характеристики течения энергии в разных точках пространства вводится векторная величина, называемая плотностью потока энергии. Эта величина численно равна потоку энергии через единичную площадку, помещенную в данной точке перпендикулярно направлению, в котором переносится энергия. Направление вектора плотности потока энергии совпадает с направлением переноса энергии.

Пусть через площадку 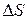, перпендикулярную направлению распространения волны, переносится за время ∆t энергия ∆Е. Тогда плотность потока энергии равна

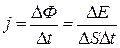(11.84)

Через площадку 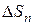(рис. 6.1) за время ∆t будет перенесена энергия ∆Е, заключенная в объеме цилиндра с основанием 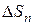и высотой v∆t (v – фазовая скорость волны). Если размеры цилиндра достаточно малы (за счет малости 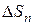и ∆t) для того, чтобы плотность энергии во всех точках цилиндра можно было считать одинаковой, то ∆Е можно найти как произведение плотности энергии w на объем цилиндра, равный : .

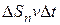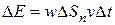Подставив это выражение в формулу (11.84), получим выражение для плотности потока энергии:

(11.85)

Наконец, введя вектор v, модуль которого равен фазовой скорости волны, а направление совпадает с направлением распространения волны (и переноса энергии), можно написать, что

j = wv(11.86)

Рис. 11.14

Мы получили выражение для вектора плотности потока энергии (интенсивности волны). Этот вектор был впервые введен на рассмотрение выдающимся русским физиком Н.А.Умовым и называется вектором Умова. Вектор (6.10), как и плотность энергии w, различен в разных точках пространства, а в данной точке изменяется со временем по закону квадрата синуса. Его среднее значение равно .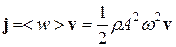

Данное выражение, так же как и (11.82), справедливо для волны любого вида (сферической, затухающей и т.д.).

14. Интерференция волн

Согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов связывают с понятием когерентности. Волныназываются когерентными, если они имеют постоянную разность фаз. На рис.11.15 показана картина интерференции, наблюдаемая в случае, когда в воду бросают два камня.

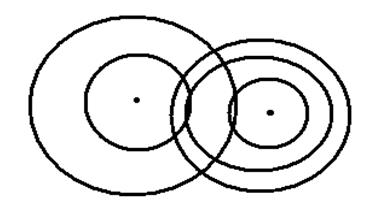
Рис.11.15

Рассмотрим интерференцию двух волн одинаковой амплитуды, исходящих из когерентных источников и 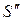и встречающихся в точке Р (рис.11.16).

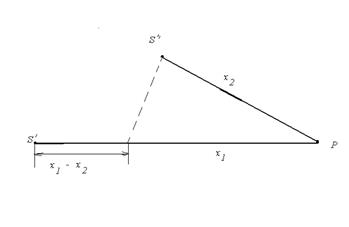
Рис.11.16

Согласно уравнению волны, смещения, вызванные в точке Р первой и второй волнами, равны соответственно и .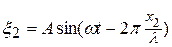

Тогда результат сложения определится разностью фаз .

Если 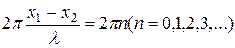, то в точке Р будет максимум: колебания максимально усилят друг друга и результирующая амплитуда будет равна 2А.

Если же , то в точке Р будет минимум: колебания взаимно погасятся и результирующая амплитуда будет равна нулю.

Условия максимума и минимума можно записать еще и так:

(11.87)

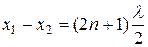(11.88)

Разность 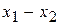называется разностью хода волн или разностью хода лучей.

Следовательно, в точке Р будет максимум, если разность хода волн составляет четное число полуволн; если разность хода волн составляет нечетное число полуволн, то в точке Р будет минимум.

Так как волны распространяются по всем направлениям, то в пространстве наблюдаем чередование областей усиления и уменьшения колебаний. Это явление и представляет собой интерференционную картину.

15. Стоячие волны

Особым случаем интерференции являются стоячие волны– это волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами. Для вывода уравнения стоячей волны предположим, что две плоские волны распространяются навстречу друг другу вдоль оси х в среде без затухания, причем обе волны характеризуются одинаковыми амплитудами и частотами. Кроме того, начало координат выберем в точке, в которой обе волны имеют одинаковую фазу, а отсчет времени начнем с момента, когда фазы обеих волн равны нулю. Тогда уравнения волны, распространяющейся вдоль положительного направления оси х, и волны, распространяющейся ей навстречу, соответственно будут иметь вид

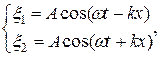(11.89)

Сложив эти уравнения, получим уравнение стоячей волны:

(11.90)

Из уравнения стоячей волны (11.90) вытекает, что в каждой точке этой волны происходят колебания той же частоты 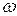с амплитудой 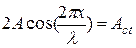, зависящей от координаты х рассматриваемой точки.

В точках среды, где

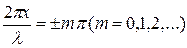(11.91)

амплитуда колебаний достигает максимального значения, равного 2 А. В точках среды, где

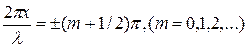(11.92)

амплитуда колебаний обращается в нуль. Точки, в которых амплитуда колебаний максимальна, называются пучностями стоячей волны,а точки, в которых амплитуда колебаний равна нулю, называются узлами стоячей волны.Точки среды, находящиеся в узлах, колебаний не совершают.

Из выражений (11.91) и (11.92) можно получить соответственно координаты пучностей и узлов:

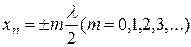(11.93)

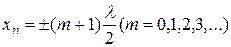(11.94)

Можно показать, что расстояния между двумя соседними пучностями и двумя соседними узлами одинаковы и равны 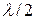. Расстояние между соседними пучностью и узлом стоячей волны равно .

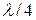В отличие от бегущей волны, все точки которой совершают колебания с одинаковой амплитудой, но с запаздыванием по фазе (в уравнении (11.89) бегущей волны фаза колебаний зависит от координаты х рассматриваемой точки), все точки стоячей волны между двумя узлами колеблются с разными амплитудами, но с одинаковыми фазами (в уравнении (11.90) стоячей волны аргумент косинуса не зависит от х). При переходе через узел множитель 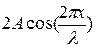меняет свой знак, поэтому фаза колебаний по разные стороны от узла отличается на 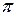, т.е. точки, лежащие по разные стороны от узла, колеблются в противофазе.

Образование стоячих волн наблюдают при интерференции бегущей и отраженной волн. Например, если конец веревки закрепить неподвижно, то отраженная в месте закрепления веревки волна будет интерферировать с бегущей волной и образует стоячую волну. На границе, где происходит отражение волны, в данном случае получается узел. Будет ли на границе отражения узел или пучность, зависит от соотношения плотностей сред. Если среда, от которой происходит отражение, менее плотная, то в месте отражения получается пучность (рис. 11.17, а), если более плотная – узел (рис. 11.17, б). Образование узла связано с тем, что волна, отражаясь от более плотной среды, меняет фазу на противоположную и у границы происходит сложение колебаний противоположных направлений, в результате чего получается узел. Если же волна отражается от менее плотной среды, то изменения фазы не происходит и у границы колебания складываются с одинаковыми фазами – получается пучность.

Если рассматривать бегущую волну, то в направлении ее распространения переносится энергия колебательного движения. В случае же стоячей волны переноса энергии нет, так какпадающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях. Поэтому полная энергия результирующей стоячей волны, заключенной между узловыми точками, остается постоянной. Лишь в пределах расстояний, равных половине длины волны, происходят взаимные превращения кинетической энергии в потенциальную и обратно.

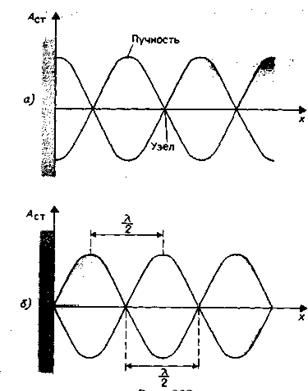
Рис.11.17

16. Характеристика звуковых волн

Звуковыми(или акустическими) волнами называются распространяющиеся в среде упругие волны, обладающие частотами в пределах 16-20000Гц. Волны указанных частот, воздействуя на слуховой аппарат человека, вызывают ощущение звука. Волны с 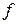< 16 Гц (инфразвуковые)и 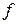>>20 кГц (ультразвуковые)органами слуха человека не воспринимаются.

Звуковые волны в газах и жидкостях могут быть только продольными, так как эти среды обладают упругостью лишь по отношению к деформациям сжатия (растяжения). В твердых телах звуковые волны могут быть как продольными, так и поперечными, так как твердые тела обладают упругостью по отношению к деформациям сжатия (растяжения) и сдвига.

Интенсивностью звука(или силой звука)называется величина, определяемая средней по времени энергией, переносимой звуковой волной в единицу времени сквозь единичную площадку, перпендикулярную направлению распространения волны: I=W/(St).

Единица интенсивности звука в СИ – ватт на метр в квадрате(Вт/м²).

Чувствительность человеческого уха различна для разных частот. Для того чтобы вызвать звуковое ощущение, волна должна обладать некоторой минимальной интенсивностью, но если эта интенсивность превышает определенный предел, то звук не слышен и вызывает только болевое ощущение. Таким образом, для каждой частоты колебаний существует наименьшая (порог слышимости)и наибольшая (порог болевого ощущения)интенсивность звука, которая способна вызвать звуковое восприятие. На рис. 11.18 представлена зависимость порогов слышимости и болевого ощущения от частоты звука. Область, расположенная между этими двумя кривыми, является областью слышимости.

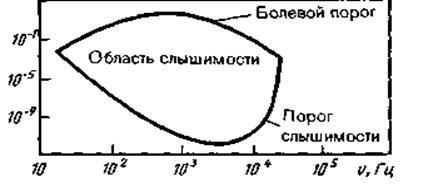
Рис.11.18

Если интенсивность звука является величиной, объективно характеризующей волновой процесс, то субъективной характеристикой звука, связанной с его интенсивностью, является громкость звука,зависящая от частоты. По физиологическому закону Вебера-Фехнера, с ростом интенсивности звука громкость возрастает по логарифмическому закону. На этом основании вводят объективную оценку громкости звука по измеренному значению его интенсивности: 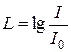, где – интенсивность звука на пороге слышимости, принимаемая для всех звуков равной 10 ¹² Вт/м². Величина L называется уровнем интенсивности звука и выражается в белах(в честь изобретателя телефона Белла). Обычно пользуются единицами, в 10 раз меньшими,– децибелами(дБ).

Физиологической характеристикой звука является уровень громкости,который выражается в фонах(фон). Громкость для звука в 1000 Гц (частота стандартного чистого тона) равна 1 фон, если его уровень интенсивности равен 1 дБ. Например, шум в вагоне метро при большой скорости соответствует ≈90 фон, а шепот на расстоянии 1 м – ≈ 20 фон.

Реальный звук является наложением гармонических колебаний с большим набором частот, т.е. звук обладает акустическим спектром,который может быть сплошным(в некотором интервале присутствуют колебания всех частот) и линейчатым(присутствуют отделенные друг от друга определенные частоты).

Помимо громкости звуковое ощущение характеризуется еще высотой и тембром. Высота звука– качество звука, определяемое человеком субъективно на слух и зависящее от частоты звука. С ростом частоты увеличивается и высота звука, т.е. звук становится «выше». Характер акустического спектра и распределения энергии между определенными частотами определяет своеобразие звукового ощущения, называемое тембром звука.Так, различные певцы, берущие одну и ту же ноту, имеют различный акустический спектр, т.е. они имеют различный тембр.

Источником звука может быть всякое тело, колеблющееся в упругой среде со звуковой частотой (например, в струнных инструментах источником звука является струна, соединенная с корпусом инструмента).

Совершая колебания, тело вызывает колебания прилегающих к нему частиц среды с такой же частотой. Состояние колебательного движения последовательно передается к все более удаленным от тела частицам среды, т.е. в среде распространяется волна с частотой колебаний, равной частоте ее источника, и с определенной скоростью, зависящей от плотности и упругих свойств среды.

Скорость звука в газе не зависит от давления р газа, но возрастает с повышением температуры. Чем больше молярная масса газа, тем меньше в нем скорость звука. Например, при Т = 273 К скорость звука в воздухе

(М = 29∙10 ^-3 кг/моль) 331 м/с, в водороде (М – 2∙10 ^-3 кг/моль) v = 1260 м/с.

При распространении звука в атмосфере необходимо учитывать целый ряд факторов: скорость и направление ветра, влажность воздуха, молекулярную структуру газовой среды, явление преломления и отражения звука на границе двух сред. Кроме того, любая реальная среда обладает вязкостью, поэтому наблюдается затухание звука, т.е. уменьшение его амплитуды и, следовательно, интенсивности звуковой волны по мере ее распространения. Затухание звука обусловлено в значительной мере его поглощением в среде, связанным с необратимым переходом звуковой энергии в другие формы энергии (в основном в тепловую).

Для акустики помещений большое значение имеет реверберация звука– процесс постепенного затухания звука в закрытых помещениях после выключения его источника. Если помещения пустые, то происходит медленное затухание звука и создается «гулкость» помещения. Если звуки затухают быстро (при применении звукопоглощающих материалов), то они воспринимаются приглушенными. Время реверберации– это время, в течение которого интенсивность звука в помещении ослабляется в миллион раз, а его уровень – на 60 дБ. Помещение обладает хорошей акустикой, если время реверберации составляет 0,5–1,5с.

17. Эффект Доплера в акустике

Эффектом Доплера(австрийский физик, математик и астроном (1803–1853)) называется изменение частоты колебаний, воспринимаемой приёмником при движении источника этих колебаний и приёмника относительно друг друга. Например, из опыта известно, что тон гудка поезда повышается по мере его приближения к платформе и понижается при удалении, т.е. движение источника колебаний (гудка) относительно приемника (уха) изменяет частоту принимаемых колебаний.

Для рассмотрения эффекта Доплера предположим, что источник и приемник звука движутся вдоль соединяющей их прямо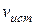й; и 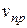– соответственно скорости движения источника и приемника, причем они положительны, если источник (приемник) приближается к приемнику (источнику), и отрицательны, если удаляется. Частота колебаний источника равна .

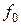1. Источник и приемник покоятся относительно среды,т.е. 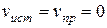. Если v – скорость распространения звуковой волны в рассматриваемой среде, то длина волны 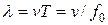. Распространяясь в среде, волна достигнет приемника и вызовет колебания его звукочувствительного элемента с частотой .

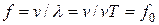Следовательно, частота 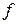звука, которую зарегистрирует приемник, равна частоте 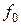, с которой звуковая волна излучается источником.

2. Приемник приближается к источнику, а источник покоится,т.е. 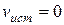, 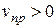. В данном случае скорость распространения волны относительно приемника станет равной 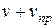.Так как длина волны при этом не меняется, то 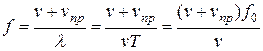, т.е. частота колебаний, воспринимаемых приемником, в 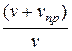раз больше частоты колебаний источника.

3. Источник приближается к приемнику, а приемник покоится,т.е. , 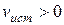. Скорость распространения колебаний зависит лишь от свойств среды, поэтому за время, равное периоду колебаний источника, излученная им волна пройдет в направлении к приемнику расстояние vT (равное длине волны 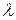) независимо от того, движется ли источник или покоится. За это же время источник пройдет в направлении волны расстояние 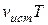, т.е. длина волны в направлении движения сократится и станет равной 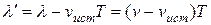. Тогда 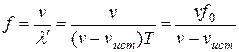т.е. частота v колебаний, воспринимаемых приемником, увеличится в 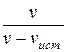раз. В случаях 2 и 3, если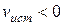 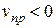, знак будет обратным.

4. Источник и приемник движутся относительно друг друга.Используя результаты, полученные для случаев 2 и 3, можно записать выражение для частоты колебаний, воспринимаемых источником:

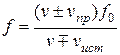(11.95)

причем верхний знак берется, если при движении источника или приемника происходит их сближение, нижний знак – в случае их взаимного удаления.

Из приведенных формул следует, что эффект Доплера различен в зависимости от того, движется ли источник или приемник. Если направления скоросте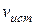й и 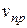не совпадают с проходящей через источник и приемник прямой, то вместо этих скоростей в формуле (11.95) надо брать их проекции на направление этой прямой.

18. Ультразвук и eго применение

По своей природе ультразвук представляет собой упругие волны, и в этом он не отличается от звука. Однако ультразвук, обладая высокими частотами (>20кГц) и, следовательно, малыми длинами волн, характеризуется особыми свойствами, что позволяет выделить его в отдельный класс явлений. Из-за малых длин ультразвуковые волны, как и свет, могут быть получены в виде строго направленных пучков.

Ультразвуки широко используются в технике, например, для направленной подводной сигнализации, обнаружения подводных предметов и определения глубин (гидролокатор, эхолот). Так, в эхолоте от пьезокварцевого генератора, укрепленного на судне, посылаются направленные ультразвуковые сигналы, которые, достигнув дна, отражаются от него и возвращаются обратно. Зная скорость их распространения в воде и определяя время прохождения (от подачи до возвращения) ультразвукового сигнала, можно вычислить глубину. Прием эха также производится с помощью пьезокварца. Звуковые колебания, дойдя до пьезокварца, вызывают в нем упругие колебания, в результате чего на противоположных поверхностях кварца возникают электрические заряды, которые измеряются.

Если пропускать ультразвуковой сигнал через исследуемую деталь, то можно обнаружить в ней дефекты по характерному рассеянию пучка и по появлению ультразвуковой тени. На этом принципе создана целая отрасль техники – ультразвуковая дефектоскопия,начало которой положено С.Я.Соколовым (1897–1957). Применение ультразвука легло также в основу новой области акустики – акустоэлектроники,позволяющей на ее основе разрабатывать приборы для обработки сигнальной информации в микрорадиоэлектронике.