Особенности динамики систем с наблюдателями

Запишем полную систему уравнений, описывающую объект управления с регулятором и наблюдателем:

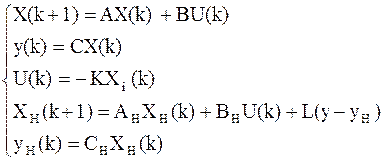
Предполагаем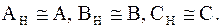

Введем новую переменную:

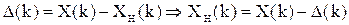
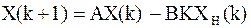
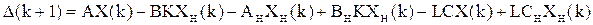
Перепишем исходную систему уравнений, используя новую переменную:

.

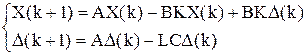Приведем подобные в последнем выражении:

.

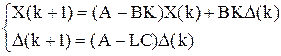Перепишем это выражение в матричном виде:

.

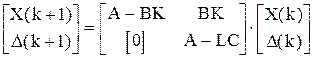Матрица правой части получилась треугольная. Запишем характеристическое уравнение полученной системы:

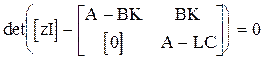
Известно, что определитель для треугольной квадратной матрицы имеет следующий вид:

det(zI-A+BK)×det(zI-A+LC)=0,

т.е. собственные числа этой матрицы представляют собой две группы, первая из которых - это группа желаемых корней синтезируемой системы, вторая группа корней - это группа желаемых корней наблюдателя, используемого для оценки вектора состояния объекта.

Динамика полной системы с наблюдателем и регулятором описывается двумя независимыми наборами корней:

желаемые корни системы реализуются с помощью матрицы K;

желаемый набор корней наблюдателя состояния реализуется с помощью матрицы обратных связей L.

Оба набора корней формируются независимо друг от друга, следовательно, динамические свойства фильтра и объекта взаимно друг на друга не влияют, но процессы по выходу объекта, до тех пор пока не закончатся переходные процессы в наблюдателе, зависят от последних.

Наблюдатель - неуправляемая подсистема.