Расчет корректора
Введем новую переменную:
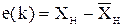
и для неё запишем разностное уравнение, воспользовавшись уравнениями объекта и наблюдателя:
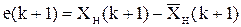 .
.
После преобразований получаем следующее выражение:
 ,
,
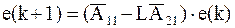 ;
;
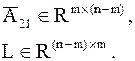 .
.
Последнее уравнение даёт возможность записать характеристическое уравнение наблюдателя пониженного порядка, а оно, в свою очередь, найти параметры корректора наблюдателя (матрицы L), при заданных требованиях к динамическим свойствам наблюдателя, заданных корнями:
 .
.
Достоинства наблюдателя, рассчитанного таким способом:
· порядок наблюдателя (n-m), значит переходные процессы в нем будут длиться не более (n-m) шагов, в случае реализации в нем процессов минимальной длительности.
Недостатки:
· так как в структуре наблюдателя полностью присутствуют матрицы A, B, L вычислительных ресурсов при своём функционировании он требует не меньше, чем обычный наблюдатель.
Оценка вектора состояния в новом базисе имеет вид:
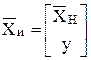 ; оценка вектора состояния в старом базисе тогда
; оценка вектора состояния в старом базисе тогда 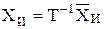 .
.
В этом случае управление вычисляется по следующей процедуре:
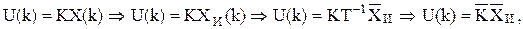
где 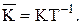
Дата добавления: 2015-08-04; просмотров: 776;
