Синтез одноканальных астатических систем с использованием матричной процедуры

Модель объекта:

.

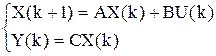Рис. 3.6

Рассмотрим процедуру синтеза на примере объекта третьего порядка:

;

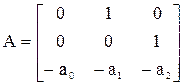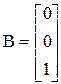
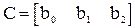
Расширим модель объекта, добавив разностное уравнение интегратора:

.

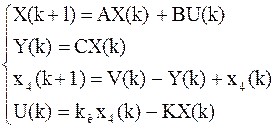Полная система уравнений объекта с регулятором приведена ниже:

.

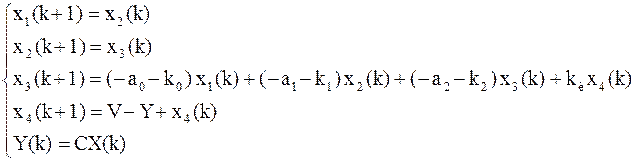Матрица 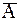полной системы выглядит следующим образом:

.

Приравняв характеристический полином всей системы желаемому характеристическому полиному, составленному из желаемых корней, а далее приравняв коэффициенты этих полиномов при равных степенях оператора z, получаем систему уравнений для нахождения параметров регулятора, она приведена ниже в матричной форме. Матрицы хорошо структурированы и методом математической индукции полученный результат может быть распространен на системы любого порядка.

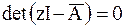
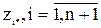
На примере системы третьего порядка видно, что система уравнений для поиска параметров регулятора хорошо структурирована. Для любого порядка методом математической индукции можно записать матрицу левой части и вектор правой части этого уравнения.

Ограничение операторной процедуры модального метода синтеза:

операторную процедуру можно применять для объектов, у которых корни числителя (нули) лежат в круге единичного радиуса. Для матричной процедуры модального метода синтеза такого ограничения нет.

Для реализации матричной процедуры модального метода синтеза необходимо иметь полную информацию о векторе состояния, либо иметь оценку вектора состояния.