Упругая волна в идеальном газе

Будем для определенности рассматривать распространение звуковой волны в воздухе (вдоль оси x).

Как и прежде, выделим элемент сечением S и длиной Δx (рис. 2.2).

На основания x и x + Δx этого элемента со стороны окружающего воздуха будут действовать силы F(x) и F(x + Δx). Их принято задавать давлением в этих сечениях:

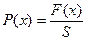и .

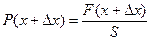В отсутствии волны давление в обоих сечениях одинаково — Р.

При прохождении волны выделенный элемент смещается и деформируется, а давление газа меняется и становится функцией и координаты (х) и времени (t).

Рис. 2.2

Вновь запишем знакомое уравнение динамики для рассматриваемого элемента газа:

F = m · a.

В нашем случае:

m = ρ sΔx

,

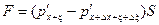
Здесь 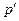— новое давление газа, возникающее при прохождении волны.

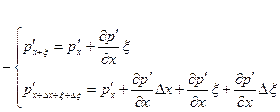
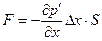
Определив таким образом силу, действующую на выделенный элемент газа, вернёмся к уравнению Ньютона:

или

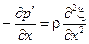(2.5)

Постараемся теперь выяснить, как меняется давление 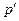вдоль оси x ( ).

Акустическая волна в газе — «быстротекущий» процесс. «Быстротекущий» по сравнению с процессом теплопроводности, поэтому термодинамически волны принято описывать адиабатическим процессом 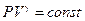. Здесь γ — постоянная адиабаты. Для воздуха, например, γ = 1.4.

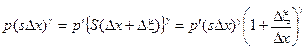
Понятно, что 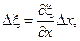поэтому

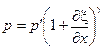
Скобку разложим в биномиальный ряд, ограничившись его первыми членами.

[Биноминальный ряд: ].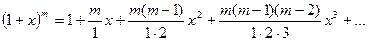

.

Отсюда следует:

.

.

.

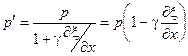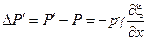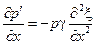Этот результат мы и используем в уравнении движения (2.5):

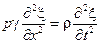
Осталось слегка преобразовать этот результат:

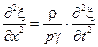
и сравнить его с уравнением (2.1).

Выводы:

1. Мы вновь получили дифференциальное волновое уравнение.

2. Скорость распространения акустической волны в газе зависит только от его состояния

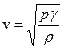. (2,6)

.

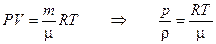
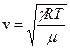3. Скорость звука в воздухе при нормальных условиях ( 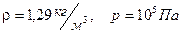) равна:

.

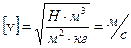Теперь понятно, почему во всём мире воздушные лайнеры летают со скоростью 900 км/час. Они вплотную подобрались к скорости звука. Летать с большой скоростью - значит преодолеть «звуковой барьер». Для этого нужны совсем другие самолёты. И другие деньги.