Энергетические характеристики упругих волн. Вектор Умова

Вновь возбудим продольную волну в стержне.

Выделим элемент стержня Δx. Элемент возьмём настолько малым, чтобы можно было считать скорость и деформацию разных участков элемента одинаковыми.

Покажем, что при прохождении волны выделенный элемент приобретает как кинетическую, так и потенциальную энергию.

1. Кинетическая энергия

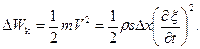
Здесь 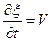— скорость элемента стержня (но не волны!).

Плотность кинетической энергии

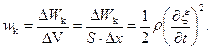(2.7)

2. Потенциальная энергия.

Эта энергия определяется работой упругих сил 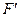, возникающих в стержне при его деформации. Деформация непременно сопровождает волновой процесс в стержне.

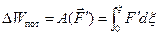(2.8)

Здесь: упругая сила ,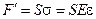

ξ — деформация участка Δx:

,

.

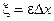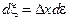Все эти сведения соберём в уравнение (2.8):

.

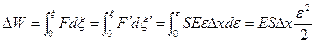Плотность потенциальной энергии:

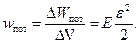
Плотность энергии в бегущей упругой волне складывается из плотностей кинетической и потенциальной энергий:

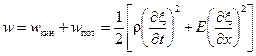. (2.9)

Обратимся теперь к частному, но очень важному случаю: пусть в стержне протекает бесконечный гармонический волновой процесс.

Уравнение плоской волны

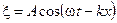. (2.10)

Скорость частиц стержня, обусловленная волной:

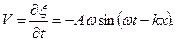. (2.11)

Относительная деформация:

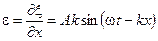. (2.12)

Сравнивая (2.11) и (2.12) с уравнением (2.10), приходим к интересным выводам:

1. В моменты максимального смещения (ξ) скорость частиц (V) и относительная деформация (ε) равны нулю.

2. Скорость и деформация достигают максимальных значений в тех точках, где смещение равно нулю (ξ = 0).

Отсюда следует, что плотности кинетической и потенциальной энергий меняются синфазно. В любом сечении стержня они одновременно достигают максимума и также одновременно исчезают:

.

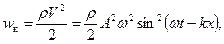
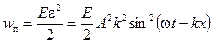Плотность полной энергии:

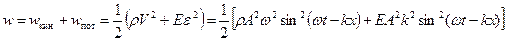
Вспомним, что волновое число 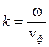, а фазовая скорость продольной волны в твёрдом теле (2.4)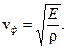

Теперь плотность энергии можно представить в виде:

.

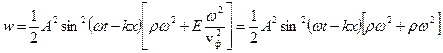Полученный результат означает, что плотность кинетической и потенциальной энергий не только колеблются синфазно, но и в заданном сечении они в любой момент времени равны друг другу:

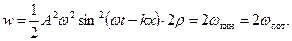(2.13)

.

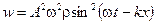Плотность энергии меняется вдоль оси стержня согласно закону .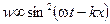

Среднее значение объёмной плотности энергии можно получить, усреднив квадрат синуса :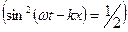

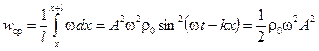. (2.14)

Энергия вдоль стержня перемещается вместе с волной с фазовой скоростью .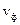

Вместе с волной ежесекундно через поперечное сечение стержня единичной площади переносится энергия

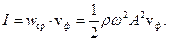(2.15)

Эта величина является основной энергетической характеристикой волны. Она получила название интенсивность.

Интенсивность равна количеству энергии, которая переносится волной за единицу времени через единичную площадку, ориентированную перпендикулярно направлению распространения волны.

Важно, конечно, отметить, что интенсивность волны пропорциональна квадрату амплитуды смещения (А²) и квадрату частоты колебаний (ω²).

Более универсальной характеристикой энергии волны является вектор плотности потока энергии (вектор Умова).

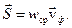(2.16)

Модуль этого вектора равен интенсивности волны, а по направлению вектор Умова совпадает с направлением распространения волны( ).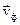

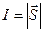
Понятие вектора плотности потока энергии ввёл русский физик-теоретик профессор Московского университета Николай Александрович Умов. В своё время профессор Умов ушёл в отставку в знак протеста против притеснения студентов правительством. Случилось это, правда, давно - в самом начале прошлого века.