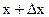Скорость звука в средах

1.1. Продольные волны в твёрдом теле

Нанесём удар по оси металлического (для определённости) стержня. В стержне возникает упругая волна деформации ξ = ξ(x).

Выделенный элемент стержня (Δx) не только сместится при прохождении волны, но и деформируется (рис.2.1). Это и понятно: ведь смещения разных сечений стержня будут разными. Например, если

ξ — смещение сечения x, а (ξ + Δξ) — смещение сечения (x + Δx), то

Δξ — абсолютная деформация выделенного элемента(Δx).

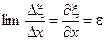— относительная деформация в сечении x.

По поводу этой характеристики сделаем два замечания.

Во-первых, это не усреднённое значение относительной деформации по всему элементу Δx, а локальная характеристика «в сечении».

Во-вторых, мы здесь воспользовались частной производной по координате, памятуя о том, что деформация при прохождении по стержню волны меняется ещё и во времени. В данном случае нас интересует фотография процесса: мы рассматриваем изменение деформации вдоль стержня в заданный момент «остановленного» времени.

В результате деформации стержня в его сечении возникают упругие силы, интенсивность которых принято характеризовать напряжением:

Согласно закону Гука напряжение в любом сечении стержня пропорционально относительной деформации ε:

σ = E ε.

Здесь E — модуль упругости (Юнга).

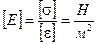
Теперь запишем основное уравнение динамики для выделенного элемента стержня :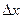

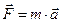
Рис. 2.1

	x

Рис.2.1

В этом уравнении:

,

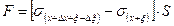- масса выделенного элемента,

- его ускорение.

Распишем по – подробнее упругую силу, действующую вдоль оси стержня.

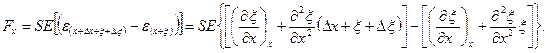
Таким образом

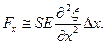
Теперь уравнение второго закона Ньютона можно привести к следующему виду:

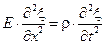. (2.2)

Или записать его так:

. (2.3)

Сравним этот результат с уравнением (2.1).

Понятно, что полученный нами результат (2.3) — классическое дифференциальное волновое уравнение.

Отсюда как минимум два вывода:

1. Нанося удар по стержню, мы возбуждаем в нём волновой процесс.

2. Скорость распространения такой продольной волны в стержне

определяется только его материалом: плотностью (ρ) и модулем упругости (E).

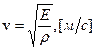(2.4)