Точность вычисления погрешностей
Как уже говорилось, средняя квадратичная погрешность характеризует реальную ошибку опыта лишь по порядку величины. Поэтому точное вычисление самих погрешностей не имеет особого смысла и при расчетах величины ошибки достаточно ограничиться одной – двумя значащими цифрами. Например, такая запись результатов измерений какой-либо величины: x =2,8674±0,0706 бессмысленна. Величину ошибки следует писать либо: Dx= 0,07, либо Dx=0,071.
Поэтому и при записи среднего значения следует ограничиться двумя-тремя цифрами после запятой, округляя до нужных цифр результат: 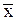 =2,87, или
=2,87, или 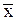 =2,867 и окончательный результат записать так:
=2,867 и окончательный результат записать так:
x=2,87 ±0,07, либо x=2,867 ±0,071.
В данном примере, впрочем, первая запись является более предпочтительной. Дело вот в чем. Давайте оценим относительную погрешность нашего результата:
ex=0,07/2,87=0,025.
Полученный результат означает, что погрешность составляет сотые доли нашего результата. Тем самым, трех значащих цифр достаточно для его записи. Отсюда можно сделать вывод, что количество значащих цифр в результате определяется относительной погрешностью ваших измерений.
Остановимся еще на таком вопросе, – как записывать приближенные значения очень больших или очень малых чисел? Например, мы измерили коэффициент теплового расширения тела a и нашли, что он равен 0,0000163 град-1, а его относительная погрешность, например, ea= 3%. При такой относительной погрешности, как мы видели, следует оставить только три значащих цифры, а их как будто никак не меньше шести. Что делать? Ответ такой – надо записать результат с помощью степеней числа 10, оставив нужное количество значащих цифр:
a=(1,63±0,05)×10–5 град-1.
Все расчеты с приближенными числами следует проводить с точностью несколько превосходящей точность измерений, чтобы избежать дополнительных ошибок, связанных с неточностью вычислений. При вычислении обычно сохраняют на один знак больше, чем будет оставлено в окончательном ответе.
Следует при расчете ошибок по формулам иметь в виду еще одно обстоятельство. Зачастую слагаемые, входящие в правые части этих формул, имеют разные порядки величин. Поскольку расчет ошибок носит, в основном, оценочный характер, то для оценки часто бывает достаточно учитывать в этих формулах лишь те слагаемые, которые имеют наибольший порядок величины, и все остальные слагаемые, малые по сравнению с первыми, просто отбрасывать. Рассмотрим в связи с этим вновь пример определения плотности r. Ошибка Dr дается формулой:
 .
.
Если при измерении массы тела вы пользовались аналитическими весами, на которых масса тела определяется с точностью до 10-4 г, а для определения объема измеряли линейные размеры тела, скажем, штангенциркулем, который дает точность до 0,1 мм, то в случае, если m»1-10 г, V»1 см3 получим:
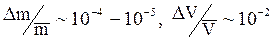 .
.
Ясно, что главную роль будет играть погрешность в определении объема, поэтому погрешность в определении массы можно положить равной нулю и полагать: 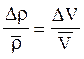 .
.
Правила округления результатов и погрешностей измерений
Погрешности измерений сами определяются с некоторой ошибкой.
Эта погрешность погрешности обычно такова, что в окончательном результате погрешность приводят всего с одной- двумя значащими цифрами.
Результат измерения принято округлять так, чтобы числовое значение результата оканчивалось цифрой того же разряда, что и значение погрешности. Следует помнить порядок, что сначала округляется погрешность, затем сам результат измерений.
Пример. Пусть получен результат измерений l = 67132 ± 4651 м для P = 0,95. Запись в таком виде неприемлема, так как претендует на чрезмерную точность и лишена наглядности. Правильная запись: l =(6,7± 0,5) · 104 м, для P = 0,95 (см. также табл. 4).
Таблица 4
Правила округления
| До округления | После округления | Пояснение |
| 734,7 | 4<5 | |
| 6>5 | ||
| 735,0 | 3 – нечетное | |
| 745,0 | 4- четное | |
| 745,1 | После 5 не нуль |
Дата добавления: 2015-08-04; просмотров: 1212;
