Ситуация (систематическая погрешность много меньше случайной)
Предположим, что погрешности приборов малы и ими можно пренебречь по сравнению со случайными погрешностями. В этом случае случайная погрешность доминирует и порядок нахождения ошибки следующий.
1. Определяется среднее арифметическое ряда n одинаковых измерений (в теории вероятности и теории ошибок доказывается, что оно является наиболее вероятным значением измеряемой величины):
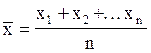 .
.
2. Вычисляется случайная абсолютная погрешность каждого (или единичного) измерения:
Δxi = 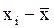 ,
,
где номер i меняется от 1 до n (или часто пишут i=1,2…n).
3. Находятся квадраты погрешностей каждого измерения и их сумма:
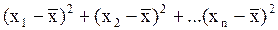 .
.
4. Вычисляется средняя квадратическая погрешность единичного измерения:
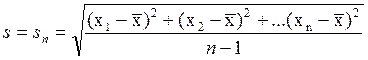 . (1)
. (1)
Причем при больших n®¥ средняя квадратическая погрешность s стремиться к генеральной средней квадратической погрешности s и формула (1) переходит в:
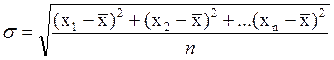 .
.
5. Вычисляется средняя квадратическая погрешность среднего значения:
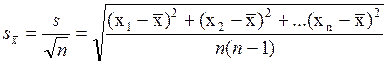 . (2)
. (2)
При больших n®¥ средняя квадратическая погрешность 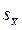 среднего значения также стремиться к генеральной средней квадратической погрешности
среднего значения также стремиться к генеральной средней квадратической погрешности 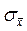 и формулу (2) часто записывают в виде:
и формулу (2) часто записывают в виде:
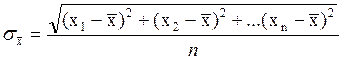 . (3)
. (3)
6. Результаты измерений записываются в виде:
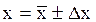 . (4)
. (4)
Такая запись означает, что точное значение измеренной величины лежит внутри интервала ( 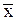 –Dx,
–Dx, 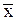 +Dx), причем полуширина интервала равна
+Dx), причем полуширина интервала равна 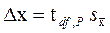 , где tdf, P - некоторый коэффициент.
, где tdf, P - некоторый коэффициент.
Если число измерений n<30 невелико, то коэффициент tdf, P , называемый коэффициентом Стьюдента, зависит от степеней свободы df=n-1 и доверительной вероятности P (см. табл. 1). Если число измерений велико или (n®¥) стремиться к бесконечности, то tdf, P зависит только от доверительной вероятности P.
Поскольку интервал ( 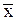 –Dx,
–Dx, 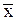 +Dx) зависит от доверительной вероятности P, то его называют доверительным. Причем, говорят, что, абсолютная погрешность сделанных нами измерений с вероятностью P не превышает Δx.
+Dx) зависит от доверительной вероятности P, то его называют доверительным. Причем, говорят, что, абсолютная погрешность сделанных нами измерений с вероятностью P не превышает Δx.
Например, если n=50 и P=0,68, то tdf, P»1, поэтому 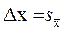 и внутри этого интервала точное значение измеренной величины лежит с вероятностью P=0,68, т.е. в 68 случаях из 100 точное значение измеренной величины лежит в этом интервале. Если рассмотреть интервал (
и внутри этого интервала точное значение измеренной величины лежит с вероятностью P=0,68, т.е. в 68 случаях из 100 точное значение измеренной величины лежит в этом интервале. Если рассмотреть интервал ( 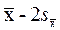 ,
, 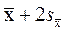 ), то точное значение измеренной величины окажется внутри него с вероятностью P=0,95, а для интервала (
), то точное значение измеренной величины окажется внутри него с вероятностью P=0,95, а для интервала ( 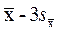 ,
, 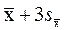 ) эта вероятность равна P=0,997.
) эта вероятность равна P=0,997.
Таблица 1
Коэффициенты Стьюдента tdf, P для различных степеней свободы df и
доверительных вероятностей P = 0,68; 0,90; 0,95; 0,99; 0,999
| Р =0,68 | Р =0,90 | Р =0,95 | Р =0,99 | Р= 0,999 | |
| df=n-1 | |||||
| 1,8190 | 6,3138 | 12,7062 | 63,6567 | 636,6192 | |
| 1,3116 | 2,9200 | 4,3027 | 9,9248 | 31,5991 | |
| 1,1889 | 2,3534 | 3,1824 | 5,8409 | 12,9240 | |
| 1,1344 | 2,1318 | 2,7764 | 4,6041 | 8,6103 | |
| 1,1037 | 2,0150 | 2,5706 | 4,0321 | 6,8688 | |
| 1,0840 | 1,9432 | 2,4469 | 3,7074 | 5,9588 | |
| 1,0703 | 1,8946 | 2,3646 | 3,4995 | 5,4079 | |
| 1,0602 | 1,8595 | 2,3060 | 3,3554 | 5,0413 | |
| 1,0525 | 1,8331 | 2,2622 | 3,2498 | 4,7809 | |
| 1,0464 | 1,8125 | 2,2281 | 3,1693 | 4,5869 | |
| 1,0415 | 1,7959 | 2,2010 | 3,1058 | 4,4370 | |
| 1,0374 | 1,7823 | 2,1788 | 3,0545 | 4,3178 | |
| 1,0340 | 1,7709 | 2,1604 | 3,0123 | 4,2208 | |
| 1,0311 | 1,7613 | 2,1448 | 2,9768 | 4,1405 | |
| 1,0285 | 1,7531 | 2,1314 | 2,9467 | 4,0728 | |
| 1,0263 | 1,7459 | 2,1199 | 2,9208 | 4,0150 | |
| 1,0244 | 1,7396 | 2,1098 | 2,8982 | 3,9651 | |
| 1,0227 | 1,7341 | 2,1009 | 2,8784 | 3,9216 | |
| 1,0212 | 1,7291 | 2,0930 | 2,8609 | 3,8834 | |
| 1,0198 | 1,7247 | 2,0860 | 2,8453 | 3,8495 | |
| 1,0186 | 1,7207 | 2,0796 | 2,8314 | 3,8193 | |
| 1,0174 | 1,7171 | 2,0739 | 2,8188 | 3,7921 | |
| 1,0164 | 1,7139 | 2,0687 | 2,8073 | 3,7676 | |
| 1,0155 | 1,7109 | 2,0639 | 2,7969 | 3,7454 | |
| 1,0146 | 1,7081 | 2,0595 | 2,7874 | 3,7251 | |
| 1,0112 | 1,6973 | 2,0423 | 2,7500 | 3,6460 | |
| 1,0044 | 1,6759 | 2,0086 | 2,6778 | 3,4960 | |
| 0,9994 | 1,6602 | 1,9840 | 2,6259 | 3,3905 | |
| 0,9969 | 1,6525 | 1,9719 | 2,6006 | 3,3398 | |
| ¥ | 0,9945 | 1,6449 | 1,9600 | 2,5758 | 3,2905 |
Поэтому, если в процессе измерений, вы получили результат, отличающийся от среднего на величину большую тройной ошибки, то такое измерение может быть отброшено, как заведомо неверное. Точнее говоря, вероятность появления такого результата равна 1– 0,997=0,003.
Посмотрите также на рис. 1, где показана плотность вероятности распределения Стьюдента стандартизованной случайной величины (s=s=1) в зависимости от коэффициента tdf, P. Очевидно (см. рис. 1), что при tdf, P =0 измеряемая величина равна среднему значению x= 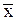 и здесь плотность вероятности максимальна, далее симметрично влево и вправо эта плотность уменьшается. Заметим, что при n®¥ или df®¥ распределение Стьюдента переходит в распределение Гаусса (или нормальный закон распределения).
и здесь плотность вероятности максимальна, далее симметрично влево и вправо эта плотность уменьшается. Заметим, что при n®¥ или df®¥ распределение Стьюдента переходит в распределение Гаусса (или нормальный закон распределения).
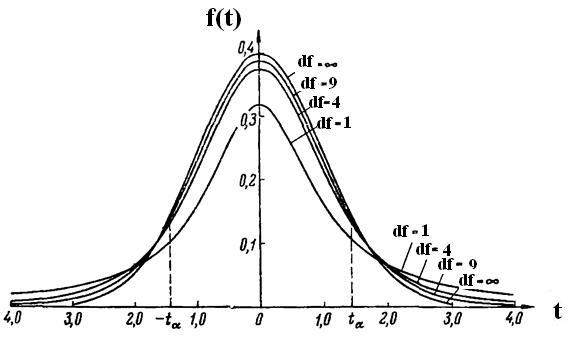
Рис. 1. Плотность вероятности распределения Стьюдента f(t) для различных степеней свободы df в зависимости от коэффициента 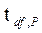 (при s=s=1).
(при s=s=1).
Относительная погрешность (случайных величин) находится как:
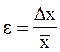 , (5)
, (5)
может быть выражена либо в долях, скажем, e=0,01, либо в процентах e=1%.
Пример. Обработаем результаты четырех (n = 4) измерений массы тела.
Таблица 2
| № | ||||
| M | 1,87 | 1,97 | 1,86 | 2,23 |
Среднее для них 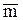 = 1,98 кг. Полуширину доверительного интервала (погрешность среднего) вычислим по формуле (4):
= 1,98 кг. Полуширину доверительного интервала (погрешность среднего) вычислим по формуле (4):
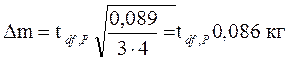 .
.
Задав доверительную вероятность P = 0,95, из табл. 1 для df = n-1 = 3,
найдем tdf, P = 3,18. Тогда Dm = 3,18 · 0,086 = 0,28 кг. Результат измерения m = 1,98±0,28 кг. Округлив его по правилам, изложенным ниже, получим
результат в окончательном виде m= 2,0 ± 0,3 кг при P = 0,95.
Формула (3) показывает, что с ростом числа измерений погрешность будет уменьшаться как 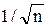 , поскольку
, поскольку
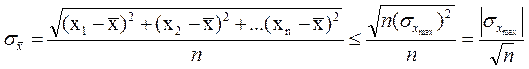 ,
,
а величина sXmax– ограниченная.
Не следует, однако, думать, что увеличивая n, вы тем самым можете сделать ошибку измерений сколь угодно малой. Увеличивая n, вы уменьшите лишь случайную ошибку, систематическую же ошибку вы при этом изменить не можете. В теории вероятностей показывается, что полная ошибка:
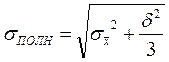 , (6)
, (6)
где d – погрешность прибора (или инструментальная погрешность), 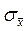 – средняя квадратичная погрешность.
– средняя квадратичная погрешность.
Поэтому не следует производить очень много измерений, если заведомо известно, что точность измерительных приборов невысока.
Дата добавления: 2015-08-04; просмотров: 1474;
