Определение погрешностей при косвенных измерениях

В большинстве случаев при проведении физических экспери­ментов исследуемая физическая величина не может быть измерена непосредственно, а является функцией одной или нескольких пе­ременных, измеренных непосредственно. Определение поверхност­ного натяжения (s = F/l), вязкости жидкости с помощью виско­зиметра (h=h_o[rt /(r₀t₀)]), концентрации раствора сахара поля­риметрическим методом (С = jkl)), так же как и определение очень многих других физических величин, производится с по­мощью косвенных измерений.

Погрешности для величин, которые входят в формулу расчета искомой величины и которые определяются прямыми измерения­ми, рассчитываются по правилам расчета погрешностей при пря­мых измерениях. Исходя из этих погрешностей и функциональной зависимости (формулы физического закона), связывающей изме­ряемые величины с вычисляемой, необходимо определить погреш­ность определяемой величины (например, s, h, С и др.).

Использование формул дифференцирования

Для определения абсолютных и относительных погрешностей искомой величины при косвенных измерениях можно воспользоваться формулами дифференцирования, так как формулы погреш­ностей получаются в том же приближении, что и формулы для дифференциала функции.

Так, например,

Δ(uv) = (u+ Δu) (v+ Δv)—uv=uv+ Δuv+ Δvu+ ΔuΔv—uv» Δuv+uΔv,

поскольку ΔuΔv — бесконечно малая более высокого порядка и ею можно пренебречь. С другой стороны, d(uv) =duv+ udv, a dudv пренебрегаем.

Таким образом, погрешности можно находить по формулам вычисления дифференциалов функции.

Для нахождения погрешностей величины, являющейся функцией других величин, u=f(x₁, x₂, … ,x_m) необходимо:

а) найти полный дифференциал функции,

,

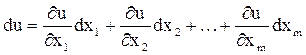б) определить абсолютную погрешность, заменив знак дифференциала d на знак абсолютной погрешности Δ и подставляя в формулу,

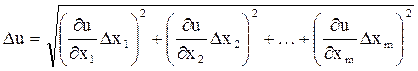. (7)

Заметим, что складываются не сами средние квадратические погрешности, а их квадраты (дисперсии).

в) вычислить относительную погрешность измерения искомой величины .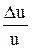

Например, для некоторых частных случаев имеем:

Таблица 3

Вычисление косвенных погрешностей

Функция	Относительная погрешность
z=x±y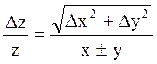
z=xy или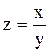
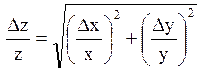
z=xmyn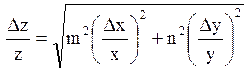
z= ln (x)
z= ex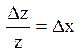

Так, из табл. 3 получим, что для определения плотности тела правильной формы измерили массу 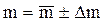, объем 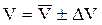, тогда 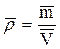, а относительная погрешность плотности равна .

Точность при косвенных измерениях

В эксперименте при косвенных измерениях выбор приборов зависит от требуемой точности измерения. Однако нередко бывают случаи, когда приходится измерять различные физические величины с различной точностью. В этом случае при оценке общей точности измерения следует ориентироваться на ту из величин, которая определяется с наибольшей погрешностью.