Лабораторная работа № 1

Тема: «Измерение линейных величин»

Значение темы:

Тема «Измерение линейных величин» является основополагающей при изучении практической физики.

Цели работы:

1) Ознакомится с методами измерения линейных величин

2) Научится использовать штангенциркуль и микрометр

3) Ознакомиться с методами обработки экспериментальных данных и оценки точности измерений.

Оборудование:штангенциркуль, микрометр, измеряемые тела.

План изучения темы:

Контроль исходного уровня знаний.

- тестирование;

- индивидуальный устный опрос, фронтальный опрос.

Основные понятия и положения темы

Нониус

Нониусом называют дополнение к обычному масштабу, позволяющее повысить точность измерения с данным масштабом в 10-20 раз.

Линейный нониус - это маленькая линейка, которая может скользить вдоль большой линейки, называемой масштабом. Деления на нониусе наносятся обычно так, что одно деление нониуса составляет (m - 1)/m= 1 - 1/m часть делений масштаба, где m- число делений нониуса.

Рис. 1. Линейный нониус.

Аналогичным образом можно строить не только линейные, но и угловые нониусы. Нониусами снабжаются штангенциркули (рис. 2), теодолиты и многие другие приборы.

Штангенциркуль

Штангенциркуль (рис. 2) имеет, кроме основных делений на штанге, вторую шкалу делений — нониус по внутреннему краю рамки. Если ножки прибора плотно сомкнуты, начальные деления обеих шкал совпадают; при этом легко заметить, что девяти делениям основной шкалы (а) соответствуют десять делений нониуса (b).

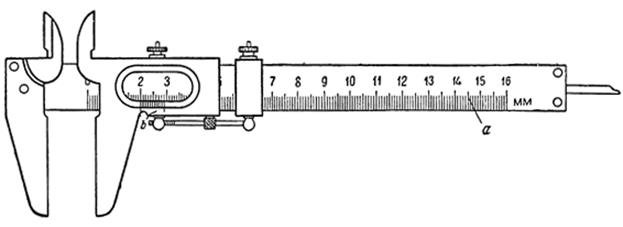
Рис. 2. Штангенциркуль.

Каждое деление нониуса равно 0,9 деления основной шкалы. Таким образом, разница между делениями основной шкалы и делениями нониуса составляет 0,1 деления основной шкалы.

Рассмотрим примерную процедуру измерения с помощью увеличенной модели нониуса на рисунке 3.

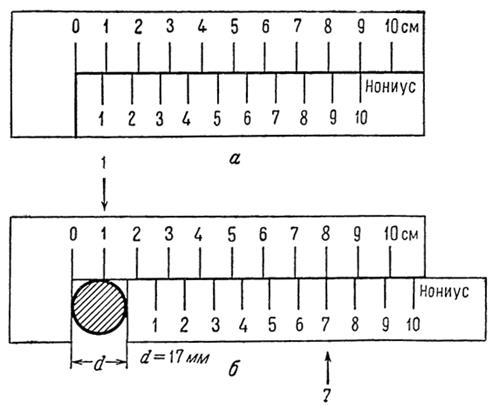
Рис. 3 . Модель нониуса и ход измерений:

а — нулевое положение; б — схема измерения.

Переведя нониус (рис. 3, а) в положение, при котором его нулевое деление совпадает с нулевым делением основной шкалы, легко обнаружить разницу в 0,1 см на каждом сантиметре основной шкалы. При всех перемещениях нониуса одно из его делений будет совпадать с каким-то из делений основной шкалы. Чтобы определить искомый размер, достаточно посмотреть, какое деление нониуса совпало с делением основной шкалы, и установить его порядковый номер. Это даст число десятых долей деления основной шкалы. На рисунке 3 б дано измерение диаметра валика. Легко установить, что величина диаметра лежит между 1 и 2 см. Так как 7-е деление нониуса совпадает с одним из делений основной шкалы, в нашем случае с 8-м, то искомый измеряемый диаметр d = 1,7 см.

Микрометрический винт. Микрометр.

При точных измерениях расстояний нередко применяют микрометрические винты – винты с малым и очень точно выдержанным шагом. Такие винты употребляются, например, в точных измерительных приборах (микроскоп, микрометр) и позволяет проводить измерения до сотых долей миллиметра. (рис. 4). Один поворот винта микрометра передвигает его стержень на 0,5 мм. Барабан, связанный со стержнем, разбит на 50 делений. Поворот на одно деление соответствует смещению стержня на 0,01 мм. С этой точностью обычно и производятся измерения с помощью микрометра. Микрометрический винт представляет собой стержень, снабженный точной винтовой нарезкой.

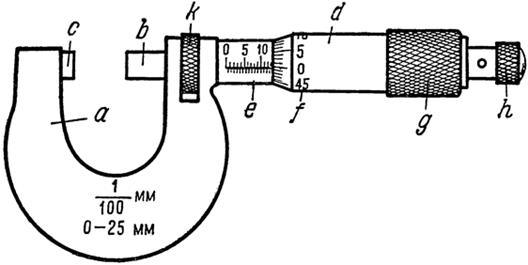
Рис. 4. Микрометр. а — скоба; b — измерительная головка; с — пятка; d — барабан с лимбом (круговая шкала); е — стебель с миллиметровой шкалой; f — лимб с отсчетом до 0,01 мм; g — рифленый барабан; h — трещотка, k— стопор.

Высота подъёма винтовой нарезки за один оборот называется шагом микрометрического винта. Микрометр (рис. 4) состоит из двух основных частей: скоба a и микрометрический винт (измерительная головка) b. Микрометрический винт проходит через отверстия скобы с внутренней резьбой, против микрометрического винта на скобе имеется упор (или пятка). На микрометрическом винте закреплен полный цилиндр (барабан) с делениями по окружности. При вращении микрометрического винта барабан скользит по линейной шкале, нанесенной на стебле.

Для того, чтобы микрометрический винт b передвинулся на 1 мм, необходимо сделать два оборота барабана d. Таким образом, шаг микрометрического винта равен 0,5 мм. У микрометра на барабане d имеется шкала (лимб), содержащая обычно 50 делений. Так как шаг винта s=0,5 мм, а число делений барабана m =50, то точность микрометра составляет

s/m = 0,5/50 = 1/100 мм. (1)

В итоге, числовое значение длины измеряемого предмета микрометром или штангенциркулем находят

L = q s + n s/m, (2)

где q- целое число мм масштабной линейки,n– деление нониуса, которое совпадает с любым делением масштабной линейки, s/m –точность.

Результат можно сформулировать следующим образом: длина образца, измеряемая с помощью нониуса, равна числу целых делений масштаба плюс точность нониуса, умноженная на номер деления нониуса совпадающего с некоторым делением масштаба.