Плоская электромагнитная волна

Под плоской электромагнитной волной понимают волну вектора напряженности электрического поля и магнитного поля, которые расположены в плоскости перпендикулярно направлению распространения волны и изменяются только в функции координаты z и времени t.

В дальнейшем под плоской электромагнитной волной будем понимать плоскую линейно - поляризованную волну, вектор напряженности электрического поля которой направлен по оси Х, а вектор напряженности магнитного поля по Y.

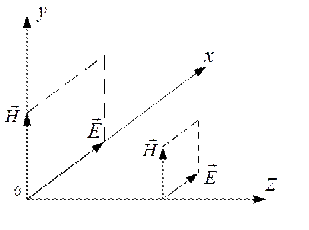
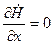
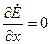
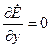
Совместим мнимую ось с осью Y, получим, что:

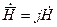
Решим уравнение для плоской электромагнитной волны.

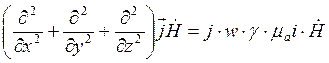
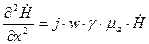- дифференциальное уравнение второго рода.

Решение дифференциального уравнения второго рода в общем виде

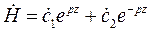
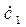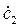, - постоянные интегрирования определяются из граничных условий.

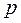- постоянная распространения электромагнитной волны.

Найдем постоянную распространения из характеристического уравнения

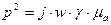
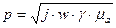
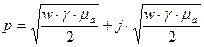
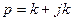, где

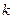- коэффициент затухания

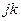- коэффициент фазы

Найдем напряженность электрического поля из первого уравнения Максвелла

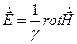
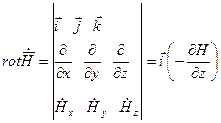
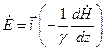
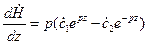
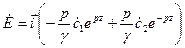
Единичный орт i говорит о том, что вектор напряжённости электрического поля направлен вдоль оси Х.

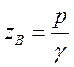- волновое сопротивление.

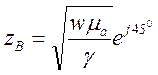[Ом] зависит от свойств среды и угловой частоты

Проекция вектора напряженности электрического поля на ось «х» равна:

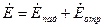
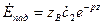
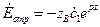
Проекция вектора напряженности магнитного поля на ось «у» равна:

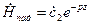
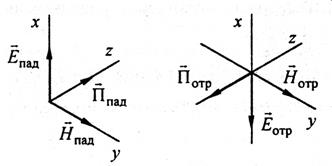
Найдем направление вектора Пойнтинга