Лекция 7. Электромагнитная индукция. Явление самоиндукции. Индуктивность. Трансформатор
В 1831 г. М.Фарадей обнаружил, что в замкнутом проводящем контуре при всяком изменении потока вектора В через поверхность, ограниченную этим контуром, возникает электрический ток. Это явление было названо электромагнитной индукцией, а возникающий ток - индукционным. Появление индукционного тока свидетельствует о наличии электрического поля, вызванного изменением магнитного потока во времени. Направление индукционного тока подчиняется следующему правилу.
Правило Ленца. Индукционный ток направлен так, чтобы противодействовать своим магнитным полем вызывающей его причине.
Закон электромагнитной индукции Фарадея-Ленца математически формулируется следующим образом:
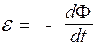 .
.
При изменении потока магнитной индукции через замкнутый контур в последнем возникает эдс электромагнитной индукции, пропорциональная скорости изменения магнитного потока через поверхность, ограниченную этим контуром.
|
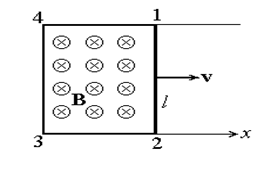
| Рис.27 |
Поместим контур с подвижной перемычкой длиной l (рис.27) в однородное магнитное поле В, перпендикулярное плоскости листа. Пусть перемычка движется вправо со скоростью v. Очевидно, с такой же скоростью будут перемещаться и носители зарядов (электроны) в перемычке. С точки зрения неподвижного наблюдателя на эти заряды должна действовать сила Лоренца
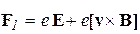 ,
,
или в скалярном виде
F1 = eE - evB = eE1, где E1 = E 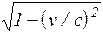 , Þ
, Þ
E1 = E - vB,
что совпадает с преобразованием Лоренца (54). Подставляя E1 в выражение, определяющее эдс ( 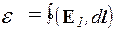 ), получим
), получим
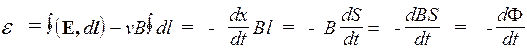 ,
,
где 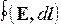 =0, как циркуляция вектора Е электростатического поля. От выражения
=0, как циркуляция вектора Е электростатического поля. От выражения 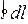 остается интеграл только на участке 1-2, так как на остальных v=0. Итак, мы пришли к закону электромагнитной индукции
остается интеграл только на участке 1-2, так как на остальных v=0. Итак, мы пришли к закону электромагнитной индукции
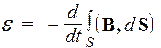 . (77)
. (77)
Единицей измерения магнитного потока Ф в СИ является вебер, [Вб], равный потоку через поверхность площадью I м2, пересекаемую перпендикулярно к ней линиями магнитного поля с индукцией в I Тл. При изменении магнитного потока со скоростью I Вб/с в контуре индуцируется эдс, равная I B.
Явление самоиндукции. Индуктивность. Электрический ток, текущий в контуре, создает магнитный поток Ф, пронизывающий этот контур. Если ток I в контуре изменяется, то согласно закону электромагнитной индукции в этом контуре должна индуцироваться эдс. Это явление называется самоиндукцией. Рассмотрим, как связаны ток I и создаваемый им поток Ф. По закону Био-Савара-Лапласа (60)

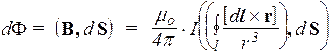 .
.
Вынесем I и проинтегрируем дважды: по границе контура l и поверхности S, ограниченной этим контуром
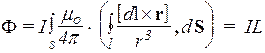 ,
,
где величина L, называемая индуктивностью, определяется только свойствами контура, в данном случае - его геометрией. Позже будет показано, что индуктивность зависит также от магнитной проницаемости m среды, которую до более строгого рассмотрения определим как отношение величины магнитной индукции в среде к магнитной индукции в вакууме. Индуктивность можно назвать коэффициентом пропорциональности между током и создаваемым им потоком в явлении самоиндукции
Ф = LI. (78)
За единицу индуктивности в 1 генри [Гн] принимается индуктивность проводника, у которого при силе тока в 1 А возникает сцепленный с ним полный поток в 1 Вб: [Гн]=[Вб/А].
Индуктивность соленоида. При прохождении тока I по длинному соленоиду в последнем возбуждается магнитное поле
B = momnI, (79)
где m - магнитная проницаемость среды, n - число витков на единицу длины. Пусть соленоид имеет площадь поперечного сечения S и полное число витков N. Тогда поток сквозь каждый виток Ф=BS, а полный поток, сцепленный с соленоидом, NФ=NBS=momnINS.Но так как N=nl, где l длина соленоида, то NФ=momn2×lS×I= =momn2×V×I, где V=Sl - объем. Следовательно, индуктивность соленоида
L = momn2×V. (80)
|
Электродвижущая сила самоиндукции. В соответствии с законом электромагнитной индукции при всяком изменении магнитного потока через проводящий контур в последнем возникает эдс. В случае самоиндукции этот поток создается изменяющимся током в самом контуре. Тогда в нем возникает эдс самоиндукции es
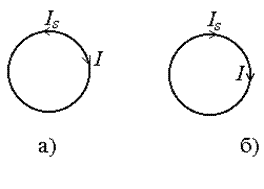
| Рис.28 |
es = 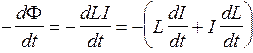 .
.
Обычно (но не всегда!) L постоянна для данного контура, и тогда
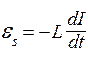 , (81)
, (81)
где минус обусловлен правилом Ленца: если основной ток I в контуре нарастает, то индукционный ток Is направлен в противоположную сторону (рис.28, а). А если основной ток I убывает, то Is направлен также как I (рис.28, б).
Взаимная индукция.Трансформатор. Пусть на один сердечник с магнитной проницаемостью m намотаны две катушки с числами витков n1 и n2 . Как будет показано ниже (см. лекцию 14), в этом случае магнитное поле будет практически полностью сосредоточено внутри сердечника. Если в катушке I течет ток I1, то он создает через катушку 2 полный магнитный поток Ф2, пропорциональный I1
Ф2 = L21I1.
При изменении тока I1, в катушке 2 индуцируется эдс
ei2 = - L21 dI1/dt.
Аналогично при протекании в катушке 2 тока I2 в катушке I возникает поток Ф1=L12I2 и. соответственно эдс индукции
ei1 = - L12 dI2/dt.
Катушки I и 2 называются связанными, а явление возникновения эдс в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности L12 и L21 называются коэффициентами взаимной индуктивности контуров. Расчет показывает, что L21= L12.
Трансформатором называется устройство, состоящее из двух связанных контуров, намотанных на общий сердечник. Он служит для повышения или понижения напряжения. В трансформаторах обе катушки охватывают одно и то же число магнитных силовых линий, поэтому величина dФ/dt для них одинакова. Считая, что поток пронизывает N1 витков в первой катушке и N2 - во второй, получим соответствующие эдс
ei2 = - N2 dФ/dt; ei1 = - N1 dФ/dt.
Следовательно,
 .
.
Таким образом, если к первой обмотке приложена ei1~U1., то, изменяя число витков N2 во второй обмотке можно получить повышенное или пониженное напряжение U2.
Токи Фуко. Индукционные токи, возбуждаемые в сплошных проводниках, называются токами Фуко. Поскольку сопротивления массивных проводников малы, токи Фуко могут достигать весьма больших величин, что приводит к значительному нагреву, например, в сердечниках трансформаторов. Для уменьшения токов Фуко сердечники набирают из тонких пластин, разделенных изолирующими прокладками. Пластины располагают перпендикулярно возможным направлениям токов Фуко.
Дата добавления: 2015-08-08; просмотров: 2416;
