Магнитный поверхностный эффект
Рассмотрим стальной лист, толщина которого много меньше высоты. Вдоль листа идет переменный магнитный поток.
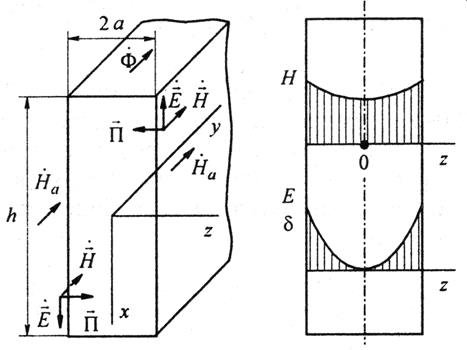
Так как 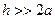 , то искажающим влиянием краев листа пренебрегаем и считаем, что в лист с 2-х сторон проникает плоская электромагнитная волна. Примем, как и прежде,
, то искажающим влиянием краев листа пренебрегаем и считаем, что в лист с 2-х сторон проникает плоская электромагнитная волна. Примем, как и прежде, 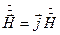 Общее решение для комплекса действующего значения
Общее решение для комплекса действующего значения 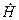 таково:
таково:
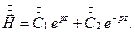
Из граничных условий найдем постоянные интегрирования. При z = - а, т. е. для точек, находящихся на левой стороне листа,
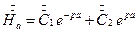
при z=+a 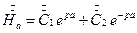 .
.
Совместное решение системы 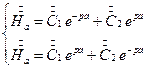 относительно C1 и С2 дает
относительно C1 и С2 дает 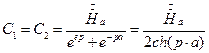 .
.
Следовательно, в произвольной точке
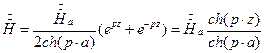 .
.
Напряженность электрического поля
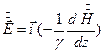 , где
, где 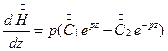
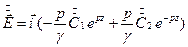
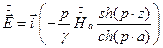
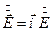 .
.
При z=+a напряженность 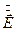 направлена вдоль оси - х; при z = -а - вдоль оси +х. Вектор Пойтинга направлен внутрь листа.
направлена вдоль оси - х; при z = -а - вдоль оси +х. Вектор Пойтинга направлен внутрь листа.
Ток, возникающий при прохождении по листу переменного магнитного потока, принято называть вихревым.
Вектор плотности вихревого тока 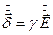 в любой точке листа коллинеарен с вектором
в любой точке листа коллинеарен с вектором 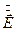 в этой же точке. Поэтому график распределения плотности вихревого тока по плоскости листа будет такой же, как и у напряженности электрического поля.
в этой же точке. Поэтому график распределения плотности вихревого тока по плоскости листа будет такой же, как и у напряженности электрического поля.
Магнитная индукция в произвольной точке
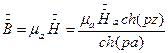 .
.
Среднее значение магнитной индукции в листе
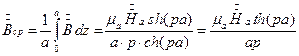 .
.
Зная, что 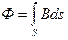 ,получаем
,получаем 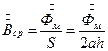
Можно найти напряженность поля на поверхности листа:
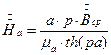
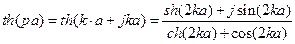
Отношение среднего значения магнитной индукции по сечению листа 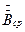 к напряженности поля на поверхности листа
к напряженности поля на поверхности листа 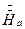 называют комплексной магнитной проницаемостью.
называют комплексной магнитной проницаемостью.
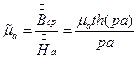
Она зависит от величины 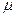 , частоты
, частоты 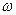 и толщины листа. При
и толщины листа. При  получаем, что
получаем, что 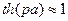 и комплексная магнитная проницаемость
и комплексная магнитная проницаемость 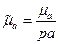 .
.
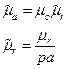
При наличии поверхностного магнитного эффекта магнитная проницаемость материала уменьшается и тем больше, чем выше частота. При очень высоких частотах магнитный поток и вихревые токи вытесняются на поверхностный слой.
Найдем
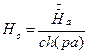
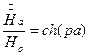
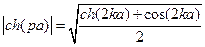
Таким образом, из последней формулы видно, что напряженность поля в средней плоскости листа может быть во много раз меньше, чем на краях.
Дата добавления: 2015-07-30; просмотров: 1254;
