Плоская электромагнитная волна в однородном проводящем полупространстве

Рассмотрим вопрос о распространении плоской электромагнитной волны в однородной проводящей среде, простирающейся теоретически в бесконечность.

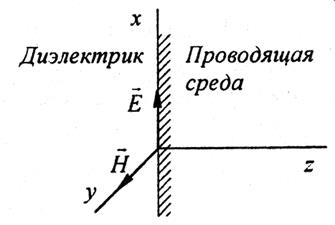
Электромагнитная волна проникает из диэлектрика в проводящую среду и распространяется в последней. Так как среда простирается теоретически в бесконечность и падающая волна в толще проводящей среды не встречает границы, которая «возмутила» бы ее распространение, то отраженной волны в данном случае не возникает.

При наличии только одной падающей волны

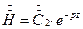и

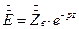
Постоянную интегрирования С₂, найдем из граничных условий. Если обозначить

напряженность магнитного поля на поверхности проводящей среды через 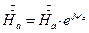, то при z = 0

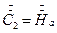
Поэтому с учетом того, что p=k(1+j) получаем

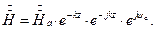
В свою очередь

.

Чтобы записать выражения для мгновенных значений Н и Е, необходимо правые части данных уравнений умножить на 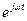и взять мнимые части от получившихся произведений.

Получим:

и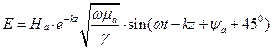

Проанализируем полученные выражения. Амплитуда Н равна 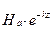. Амплитуда Е равна 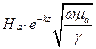. По мере увеличения Z множитель 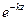уменьшается по показательному закону. Следовательно, по мере проникновения электромагнитной волны в проводящую среду амплитуды Е и Н уменьшаются по показательному закону.

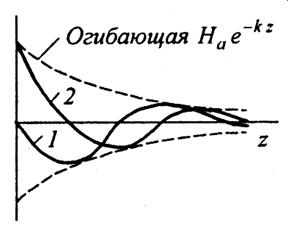
Если принять , то на графике мгновенных значений Н в функции от z будет получена кривая 1 при 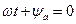и кривая 2 при .

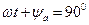Для того чтобы охарактеризовать, насколько быстро уменьшается амплитуда падающей волны по мере проникновения волны в проводящую среду, вводят понятие глубины проникновения.

Под глубиной проникновения 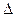понимают расстояние вдоль направления распространения волны (вдоль оси z), на котором амплитуда падающей волны Е (или Н) уменьшается 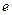раз. Глубину проникновения определяют с помощью выражения

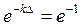
Отсюда следует, что 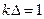или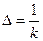

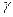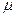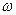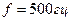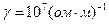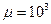Глубина проникновения зависит от свойств проводящей среды ( и ) и частоты . Так, если электромагнитная волна имеет частоту и проникает в проводящую среду, у которой и , то

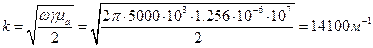
Глубина проникновения 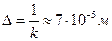, т.е. на расстоянии в 0,007 см амплитуды Н и Е снизились в 2,7183 раза.

Под длиной волны 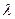в проводящей среде понимают расстояние вдоль направления распространения волны (вдоль оси z) на котором фаза колебания изменяется на 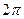. Длину волны определяют из уравнения 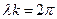, отсюда

Под фазовой скоростью понимают скорость, с которой надо было бы перемещаться вдоль оси z, чтобы колебание имело одну и ту же фазу. Фаза колебания определяется выражением 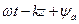. Производная от постоянной величины есть нуль, поэтому

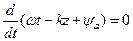или ; ;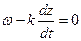

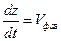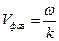
Эффект быстрого затухания широко используются на практике:

Электромагнитные экраны, нагрев металлических деталей перед ковкой, сушка древесины, наплавка и реставрация инструмента, поверхностная закалка стальных инструментов и деталей, нагрев несовершенных диэлектриков.

Экранирование в переменном электромагнитном поле.

Основано на том, что электромагнитная волна протекая в стенки экрана, быстро затухает, расходуя энергию на покрытие потерь обусловленными вихревыми токами в стенках экрана. Если экран выполнен из ферромагнитного материала, то экранирование достигается за счёт стремления силовых линий пойти по участкам с меньшим магнитным сопротивлением.