Движение материальной точки в однородном силовом поле
Силовым полемназывается пространство, в каждой точке которого на помещенную в нее материальную точку действует некоторая сила. В общем случае эта сила зависит от положения материальной точки в силовом поле и от времени, т.е.
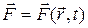 .
.
Если сила не зависит явно от времени, то силовое поле называется стационарным. Если сила, действующая со стороны силового поля на материальную точку, не зависит от положения материальной точки в силовом поле, то такое силовое поле называется однородным. Отметим, что однородное силовое поле является стационарным. В таком поле
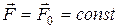 . (2.21)
. (2.21)
Рассмотрим движение материальной точки в однородном силовом поле.
На основании второго закона Ньютона (2.8) (в системе единиц СИ k=1) имеем:
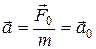 , (2.22)
, (2.22)
где 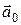 в силу условия (2.21) – постоянное по величине и направлению ускорение материальной точки.
в силу условия (2.21) – постоянное по величине и направлению ускорение материальной точки.
Пусть в некоторый момент времени t0, условно принятый за начальный, материальная точка имела относительно выбранной инерциальной системы отсчета скорость 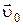 . Удобно в этом случае оси координат ориентировать, используя направления
. Удобно в этом случае оси координат ориентировать, используя направления 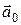 и
и 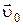 . Направим ось ОY вдоль вектора
. Направим ось ОY вдоль вектора 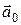 , а плоскость XОY совместим с плоскостью, в которой лежат векторы
, а плоскость XОY совместим с плоскостью, в которой лежат векторы 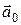 и
и 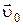 (рис. 2.5).
(рис. 2.5).
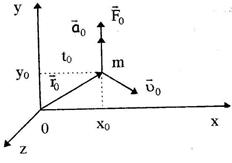 Рис. 2.5
Рис. 2.5
| При таком выборе системы координат
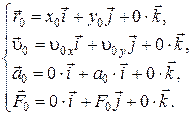 (2.23)
Используя определение ускорения (2.23)
Используя определение ускорения 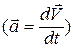 , для приращения скорости за время dt получим , для приращения скорости за время dt получим 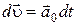 . .
|
Интегрируя последнее соотношение 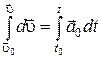 , будем иметь
, будем иметь
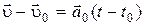 или
или 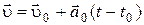 . (2.24)
. (2.24)
Из определения скорости материальной точки (1.5) элементарный вектор перемещения 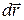 за время
за время 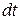 равен
равен 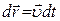 . Поэтому с учетом (2.24) и интегрирования
. Поэтому с учетом (2.24) и интегрирования
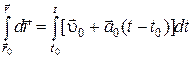
получим
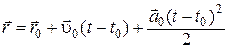 . (2.25)
. (2.25)
Движение материальной точки в однородном силовом поле полностью описывается кинематическим уравнением движения (2.25) и зависимостью скорости 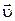 от времени t (2.24). Эти уравнения в выбранной системе координат с учетом (2.23), соответственно, примут вид
от времени t (2.24). Эти уравнения в выбранной системе координат с учетом (2.23), соответственно, примут вид
 ,
, 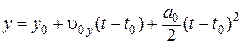 ,
,  . (2.26)
. (2.26)
Из уравнений (2.26) и (2.27) видно, что движение материальной точки происходит в одной плоскости XОY и по характеру вдоль оси ОX
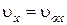 ,
, 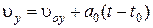 ,
, 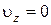 (2.27)
(2.27)
является равномерным ( 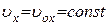 ), вдоль оси ОY – равнопеременным.
), вдоль оси ОY – равнопеременным.
Из уравнений (2.26) можно получить уравнение траектории материальной точки. Для этого исключим из них время t:
 (2.28)
(2.28)
Полученное выражение представляет собой уравнение параболы. Реальное движение, естественно, ограничено во времени и в пространстве, поэтому физический смысл имеет только конкретный участок параболы (2.28).
Примерами движения материальной точки в однородном силовом поле являются: движение частицы вблизи поверхности Земли под действием силы тяжести (h << Rз). В этом случае 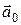 =
= 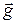 ; движение заряженной частицы в однородном электростатическом поле. В этом случае
; движение заряженной частицы в однородном электростатическом поле. В этом случае 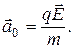
Выводы: В однородном силовом поле материальная точка движется с постоянным ускорением. Траекторией движения точки является ветвь параболы.
Ответы на контрольные вопросы
2.2. Если m1=m2 и q1=q2, то 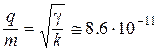 .
.
2.3. Из рис. 6.1. видно, что при отклонении нити на угол φот вертикали (υ=0), 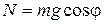 , а , а 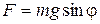 . Если при этом . Если при этом 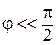 , то , то 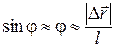 , поэтому , поэтому 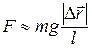 .
В пределе при .
В пределе при 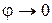 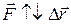 . .
| 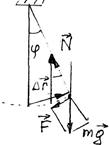 Рис. 6.1
Рис. 6.1
|
2.4. При 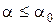 (покой),
(покой), 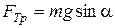 . При
. При 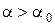 (скольжение),
(скольжение), 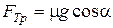 , причем при
, причем при 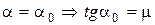 . Здесь
. Здесь 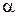 – угол наклона.
– угол наклона.
Дата добавления: 2015-08-08; просмотров: 1244;
