Локальная теорема Муавра-Лапласа.
Если в серии независимых испытаний по схеме Бернулли 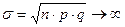 , то вероятность ровно m успехов вычисляется по следующей приближенной формуле:
, то вероятность ровно m успехов вычисляется по следующей приближенной формуле:
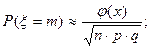
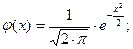
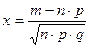
Характеристики 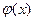 :
:
1. 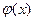 - четная:
- четная: 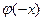 =
= 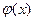 ;
;
2. 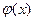 протабулирована.
протабулирована.
Задача: Из всех привитых от туберкулеза 94% приобретают иммунитет. Какова вероятность того, что среди 100 000 привитых людей 5800 не имеют иммунитета?
| Дано: | Решение: |
| n=100000 | 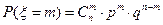
|
| m=5800 p=0,06 | 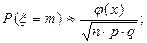
|
| P(ξ=5800)-? | 
|
 P(ξ=5800) P(ξ=5800) 
|
Задача №2
Вероятность встретить знакомого в коридоре института равна 0,2. Какое количество знакомых можно гарантировано ожидать среди 100 прохожих с вероятностью 0,095?
| Дано: | Решение: |
| n=100 p=0,2 P(ξ=m)=0,095 m-? | 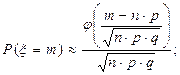
|
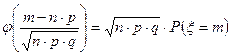

| |
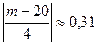
| |
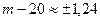
| |
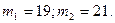
|
Дата добавления: 2015-07-30; просмотров: 1122;
