Теорема (формула) Пуассона.
Если в серии независимых испытаний по схеме Бернулли n→∞, p→0 в одном испытании;
n•p→ α, то вероятность m успехов может быть рассчитана по следующей приближенной формуле:
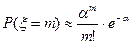
Доказательство: 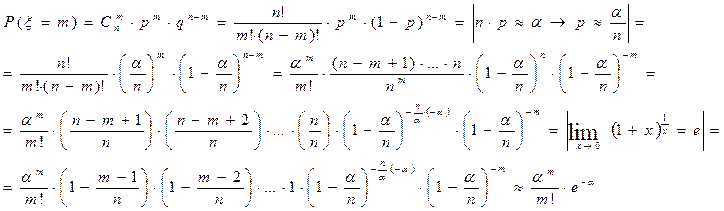 при больших n.
при больших n.
Замечание:
n~несколько десятков, то можно пользоваться формулой Пуассона
p не превышает 1/10 0≤n•p=α≤10
Пример №1
Опрашиваются 500 человек по поводу своего дня рождения (день, месяц). Какова вероятность, что ровно двое из них родились 23 октября?
| Дано: | Решение: |
| n=500 | n•p=500/365≈1,37, α≈1,37 |
| m=2 p=1/365 | P(ξ=2)= 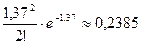
|
| P(ξ=2)-? |
Пример №2
Среди 1000 человек по статистике 8 левшей. Какова вероятность, что среди 100 случайно отобранных людей нет ни одного левши? 

| Дано: | Решение: |
| p=0,008 | 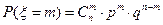
|
| n=100 m=0 | 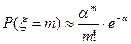
|
| P(ξ=0)-? | P(ξ=0) 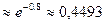
|
Дата добавления: 2015-07-30; просмотров: 1346;
