Непрерывные случайные величины.

Непрерывные случайные величины – величины, которые принимают все значения числовой оси( ).

В случае непрерывных случайных величин бессмысленно говорить о вероятности каждого его конкретного значения. Можно лишь обсуждать вероятность попадания случайной величины на некоторый промежуток числовой оси. Поэтому для описания непрерывных случайных величин вводится понятие плотности распределения вероятности р(х).

Свойства плотности вероятности:

1.

2. 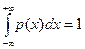- условие нормировки;

3. Вероятность попадания случайной величины ξ на [a;b] имеет следующий вид

Свойства функции распределения:

1.функция непрерывна;

2.не убывает;

3.

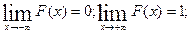
4.

5.