Случайные величины.
Опр. 1: Пусть в результате некоторого опыта происходит одно из элементарных событий 
. Числовая функция от элементарных событий 
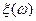называется случайной величиной.
Опр. 2: Пусть (Ω,А,Р) вероятностное пространство, тогда функция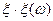 
называется случайной величиной, если 
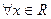множество элементарных исходов следующего вида 
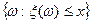является событием, т.е. оно 
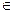А.
Опр. 3:Пусть (Ω,А,Р) вероятностное пространство. Функция 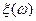называется случайной величиной, если 
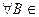ß множество элементарных исходов следующего вида 
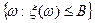является событием, т.е. оно 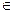А.
Пример № 1: Бросается монетка
«Орел»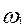 
|
«Решка»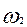 
|
| 1 | 0 | 1 |
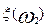
| 0 | 1 | -1 |
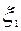
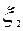
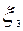
Пример № 2:Бросаем кубик
«1»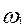 
|
| «2»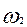
|
«3»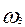 
|
«4»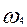 
|
«5»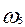 
|
«6»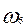 
|
|
| 1 | 1 | 1 |
|
| 2 | 1 | 2 |
|
| 3 | 2 | 1 |
|
| 4 | 2 | 2 |
|
| 5 | 3 | 1 |
|
| 6 | 3 | 2 |
Все случайные величины разделяются на 2 класса
1. дискретные
2. непрерывные
Дискретные случайные величины – это такие, которые принимают конечное и счетное множество значений.
Непрерывные случайные величины – это такие, которые принимают все значения (-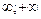 
).
Дата добавления: 2015-07-30; просмотров: 835;