Прямая задача кинематики манипуляторов
7.3.1 Постановка задачи и параметрическое описание
кинематики манипулятора
В принятых нами специальных системах координат ось zi всегда направлена: во вращательной кинематической паре по оси вращения; в поступательной кинематической паре параллельно направляющей кинематической пары.
Напомним, что положение i-го звена относительно (i-1)-го определяется обобщенной координатой qi.
Если два звена соединены вращательной парой, то при вращении i-го звена относительно (i-1)-го из четырех параметров qi, Si, аi и ai, переменным (обобщенной координатой qi) будет параметр qi, т.е. во вращательной кинематической паре (рис. 193, а): qi = qi; Si = const; ai = const; ai = const.
 Если два звена соединены поступательной парой, то при перемещении i-го звена относительно (i-1)-го из четырех параметров qi, Si, аi и ai переменным (обобщенной координатой qi) будет параметр Si, т.е. в поступательной паре (рис. 193, б):
Если два звена соединены поступательной парой, то при перемещении i-го звена относительно (i-1)-го из четырех параметров qi, Si, аi и ai переменным (обобщенной координатой qi) будет параметр Si, т.е. в поступательной паре (рис. 193, б): 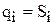 ;
;
qi = const; ai = const; ai = const.
Таким образом, из четырех параметров, ориентирующих i-ю систему координат, а следовательно, и i-е звено относительно (i-1)-го при движении i-го звена относительно (i-1)-го переменным будет один параметр qi или Si, а три остальных – постоянными.
Для описания кинематики манипулятора целесообразно использовать специальную таблицу кинематических пар, в которой для конкретного манипулятора проставляются определенные значения параметров qi, Si, аi и ai, а переменые параметры, являющиеся обобщенными координатами, отражаются буквой qi.
Таблица 3
Параметры кинематических пар
| Номер (i-1)-й кинематической пары | Тип (i-1)-й кинематической пары (вращательная или поступательная) | Номер i-го подвижного звена | Параметры кинематической пары | |||
| qi | Si | ai | ai | |||
| Вращательная | ||||||
| или | ||||||
| . | поступательная | . | ||||
| . | . | |||||
| n-1 | n | |||||
| Пример для манипулятора ВПВ (рис. 194) | ||||||
| Вращательная | q1 | |||||
| Поступательная | p | q2 | a*2 | 0,5p | ||
| Вращательная | q3 | a*3 | - 0,5p |
Примечание: a*2 и a*3 – некоторые фиксированные значения параметров a2 и a3 .
Рассмотрим порядок назначения систем координат звеньев манипулятора и определения параметров кинематических пар на примере манипулятора ВПВ (рис. 194).
Система координат O0X0Y0Z0 выбрана произвольно при обеспечении направления оси zo по оси кинематической пары Ао.
В системе координат O1X1Y1Z1 ось z1 направлена по направляющей кинематической пары А1 и совмещена с осью zo. Начало координат О1 может быть выбрано в любой точке оси z1. В нашем случае она совмещена с Оо, поэтому S1=0; ai = 0; оси zo и z1 совпадают, значит a1= 0. Так как звено 1 вращается относительно звена 0, переменным является угол q1, следовательно, q1 = q1.
Система координат O2X2Y2Z2 выбрана по ранее изложенному правилу. Так как пара А1 поступательная (звено 2 перемещается относительно звена 1), то расстояние S2 будет переменным (обобщенной координатой) S2 = q2. Величины q2, а2 и a2, найдены по общему правилу: q2 = p ; a2 = 0,5p ; a3 = a*3 . Понятно, что их значения постоянны.
Система координат O3X3Y3Z3 выбрана по правилу для n-го (последнего) звена; начало О3 координат назначено в центре схвата, ось x3 направлена перпендикулярно оси z2. Так как пара А2 вращательная, то переменным параметром будет q3 = q3 . Параметры S3, а3 и a3 определяются по общему правилу: S3 = 0; a3 = a*3 ; a3 = -1,5π и являются постоянными.
Найденные таким образом параметры манипулятора ВПВ сведены в таблицу кинематических пар (табл. 3).
Итак, нами полностью подготовлены основания для формулирования и решения прямой задачи кинематики манипуляторов.
Прямая задача кинематики манипуляторов заключается в определении положения его звеньев в неподвижной (инерциальной) системе координат по известным значениям обобщенных координат и при известных значениях параметров кинематических пар: qi, Si, аi, ai.

Частным видом прямой задачи кинематики манипулятора является определение положения его схвата, закрепленного на последнем n-м звене манипулятора. Решим эту важную задачу.
Положение схвата в неподвижной системе координат будет определено полностью, если будут известны координаты его центра и ориентация последнего n-го звена в неподвижной системе координат. В нашем случае, когда n-я система координат помещена в центр схвата, для определения положения и ориентации схвата достаточно определить координаты начала n-й системы координат и ее ориентацию в системе координат, связанной с 0-м звеном.
Запишем формулу (2) последовательно для n звеньев в порядке от звена n к звену 0.
Rn-1, n = Тn-1, n Rn, n ;
Rn-2, n = Тn-2, n-1 Rn-1, n ;
. . . . . . . . . . . . . . . .
R1, n = Т1,2 R2, n ;
R0, n = Т0,1 R1, n .
Подставив в последнее равенство последовательно все предыдущие, получим
R0,n= Т0,1 Т1,2 . . . . Тn-1, n Rn, n (6)
или в более общем виде
R0,n= Т0,n Rnn ,
где Т0,n = Т0,1 Т1,2 . . . . Тn-2, n-1 Тn-1, n . (7)
Последнее выражение (7) можно представить в матричной форме

 а110n а120n а130n а140n
а110n а120n а130n а140n
а210n а220n а230n а240n
Т 0,n = а310n а320n а330n а340n .
0 0 0 1
Обратим внимание на следующее обстоятельство: начало координат n-го звена совпадает с центром схвата, следовательно:
xnn= ynn= znn= 0 и Rn,n = 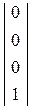 . Тогда R0n =
. Тогда R0n = 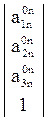 .
.
Значит, первые три элемента 4-го столбца матрицы Т0,n, а именно, элементы  представляют собой координаты центра схвата, т. е.
представляют собой координаты центра схвата, т. е.
x0,n= 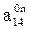 ; y0,n=
; y0,n=  ; z0,n=
; z0,n= 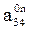 .
.
Это объясняется тем, что названные элементы являются координатами, отражающими смещение (перенос) начала n-й системы в
0-й системе координат.
Матрица Т0,n по структуре аналогична матрице Тi-1, i (см. зависимость (5)). Следовательно, 1-й элемент 2-го столбца и первые два элемента 3-го столбца будут являться направляющими косинусами осей zn и yn относительно осей x0 и y0, а именно:
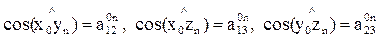 .
.
Это позволяет определить углы между соответствующими осями:
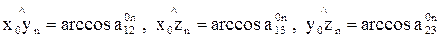 .
.
Именно эти углы применительно к звеньям i-1 и i показаны на рис. 190.
Заметим еще раз, что положение схвата в пространстве (его координаты и ориентация) определяется шестью наддиагональными элементами матрицы Тo,n. Таким образом, шесть наддиагональных элементов матрицы Тo,n дают полную информацию о положении схвата в пространстве.
Следовательно, отпадает необходимость в расчете по формуле (6), а достаточно использовать выражение (7) в виде:
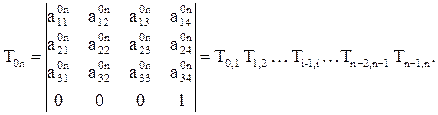 (8)
(8)
Для определения положения любого промежуточного i-го звена манипулятора относительно стойки достаточно перемножить соответствующее число первых слева матриц перехода, т.е. воспользоваться выражением, которое приводится ниже
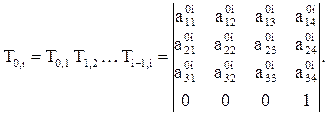
Наддиагональные элементы этой матрицы и дадут искомое решение.
Можно также определить положение любого m-го звена относительно k-го (k< m) по формуле:
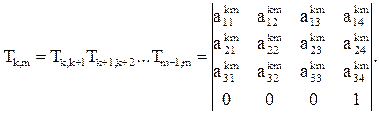
Заметим, что в силу закона ассоциативности исходные матрицы-сомножители, записанные в порядке возрастания номеров звеньев и пар манипулятора, можно перемножать как справа налево, так и слева направо.
Перемножение справа налево, видимо, более наглядно, т.к. последовательно координаты схвата пересчитываются в предыдущие системы координат. Так удобно умножать, когда определяется положение только схвата.
Перемножение слева направо позволяет попутно определить положения всех промежуточных звеньев. Для этого достаточно лишь обеспечить в ходе вычислительного процесса запоминание наддиагональных элементов матриц, получаемых как промежуточные при расчете.
Дата добавления: 2015-07-30; просмотров: 3205;
