Обратная задача кинематики манипуляторов
После того, как выполнено планирование траектории схватов в абсолютной системе координат, возникает задача определения значений обобщенных координат манипулятора по заданному в пространстве и времени положению схвата. В результате решения обратной задачи должны быть определены в аналитической или табличной форме зависимости
q1 = q1 (z0n, y0n, z0n, 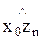 ,
, 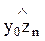 ,
, 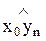 ; t);
; t);
. . .
. . .
. . .
qi = qi (z0n, y0n, z0n, 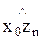 ,
, 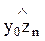 ,
, 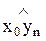 ; t);
; t);
. . .
. . .
. . .
qn = qn (z0n, y0n, z0n, 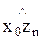 ,
, 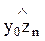 ,
, 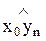 ; t).
; t).
Положение схвата во времени при работе манипулятора непрерывно меняется по заданному закону движения. При этом центр схвата должен описывать требуемую траекторию, а схват – быть ориентирован в пространстве вполне определенным образом.
Для обеспечения требуемого положения схвата в общем случае необходимо шесть степеней подвижности: три из которых – переносные – должны обеспечивать заданное положение схвата в пространстве, т.е. заданные значения координат центра схвата:
x0n = x0n (t); y0n = y0n (t); z0n = z0n (t);
а другие три – ориентирующие – заданную ориентацию схвата:
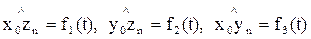 .
.
Если число степеней подвижности меньше шести, то схват не сможет занять произвольное положение в пространстве и на его положение и ориентацию будут наложены ограничения. Когда число степеней подвижности больше шести или больше заданных условий, то схват может занять требуемое положение при различных положениях промежуточных звеньев.
Избыточные степени подвижности можно использовать для удовлетворения каких-либо дополнительных условий, например, для обхода препятствий.
В дальнейшем, если специально не будет оговорено, мы будем рассматривать случаи, когда число степеней подвижности равно числу условий на положение схвата.
К настоящему времени прямого решения обратной задачи для манипуляторов общего вида не существует. В общем случае обратная задача кинематики манипуляторов решается численно.
Рассмотрим порядок решения обратной задачи с использованием методов нелинейного математического программирования, в частности, распространенного градиентного метода.
Нелинейное математическое программирование имеет следующий алгоритм:
1. Составляется или определяется критериальная функция, как функция обобщенных координат.
2. Составляется штрафная функция, выражающая дополнительные условия при решении задач и зависящая также от обобщенных координат.
3. Составляется целевая функция, в которую входят определенным образом критериальная и штрафная функции.
4. Выбирается метод нелинейного математического программирования и в соответствии с ним составляется алгоритм оптимизации критериальной функции как части целевой функции.
5. Разрабатывается расчетная программа, и производятся расчеты до выполнения определенных условий.
Изложим последовательность решения обратной задачи кинематики с использованием методов нелинейного математического программирования.
Сформируем критериальную функцию. Так как целью решения является поиск таких значений обобщенных координат, при которых разность между заданным положением схвата и его фактическим положением равнялось нулю, то в качестве критерия можно принять сумму квадратов разностей наддиагональных элементов матрицы, задающей требуемое положение схвата, и матрицы, отражающей положение схвата при текущих значениях обобщенных координат. Например:
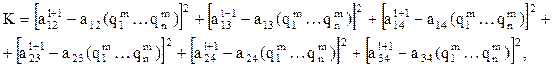 (11)
(11)
где qmi – значение i-й обобщенной координаты на m-м шаге вычислительного процесса в ходе поиска значений 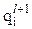 обобщенных координат соответствующих (l+1)-му положению схвата (i = 1, …, n).
обобщенных координат соответствующих (l+1)-му положению схвата (i = 1, …, n).
Функция (11) носит несколько искусственный характер. Можно предложить критериальную функцию, имеющую больший физический смысл, например, функцию 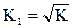 , являющуюся в некотором смысле расстоянием между заданным положением схвата и его промежуточным расчетным положением. Функция К1 приобретает строгий смысл расстояния Кr между требуемым (l+1)-м положением схвата и промежуточным расчетным, если не учитывать ориентацию схвата, а решать обратную задачу только применительно к его положению на заданной траектории:
, являющуюся в некотором смысле расстоянием между заданным положением схвата и его промежуточным расчетным положением. Функция К1 приобретает строгий смысл расстояния Кr между требуемым (l+1)-м положением схвата и промежуточным расчетным, если не учитывать ориентацию схвата, а решать обратную задачу только применительно к его положению на заданной траектории:
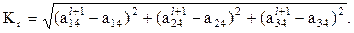
Так как перемещение по каждой степени подвижности может осуществляться только в определенных границах, то обобщенные координаты могут принимать произвольные значения в диапазпне, соответствующем этим границам: 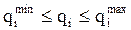 . В связи с этим для автоматического обеспечения в ходе вычислительного процесса ограничений на значения qi вводятся штрафные функции вида
. В связи с этим для автоматического обеспечения в ходе вычислительного процесса ограничений на значения qi вводятся штрафные функции вида
 0, если qi - qimin ³ 0;
0, если qi - qimin ³ 0;
Fi1 = W1i (qi min- qi), если qi - qimin < 0;

0, если qi mах - qi ³ 0;
Fi2 = W2i (qi - qi mах), если qi mах - qi < 0,
где W1i, W2i – весовые коэффициенты, которыми можно регулировать крутизну штрафных функций. Кроме указанных могут быть и другие ограничения на обобщенные координаты.
В качестве целевой функции Z можно использовать функцию, являющуюся суммой критериальной и штрафных функций, а именно:
Z(q1…qn) = K + å Fi1 + å Fi2. (i=1,…,n)
Примем в качестве метода поиска новых значений qil+1 обобщенных координат градиентный метод, выражающийся в данном случае следующей зависимостью:
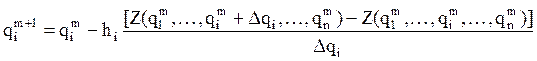 ,
,
где hi – шаг по i-й обобщенной координате; D qi – малое приращение i-й обобщенной координаты, используемое при определении частной производной по qi.
Отметим, что в качестве начального приближения qi (m=0) используется старое значение qi l, т.е. в начальный момент полагают
qi m = qi l.
Вычислительный процесс приближения к значениям qil+1 может быть прекращен по любому используемому в нелинейном программировании признаку. В частности, его можно закончить по числу шагов итерации или по условию
qi m+1 - qi m £ [di], (12)
где [di] – допустимая по точности воспроизведения траектории величина отклонения i-й обобщенной координаты.
Учитывая характер критериальной функции K, после выполнения условий (12), в качестве окончательного следует принять значение
qi l+1 = (qi m+1 + qi m) / 2.
Отметим, что (m+1)-й шаг к (l+1)-й точке траектории в процессе вычислений может осуществляться по различным алгоритмам, свойственным методам нелинейного программирования. При использовании собственного градиентного метода (m+1)-й шаг должен осуществляться одновременно по всем координатам в направлении антиградиента.
Полученные значения qil+1 обобщенных координат соотносятся с моментом времени tl+1 и запоминаются. После этого в целевую функцию Z вместо значений а12 l+1 . . . а34 l+1 подставляются значения наддиагональных элементов матрицы, соответствующей моменту времени tl+2, которые принимаются за а12 l+1 . . . а34 l+1.
Такие вычислительные циклы дожны повторяться до тех пор, пока не будут определены значения обобщенных координат для всех назначенных опорных точек l = 1, ... , L (здесь L – число заданных опорных точек на траектории движения схвата). В результате получается таблица значений обобщенных координат qi l (i = 1, ... ,n);
(l = 1, ... , L), которые можно трактовать как функции
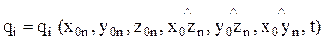 (i=1,…,n)
(i=1,…,n)
являющиеся решением обратной задачи кинематики манипулятора.
При выборе количества точек на заданной траектории возникает следующее противоречие: для более точного воспроизведения траектории желательно назначать как можно больше опорных точек, но это потребует и большего машинного времени. При небольшом количестве точек схват может отклониться от заданной траектории на недопустимую величину. Таким образом, количество необходимых опорных точек на траектории, есть функция требуемой точности воспроизведения этой траектории.
После определения в табличном виде функций qi = qi (t) можно численно их продифференцировать и найти обобщенные скорости и ускорения, возникающие в каждой степени подвижности при реализации заданной траектории схвата. Будем использовать для этого центральную разность. Тогда
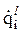 = (qil+1 - qil-1)/2Dt ;
= (qil+1 - qil-1)/2Dt ; 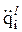 = (qil+1 - 2qil + qil-1)/Dt2 .
= (qil+1 - 2qil + qil-1)/Dt2 .
Таким образом, будут получены функции 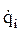 (t) и
(t) и 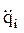 (t) также в табличном виде.
(t) также в табличном виде.
Чтобы формировать управляющие воздействия в виде непрерывных функций целесообразно аппроксимировать табличные значения обобщенных координат, скоростей и ускорений. Для этого можно воспользоваться, например, интерполяционной формулой Лагранжа.
Планирование траекторий манипулятора на основе сплайн-функций
Наиболее общим случаем планирования траектории является рассмотрение траектории движения схвата из рабочей зоны одного оборудования в рабочую зону другого.
При определении траектории должны быть учтены ограничения на саму траекторию и возможные препятствия на пути схвата.
В качестве обязательных требований обычно выступают следующие:
1. В момент снятия объекта манипулирования движение схвата должно быть направлено перпендикулярно опорной поверхности приспособления ТО до тех пор, пока схват не уйдет на безопасное расстояние. Траектория от начальной точки АН опорной поверхности до точки АУ, находящейся на безопасном расстоянии называется траекторией ухода, а сама точка АУ – точкой ухода (рис. 196).
2. В момент постановки объекта манипулирования в приспособление ТО схват, начиная с некоторого безопасного расстояния, должен подходить перпендикулярно к опорной поверхности этого приспособления. Точка АП, находящаяся на безопасном расстоянии при подходе к ТО называется точкой подхода, а траектория от этой точки до конечной точки АК – траекторией подхода (см. рис. 196).
В общем случае точки ухода и подхода, относящиеся к одному и тому же оборудованию могут не совпадать из-за наличия или отсутствия объекта манипулирования в схвате, различных габаритов и условий транспортирования заготовок и т. д.
3. Между точками ухода АУ и подхода АП схват движется в крейсерском режиме по траектории оптимальной в том или ином отношении: по быстродействию, по затратам энергии, по условиям, обеспечивающим щадящий режим транспортирования объекта манипулирования (например, могут быть ограничения на максимальные значения абсолютных скоростей и ускорений схвата).
Таким образом, в качестве наиболее общего случая следует рассматривать частную траекторию движения схвата от одной остановки до другой при его перемещении между соседними единицами ТО с выделением на ней трех характерных участков:
· участок ухода АНАУ;
· участок крейсерского перемещения АУАП от j – го ТО к (i+1) -му;
· участок подхода АПАК
и четырех характерных точек: АН, АУ, АП, АК – начальной, ухода, подхода и конечной.
Координаты этих точек первоначально должны быть заданы в системе координат 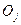
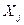

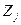 j-го ТО. Интересной задачей является выбор места расположения основания робота относительно требуемой траектории. После привязки системы координат робота к системе координат ТО координаты характерных точек АН, АУ, АП, АК должны быть пересчитаны в инерциальную систему O0X0Y0Z0 робота.
j-го ТО. Интересной задачей является выбор места расположения основания робота относительно требуемой траектории. После привязки системы координат робота к системе координат ТО координаты характерных точек АН, АУ, АП, АК должны быть пересчитаны в инерциальную систему O0X0Y0Z0 робота.

Планирование траектории манипулятора надо вести как в инерциальной системе координат робота, так и в системе его обобщенных координат. Учитывая, что управление манипулятором ведется в его обобщенных координатах 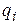 , то и планирование траекторий целесообразно вести именно в пространстве обобщенных координат.
, то и планирование траекторий целесообразно вести именно в пространстве обобщенных координат.
Возможно несколько подходов к описанию траектории АНАУАПАК в зависимости от предъявленных к ней требований:
1. Траектория на всем протяжении описывается одним полиномом по каждой обобщенной координате.
2. Каждый характерный участок траектории описывается отдельной сплайн-функцией.
3. На участках ухода АНАУ и подхода АПАК для большей определенности она задается как функция времени в инерциальных координатах робота, например, отрезком пространственной прямой. В этом случае траектория на этих участках строго определена и не подлежит планированию, а необходимо путем решения обратной задачи рассчитать соответствующие значения обобщенных координат.
4. Участок АУАП крейсерского движения схвата от одного оборудования к другому с целью получения более определенной траектории и понижения степени полиномов разбивается на более мелкие дополнительные участки.
 Реализация любого из перечисленных подходов начинается с определения значений обобщенных координат, соответствующих заданным декартовым координатам точек АНАУАПАК, путем решения обратной задачи кинематики.
Реализация любого из перечисленных подходов начинается с определения значений обобщенных координат, соответствующих заданным декартовым координатам точек АНАУАПАК, путем решения обратной задачи кинематики.
В результате будут получены четыре опорные точки в системе обобщенных координат (рис. 197):
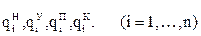
n – число подвижных звеньев манипулятора.
Задача теперь сводится к построению таких непрерывных или кусочно-непрерывных функций, которые бы проходили через указанные опорные точки, т. е. к определению функций
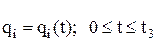 .
.
Первый подход: обобщенные траектории описываются одним полиномом. Сформируем требования, которым должна отвечать траектория в этом случае.
1. Траектория на всем протяжении должна быть гладкой.
2. Траектория должна проходить через заданные опорные точки:
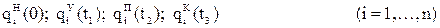
3. Скорости и ускорения схвата в начальной и конечной точках должны быть равны значениям, требуемым по условиям сопряжения схвата с технологической оснасткой. Обычно они равны нулю, однако, например, при работе с конвейером 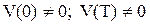 .
.
Эти требования позволяют записать граничные условия для полиномов  , исходя из которых можно получить требуемый закон движения звеньев манипулятора:
, исходя из которых можно получить требуемый закон движения звеньев манипулятора:
Точка 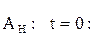
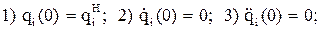
Точка 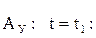
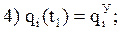
Точка 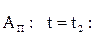
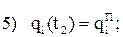
Точка 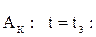
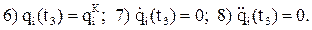
Таким образом, полином должен отвечать восьми граничным условиям и, следовательно, он должен быть минимум седьмой степени, когда в полиноме имеется восемь свободных коэффициентов. Если есть необходимость в выполнении каких-либо дополнительных условий, степень полинома может быть повышена на одну-две. Однако в общем случае такое увеличение нежелательно, т. к. при этом повышается непредсказуемость поведения траектории между опорными точками. Итак, рассмотрим полином седьмой степени.
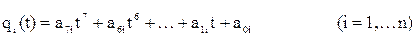
Продифференцируем его дважды:
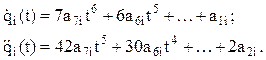
Подставим в эти выражения значения t=0 для точки АН и получим:
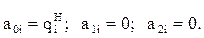
Оставшиеся пять неизвестных коэффициентов должны быть определены по пяти неиспользованным граничным условиям из системы пяти уравнений:
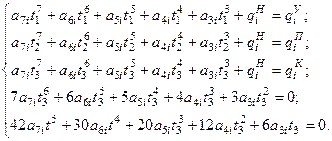
Каждый из коэффициентов полинома является функцией обобщенных координат характерных точек АН, АУ, АП, АК и интервалов времени t1, t2 и t3:
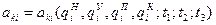 ;
; 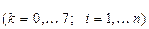 .
.
Всего должно быть определено 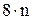 коэффициентов.
коэффициентов.
Описание траектории в пространстве обобщенных координат одним полиномом высокой степени весьма удобно с математической и алгоритмической точек зрения. Однако с физической точки зрения использование такого полинома может привести к нежелательным явлениям, а именно, к появлению эффекта “блуждания” схвата, т.е. к значительному отходу схвата от желаемой траектории (рис. 198).
В этом случае возникает сложная задача обеспечения приемлемых отклонений действительной траектории от желаемой, что можно  осуществить, отступая по возможности от принятых значений
осуществить, отступая по возможности от принятых значений 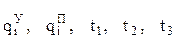 (будем считать, что координаты начальной и конечной точек qН и qК изменению не подлежат, т. к. они определяются расположением оборудования и конструкцией приспособлений.)
(будем считать, что координаты начальной и конечной точек qН и qК изменению не подлежат, т. к. они определяются расположением оборудования и конструкцией приспособлений.)
Второй подход: Чтобы уменьшить опасность нежелательного блуждания схвата стремятся использовать полиномы возможно более низких степеней. Одним из путей понижения требуемой степени полинома является представление каждого из трех участков отдельными функциями, которые на границах участка должны быть соответствующим образом сопряжены друг с другом.
В результате траектория схвата будет представлена кусочно-непрерывной функцией, составленной из трех полиномов, так называемой сплайн-функцией.
Для рассматриваемой трехучастковой траектории с целью обеспечения плавного безударного перехода с одного участка на другой функции соседних участков должны иметь равными обобщенные координаты и их первые и вторые производные.
При рассмотрении сплайн-функций вместо абсолютного времени удобно использовать относительное (нормированное) время для каждого участка
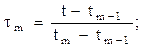
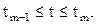
Тогда
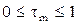 .
.
Запишем граничные условия каждого из трех участков:
| Первый участок | Второй участок | ||||
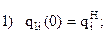
| 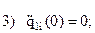
| 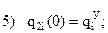
| 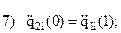
| ||
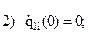
| 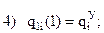
| 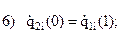
| 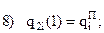
| ||
| Третий участок | |||||
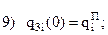
| 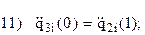
| 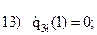
| |||
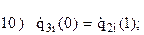
| 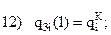
| 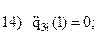
| |||
Учитывая, что используются три полинома (по одному на каждом участке) и в каждом полиноме есть один свободный коэффициент, сумма степеней полиномов должна быть равна 14-3=11 (здесь 14 – число приведенных выше граничных условий).
Известны различные комбинации степеней полинома на участках. Наибольшее распространение получили:
4-3-4 – траектории,
3-5-3 – траектории и
5-2-4 (или 4-2-5) – траектории.
Здесь цифры обозначают степени полинома соответственно на 1-м, 2-м и на 3-м участках.
Чаще других используется 4-3-4 – траектория, т. к. из всех упомянутых она состоит из полиномов более низких степеней.
Запишем аналитическое выражение для 4-3-4 – траектории:
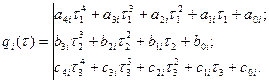 (i = 1,…,n)
(i = 1,…,n)
Используя условия 1, 2, 3 и 5, 9, найдем:
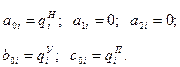 (i = 1,…,n)
(i = 1,…,n)
Продифференцируем сплайн-функции при условии, что 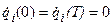 и
и 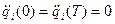
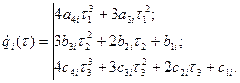
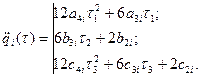
Запишем по оставшимся девяти граничным условиям систему девяти уравнений:
1) Условие 4: ( 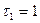 ):
): 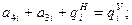
2) Условие 6: ( 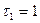 ;
; 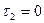 ):
): 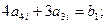
3) Условие 7: ( 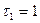 ;
; 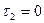 ):
): 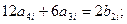
4) Условие 8: ( 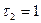 ):
): 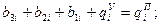
5) Условие 10: ( 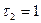 ;
; 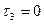 ):
): 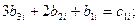
6) Условие 11: ( 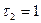 ;
; 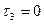 ):
): 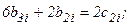
7) Условие 12: ( 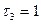 ):
): 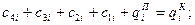
8) Условие 13: ( 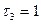 ):
): 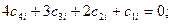
9) Условие 14: ( 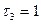 ):
): 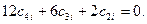
Решая эту систему девяти уравнений, определяются девять неизвестных коэффициентов.
Заметим, что такие системы уравнений должны быть записаны для каждой из n обощенных координат, следовательно, для робота с n степенями подвижности определению подлежит 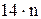 коэффициентов, при этом коэффициенты полиномов будут функциями параметров:
коэффициентов, при этом коэффициенты полиномов будут функциями параметров: 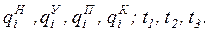
 Для еще большего уменьшения вероятности блуждания схвата используют сплайн-функции типа 3-3-3-3-3. В этом случае кроме ранее рассмотренных трех участков на участке АУАП вводятся две дополнительные опорные точки, и вместо этого одного участка возникает три (рис. 199).
Для еще большего уменьшения вероятности блуждания схвата используют сплайн-функции типа 3-3-3-3-3. В этом случае кроме ранее рассмотренных трех участков на участке АУАП вводятся две дополнительные опорные точки, и вместо этого одного участка возникает три (рис. 199).
Конкретные значения обобщенных координат в этих точках не регламентируются, что позволяет уменьшить число граничных условий (назначаются лишь моменты времени t2 и t3 (см. рис. 199) прохождения их схватом). В данном случае также будем пользоваться понятием относительного (нормированного) времени.
Запишем необходимые граничные условия для полиномов с учетом того, что сопряжение полиномов должно обеспечить на границах участков непрерывность скоростей и ускорений, а также выполнение ранее принятых условий прохождения схвата через точки АН, АУ, АП, АК.

|
1) 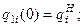
2) 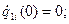
3) 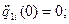
4) 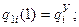
Участок 2:
5) 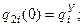
6) 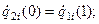
7) 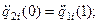
Таким образом, получено двадцать граничных условий, что равно числу коэффициентов пяти полиномов третьей степени.
Запишем сплайн-функцию 3-3-3-3-3.
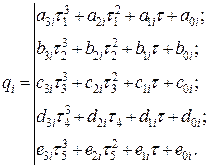
Из граничных условий 1, 2, 3, 5 и 15 определим коэффициенты: 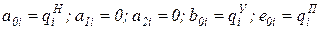 . Аналитические выражения для расчета остальных коэффициентов находятся из систем пятнадцати уравнений, составленных для каждой из n степеней подвижности манипулятора.
. Аналитические выражения для расчета остальных коэффициентов находятся из систем пятнадцати уравнений, составленных для каждой из n степеней подвижности манипулятора.
Общие случаи планирования траекторий в пространстве обобщенных координат
В тех случаях, когда точки АУ и АП удалены друг от друга на значительные расстояния может потребоваться большее число участков, чем три или пять. Увеличение числа участков может быть оправдано и в случае, если желательно обеспечить максимальную точность реализации траектории.
Возможны два варианта общих случаев:
Первый – когда координаты дополнительных точек не регламентированы как при рассмотрении 3-3-3-3-3 – траектории.
Второй (наиболее общий случай) – заданы координаты всех промежуточных точек.
Первый случай во многом аналогичен проектированию 3-3-3-3-3 – траектории. Рассмотрим этот случай при условии, что траектория разделена на m участков.
Учитывая, что 1-й и (m-1)-й участки должны иметь по четыре ограничения, m-й – шесть ограничений, а все промежуточные по три ограничения, можно записать выражение для расчета суммы Pm степеней полиномов, удовлетворяющих сформулированным условиям:
Pm= 4+4+6+3(m-3)-Pc = 5 + 2m , (m ≥ 3)
где Pc = m – сумма свободных членов полиномов.
В качестве примера использования полученной формулы рассчитаем сумму степеней ранее рассмотренных полиномов для случаев деления траектории соответственно на три и на пять участков:
 m = 3; Pm = 5+2·3 = 11; m = 5; Pm = 5+2·5 = 15.
m = 3; Pm = 5+2·3 = 11; m = 5; Pm = 5+2·5 = 15.
При m = 10;
Pm = 5+2·10 = 25.
Второй случай, как отмечалось, является наиболее общим случаем. Он возникает, когда траектория движения схвата является функцией времени и задана на всем протяжении в декартовых координатах О0x0y0z0 манипулятора (рис. 200).
В результате решения обратной задачи кинематики находятся соответствующие заданным точкам l (l = 0,…,m) значения обобщенных координат по каждой степени подвижности:
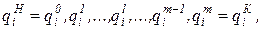
где m – число участков на траектории.
Запишем ограничения для рассматриваемого общего случая с использованием понятия относительного времени:
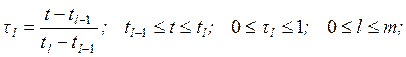
участок 1: 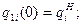
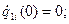
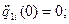
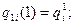
участок 2: 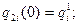
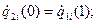

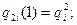
участок 3: 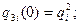
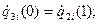
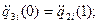
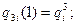
…………………………………………………………………
участок (l-1): 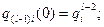
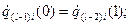

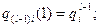
участок l: 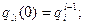
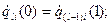
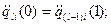
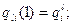
…………………………………………………………………
участок m: 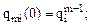

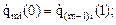
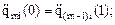
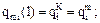
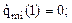
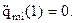
Определим необходимую сумму степеней аппроксимирующих полиномов, учитывая, что на участке m имеется шесть граничных условий, а на остальных по четыре.
Pm= 6+4(m-1)-Pc=2+3m, (m ≥ 3).
Общим недостатком такого представления сплайн-функций 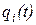 является необходимость предварительного решения систем большого числа уравнений для определения коэффициентов полиномов. Трудности усугубляются еще и тем, что при изменении числа участков появляется новая система уравнений, которую нужно решать заново.
является необходимость предварительного решения систем большого числа уравнений для определения коэффициентов полиномов. Трудности усугубляются еще и тем, что при изменении числа участков появляется новая система уравнений, которую нужно решать заново.
Законы движения 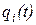 , полученные в ходе планирования обобщенной траектории, должны быть проверены на возможность исполнения их соответствующими приводами. Существуют ограничения на перемещения, скорости и ускорения.
, полученные в ходе планирования обобщенной траектории, должны быть проверены на возможность исполнения их соответствующими приводами. Существуют ограничения на перемещения, скорости и ускорения.
Ограничения на перемещения связаны с возможным диапазоном перемещения одного звена относительно другого. Для удовлетворения ограничений по перемещению следует определить экстремумы функций 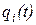 , что нетрудно выполнить после нахождения корней уравнения
, что нетрудно выполнить после нахождения корней уравнения 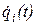 . Ограничения на обобщенные скорости
. Ограничения на обобщенные скорости 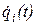 диктуются скоростными возможностями привода и допустимыми величинами накапливаемой кинетической энергии, а ограничения на обобщенные ускорения связаны с максимально возможными моментами и усилиями, которые могут развивать приводы.
диктуются скоростными возможностями привода и допустимыми величинами накапливаемой кинетической энергии, а ограничения на обобщенные ускорения связаны с максимально возможными моментами и усилиями, которые могут развивать приводы.
Траектория движения схвата и его ориентация могут быть заданы различным образом. В частности, она может быть задана, как отмечалось ранее, некоторым числом опорных точек.
Рассмотрим случай планирования траектории, когда она задана сравнительно небольшим числом опорных точек таким образом, что в основном траектория представляется отрезками прямых линий, сопряженными некоторыми переходными участками 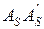 (рис. 201). Будем считать, что на каждом участке прямолинейного движения S схват перемещается с заранее заданными постоянными линейными скоростями
(рис. 201). Будем считать, что на каждом участке прямолинейного движения S схват перемещается с заранее заданными постоянными линейными скоростями 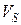 (см. рис. 201), т.е.
(см. рис. 201), т.е.
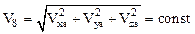
Координаты точек 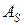 и
и 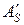 (S = 0,…,m) как обычно задаются вначале в декартовой системе, а затем известными методами решения обратной задачи находятся соответствующие значения обобщенных координат. Кроме того, назначаются координаты некоторого числа дополнительных точек на прямолинейных участках, достаточного для их реализации с заданной точностью.
(S = 0,…,m) как обычно задаются вначале в декартовой системе, а затем известными методами решения обратной задачи находятся соответствующие значения обобщенных координат. Кроме того, назначаются координаты некоторого числа дополнительных точек на прямолинейных участках, достаточного для их реализации с заданной точностью.
 Траектории переходных участков обычно не задаются строго. Эти участки предназначены для плавного изменения направления движения и для плавного перехода со скорости
Траектории переходных участков обычно не задаются строго. Эти участки предназначены для плавного изменения направления движения и для плавного перехода со скорости 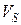 на скорость
на скорость 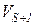 .
.
Здесь возможно два подхода:
· задание переходной траектории в пространстве декартовых координат, с последующим определением обобщенных координат, которые в этом случае могут оказаться напряженными для приводов.
· определение переходных участков в пространстве обобщенных координат (метод Пола). Этот подход дает более определенные результаты для управления приводами, но сама траектория на переходных участках может оказаться неприемлемой для движения схвата, например, из-за недопустимых инерционных перегрузок.
На рис. 202 представлен пример производственной сцены, в которой может возникнуть необходимость в прямолинейных движениях схвата.

Дата добавления: 2015-07-30; просмотров: 4445;

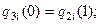 9)
9) 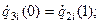 10)
10) 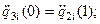 Участок 4:
11)
Участок 4:
11) 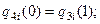 12)
12) 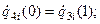 13)
13) 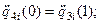 14)
14)