Основы кинематики манипуляционных систем
Приведем аналитические зависимости, связывающие перемещения звеньев манипулятора относительно друг друга при работе приводов с движением схвата в пространстве. Положение и ориентацию схвата в пространстве и времени задают законами движения центра схвата и углового движения последнего n-го звена, на котором закреплен схват, а именно:
xon = x(t), yon = y(t), zon = z(t);
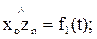
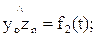 (t);
(t); 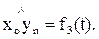
Положение i-го звена относительно (i-1)-го определяется с помощью обобщенной координаты qi.
Необходимо иметь математический аппарат, позволяющий устанавливать для манипулятора любой конфигурации математическую модель его кинематики, которую в общем виде можно представить следующим образом:
xon = x(q1, q2, ... qn; t),
yon = y(q1, q2, ... qn; t),
zon = z(q1, q2, ... qn; t),
xozn= f1(q1, q2, ... qn; t),
yozn = f2(q1, q2, ... qn; t),
xoyn = f3(q1, q2, ... qn; t),
или в более краткой форме записи
R = R (Q; t),
где R и Q – векторы абсолютных и обобщенных координат манипулятора.
Задачи подобного рода сводятся к преобразованию координат. В общем случае для того, чтобы зафиксировать одну систему координат относительно другой необходимо шесть координат: смещение по трем осям и поворот вокруг трех осей.
В связи с тем, что в манипуляторах роботов используются только одноподвижные вращательные и поступательные кинематические пары, для определения положения систем координат, связанных со звеньями манипулятора, достаточно четырех специальных координат. При этом сами системы координат должны быть связаны со звеньями манипулятора вполне определенным образом.
Специальные системы координат манипуляторов были предложены американскими учеными Д. Денавитом и Р. Хартенбергом в 1955–1960 гг. Первоначально они предназначались для задания осей кинематических пар пространственных рычажных механизмов с низшими парами (рис. 184).
В последние десятилетия предложенная координатная система была применена к описанию кинематики манипуляторов. Это связано с тем, что манипуляторы с одноподвижными вращательными и поступательными парами обладают рядом регулярных особенностей, хорошо согласующихся со свойствами координатной системы Денавита–Хартенберга.
 Cформулируем ряд правил расположения осей и начал координат специальной системы координат относительно кинематических пар и звеньев манипулятора. Пронумеруем кинематические звенья в последовательности от неподвижного звена к наиболее удаленному, на котором закреплен схват, присвоив им номера соответственно от 0 до n (рис. 185), где n – число подвижных звеньев манипулятора.
Cформулируем ряд правил расположения осей и начал координат специальной системы координат относительно кинематических пар и звеньев манипулятора. Пронумеруем кинематические звенья в последовательности от неподвижного звена к наиболее удаленному, на котором закреплен схват, присвоив им номера соответственно от 0 до n (рис. 185), где n – число подвижных звеньев манипулятора.
 Обозначим кинематические пары символом Ai, нижний индекс которого равен меньшему из номеров звеньев, образующих i-ю кинематическую пару (рис. 185). Например, кинематическая пара А1 соединяет кинематические звенья 1 и 2, а кинематическая пара А3 – кинематические звенья 3 и 4 и т.д. Обозначение Аn присваивается характерной точке (центру) схвата.
Обозначим кинематические пары символом Ai, нижний индекс которого равен меньшему из номеров звеньев, образующих i-ю кинематическую пару (рис. 185). Например, кинематическая пара А1 соединяет кинематические звенья 1 и 2, а кинематическая пара А3 – кинематические звенья 3 и 4 и т.д. Обозначение Аn присваивается характерной точке (центру) схвата.
Введем понятие оси zi i-й кинематической пары:
– осью zi i-й вращательной кинематической пары, соединяющей i-е звено с (i+1)-м является, ось шарнира кинематической пары Ai . Эту ось координат будем считать принадлежащей i-му звену и жестко с ним соединенной. Именно вокруг этой оси вращается (i+1)-е звено относительно i-го;
 – осью zi i-й поступательной пары является какая-либо из прямых, параллельная направляющей данной поступательной пары. По этой направляющей перемещается (i+1)-е звено относительно i-го. Если ось zi поступательной пары не параллельна оси zi-1, то ее рекомендуется направлять так, чтобы она пересекалась с этой осью.
– осью zi i-й поступательной пары является какая-либо из прямых, параллельная направляющей данной поступательной пары. По этой направляющей перемещается (i+1)-е звено относительно i-го. Если ось zi поступательной пары не параллельна оси zi-1, то ее рекомендуется направлять так, чтобы она пересекалась с этой осью.
За положительное направление оси zi можно взять любое, в частности, направления: снизу вверх, слева направо, по направлению к наблюдателю или близкие к ним направления.
Начало системы координат, связанной с i-м звеном, и направление оси xi выбирается по следующим правилам.
 Оси zi и zi-1 перекрещиваются: начало координат Oi располагается в точке пересечения линии кратчайшего расстояния между осями zi-1 и zi с осью zi (рис. 186). В этом случае ось xi направляется по линии кратчайшего расстояния в сторону от оси zi-1 к оси zi.
Оси zi и zi-1 перекрещиваются: начало координат Oi располагается в точке пересечения линии кратчайшего расстояния между осями zi-1 и zi с осью zi (рис. 186). В этом случае ось xi направляется по линии кратчайшего расстояния в сторону от оси zi-1 к оси zi.
Оси zi и zi-1 параллельны: за начало координат Оi может быть принята любая удобная по каким-либо соображениям точка оси координат zi (рис. 187). Ось xi направляется так, чтобы она лежала в плоскости, образуемой осями zi-1 и zi (случай рассматривается как частный по отношению к предыдущему).
Оси zi и zi-1 совпадают: начало Оi координат может быть назначено в любой удобной по каким-либо дополнительным условиям точке оси zi, а ось xi направлена перпендикулярно оси zi в произвольном направлении.
Оси zi и zi-1 пересекаются: за начало Oi координат принимается точка их пересечения, а ось xi направляется по общему перпендикуляру к осям zi и zi-1.
Эти правила не действуют в полной мере при выборе системы координат, связанной со стойкой (звено 0), т. к. отсутствует (i-1)-я кинематическая пара, и системы координат, связанной с последним n-м звеном, на котором закрепляется схват, т. к. это последнее звено не содержит кинематической пары, предназначенной для соединения с последующим звеном.
Начало О0 системы координат, связанной со стойкой (звеном 0), может быть расположено в любой точке оси z0, а направление оси xo принимается произвольно по дополнительным условиям (рис. 188, а).
 Начало Оn системы координат, связанной с последним n-м звеном манипулятора, на котором закреплен схват, располагается в точке, принимаемой за центр схвата, а ось xn направляется перпендикулярно оси zn-1 (рис.188, б). Направление оси zn может быть назначено произвольно, например, по оси захватываемой детали или технологического инструмента или перпендикулярно ей.
Начало Оn системы координат, связанной с последним n-м звеном манипулятора, на котором закреплен схват, располагается в точке, принимаемой за центр схвата, а ось xn направляется перпендикулярно оси zn-1 (рис.188, б). Направление оси zn может быть назначено произвольно, например, по оси захватываемой детали или технологического инструмента или перпендикулярно ей.
Во всех случаях ось OiYi напрявляется так, чтобы система координат была правой.
 При составлении математических моделей манипуляторов наибольшее распространение получило матричное исчисление. Долгое время для этой цели использовалось сочетание матриц поворота 3х3, элементами которых были направляющие косинусы углов между осями i-й и
При составлении математических моделей манипуляторов наибольшее распространение получило матричное исчисление. Долгое время для этой цели использовалось сочетание матриц поворота 3х3, элементами которых были направляющие косинусы углов между осями i-й и
(i-1)-й систем координат, и матриц переноса размером 3х1, элементами которых служили координаты начала i-й системы координат в (i-1)-й системе.
Наличие двух матриц разной размерности и разного назначения приводило к необходимости использования операций умножения и сложения матриц, к усложнению алгоритма вычислений, а, следовательно, к увеличению машинного времени, что сказывалось на отработке управляющих сигналов в реальном времени и на управляемости робота.
 В последнее время используются комплексные матрицы перехода размером 4х4, позволяющие осуществлять поворот и перенос (смещение) одних координат по отношению к другим. В этом случае для описания положения точки в пространстве применяются однородные координаты, в которых к обычным трем координатам добавляется четвертая, равная 1. Тогда координаты точки будут представлены в виде: xi,yi,zi,1.
В последнее время используются комплексные матрицы перехода размером 4х4, позволяющие осуществлять поворот и перенос (смещение) одних координат по отношению к другим. В этом случае для описания положения точки в пространстве применяются однородные координаты, в которых к обычным трем координатам добавляется четвертая, равная 1. Тогда координаты точки будут представлены в виде: xi,yi,zi,1.
Если известны однородные координаты xi,i, yi,i, zi,i, 1 вектора ri некоторой точки Аi в “старой” i-й системе координат, то однородные координаты xi-1,i, yi-1,i, zi-1,i, 1 вектора ri-1 этой точки в “новой” (i-1)-й системе координат рассчитываются в общем случае по формулам
(рис. 189):
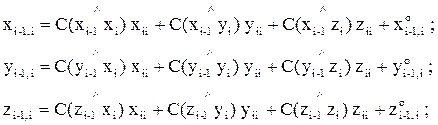 (1)
(1)
1 = 0 xii + 0 yii + 0 zii + 1 ,
где C – символ, обозначающий тригонометрическую функцию “cosinus”, 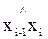 , . . . ,
, . . . , 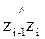 – углы, образуемые осями “старой” i-й системы координат с осями “новой” (i-1)-й системы так, что поворот определенной оси (i-1)-й системы до совмещения с соответствующей осью i-й системы виделся бы против часовой стрелки (рис. 190), x0i-1,i, y0i-1,i, z0i-1,i – координаты точки Oi в (i-1)-й системе координат.
– углы, образуемые осями “старой” i-й системы координат с осями “новой” (i-1)-й системы так, что поворот определенной оси (i-1)-й системы до совмещения с соответствующей осью i-й системы виделся бы против часовой стрелки (рис. 190), x0i-1,i, y0i-1,i, z0i-1,i – координаты точки Oi в (i-1)-й системе координат.
Тригонометрические функции 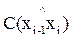 , . . . ,
, . . . , 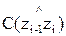 – называют направляющими косинусами осей i-й системы в (i-1)-й.
– называют направляющими косинусами осей i-й системы в (i-1)-й.
Выражение (1) можно переписать в матричном виде
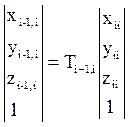 или Ri-1,i = Ti-1,i Ri,i , (2)
или Ri-1,i = Ti-1,i Ri,i , (2)
где
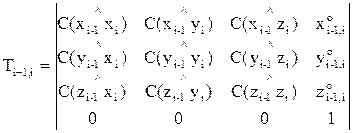 (3)
(3)
– однородная матрица перехода от системы i к (i-1)-й системе координат для (i-1)-й кинематической пары.
Матрицу Т i-1, i можно представить как блочную матрицу
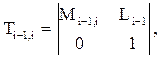
в которой матрица М i-1,i равная
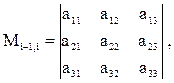
является матрицей поворота i-й системы координат относительно
(i-1)-й и содержит соответствующие направляющие косинусы.
Матрица L i-1, i является матрицей переноса начала координат i-й системы до совмещения с началом (i-1)-й,

где
Для сопоставления индексов выражения (1) и индексов матрицы М i-1, i, можно воспользоваться следующей таблицей:
| Первый индекс | Содержание 1-го индекса | Второй индекс | Содержание 2-го индекса |
| xi-1, | xi | ||
| yi-1 | yi | ||
| zi-1 | zi |
Переход от одной системы координат к другой с помощью матричного аппарата оказывается удобным средством описания кинематики манипулятора. Чтобы использовать матричный аппарат преобразования координат для описания кинематики манипуляторов, свяжем по изложенным ранее правилам с каждым i-м звеном манипулятора специальные системы координат, расположенные определенным образом в i-й кинематической паре.
В этом случае переход от i-й системы координат к (i-1)-й с помощью однородной матрицы перехода Т i-1, i можно трактовать как пересчет известных координат xii, yii, zii, точки Аi некоторого i-го звена в новую (i-1)-ю систему координат, связанную с (i-1)-м звеном. При переходе от i-й системы координат к (i-1)-й полагают, что оси i-й системы, “уходя” от (i-1)-й из положения, когда они полностью совпадали с (i-1)-й системой в то положение, которое они занимают, вращались против часовой стрелки относительно соответствующей оси поворота.
В общем случае, чтобы совместить “новое” (i-1)-е положение со “старым” i-м положением системы, используя движение “новой” системы к "старой", необходимо шесть независимых перемещений относительно трех осей координат.
Однако при использовании специальных систем координат и так называемых преобразований Денавита–Хартенберга достаточно четырех перемещений, осуществляемых в следующей последовательности (рис. 191):

1) Поворот (i-1)-й системы вокруг оси zi-1 против часовой стрелки на угол qi (если смотреть со стороны оси zi-1) до тех пор, пока ось xi-1 не станет параллельной и однонаправленной с осью xi;
2) Сдвиг повернутой (i-1)-й системы вдоль оси zi-1 на величину Si до тех пор, когда ось xi-1 совпадет с осью xi;
3) Сдвиг (i-1)-й системы вдоль оси xi на величину аi до совпадения начал координат систем (i-1) и i;
4) Поворот вокруг оси xi против часовой стрелки на угол ai (если смотреть со стороны оси xi) до совмещения оси zi-1 с осью zi.
Перечисленные эволюции (i-1)-й системы координат применительно к звеньям манипулятора показаны на рис. 191. Каждое из упомянутых элементарных движений (i-1)-й системы координат описывается соответствующей частной матрицей перехода.
1. Поворот вокруг оси zi-1 на угол qi:
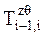 =
= 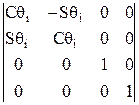 . (4)
. (4)
2. Сдвиг по оси zi-1 на величину Si:
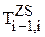 =
= 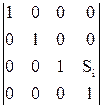 .
.
3. Сдвиг по оси xi на величину ai:
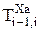 =
= 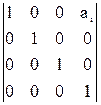 .
.
4. Поворот вокруг оси xi на угол ai:
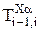 =
= 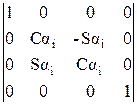 ,
,
где S означает тригонометрическую функцию “sinus”.
Результирующая матрица перехода от i-й системы координат к
(i-1)-й, т.е. матрица, осуществляющая преобразование системы
координат i-го звена в систему координат (i-1)-го звена, получается путем перемножения частных матриц перехода, а именно:
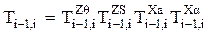 .
.
Параметры qi, Si, аi и ai могут принимать отрицательные значения.
После преобразований результирующая матрица перехода примет вид:
Тi-1, i= 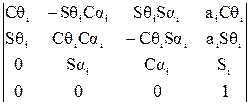 . (5)
. (5)
Матрица Тi-1,i является матрицей перехода 4х4 для (i-1)-й кинематической пары. Она позволяет найти по формуле (5) координаты
xi-1,i, yi-1,i, zi-1,i некоторой точки Аi в системе (i-1) по известным координатам xii, yii, zii этой точки в i-й системе координат и по известным параметрам qi, Si, аi и ai, кроме того, эта матрица дает возможность определить ориентацию i-го звена относительно (i-1)-го. Для этого обычно используются наддиагональные элементы а12, а13, а23 , a14, a24 и a34 матрицы Ti-1,i (см. зависимости (3) и (5)):

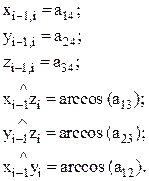
Продемонстрируем преобразование координат (рис. 192), применительно к частной матрице 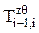 . В соответствии с зависимостью (1) можно записать
. В соответствии с зависимостью (1) можно записать
xi-1,iA = cosqi xi,iA + cos(90o+qi)yi,iA + cos 90ozi,iA + 0 ;
yi-1,iA = cos(270o+ qi)xi,iA + cosqi yi,iA + cos 90ozi,iA + 0 ;
zi-1,iA = cos 90oxi,iA + cos 90oyi,iA + cos 0ozi,iA + 0 ;
1=0oxi,iA+0oyi,iA+ 0ozi,iA+ 1
или, после преобразования по формулам приведения:
xi-1,iA = cosqi xi,iA - sinqi yi,iA + 0 zi,iA + 0 ;
yi-1,iA = sinqi xi,iA + cosqi yi,iA+ 0 zi,iA + 0 ;
zi-1,iA = 0oxi,i A +0oyi,iA+ 0ozi,iA + 0 ;
1 = 0oxi,iA +0oyi,iA +0ozi,iA + 1 .
Выписывая коэффициенты при 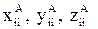 в отдельную матрицу, получим
в отдельную матрицу, получим
 =
= 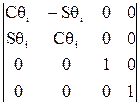 ,
,
аналогичную матрице (4), отражающей поворот i-й системы относительно оси zi-1 (i-1)-й системы на угол qi.
Приведем для справки матрицу поворота i-й системы вокруг оси yi-1 на угол bI:
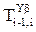 =
= 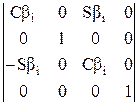 .
.
Дата добавления: 2015-07-30; просмотров: 1727;
