Уравнения высших порядков, допускающие понижение порядка
Уравнение n-го порядка 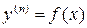 решается последовательным интегрированием.
решается последовательным интегрированием.
Умножая обе его части на 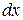 и интегрируя, получаем уравнение
и интегрируя, получаем уравнение 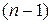 –го порядка:
–го порядка: 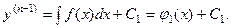
Снова умножая обе части на 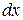 и интегрируя, получаем уравнение
и интегрируя, получаем уравнение 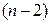 –го порядка:
–го порядка: 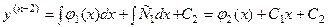 и т.д.
и т.д.
Пример 8.5.Решить дифференциальное уравнение 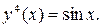
Решение.Проинтегрируем данное уравнение 4 раза:
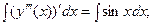
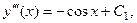
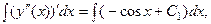
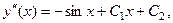

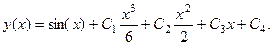
Решить дифференциальные уравнения:
8.1. 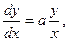 где
где  - постоянная
- постоянная 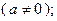 8.2.
8.2. 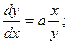
8.3. 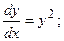 8.4.
8.4. 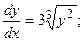
8.5. 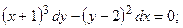 8.6.
8.6. 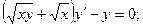
8.7. 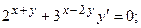 8.8.
8.8. 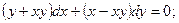
8.9. 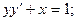 8.10.
8.10. 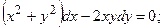
8.11. 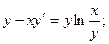 8.12.
8.12. 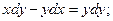
8.13. 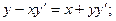 8.14.
8.14. 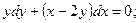
8.15. 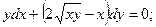 8.16.
8.16. 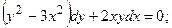
8.17. 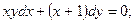 8.18.
8.18. 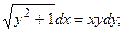
8.19. 
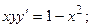 8.20.
8.20. 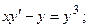
8.21. 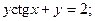 8.22.
8.22. 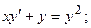
8.23. 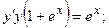 8.24.
8.24. 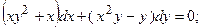
8.25. 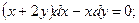 8.26.
8.26. 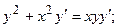
8.27. 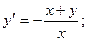 8.28.
8.28. 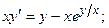
8.29. 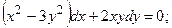 8.30.
8.30. 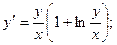
8.31. 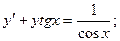 8.32.
8.32. 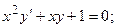
8.33. 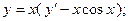 8.34.
8.34. 
8.35. 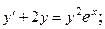 8.36.
8.36. 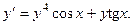
8.37. 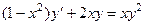 при условии
при условии 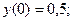
8.38. 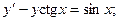 8.39.
8.39. 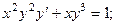
8.40. 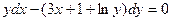 при условии
при условии 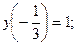
8.41. 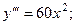 8.42.
8.42. 
8.43. 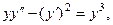 если
если 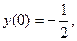
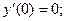
8.44. 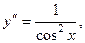 если
если 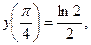
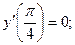
8.45. 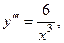 если
если 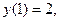
Варианты контрольных заданий
1. Вычислить предел функции:
| Вариант | Предел | Вариант | Предел |
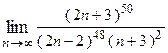
| 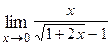
| ||
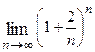
| 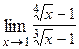
| ||
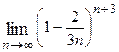
| 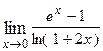
| ||
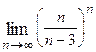
| 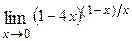
| ||
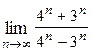
| 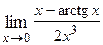
| ||
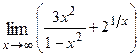
| 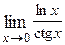
| ||
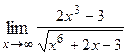
| 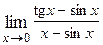
| ||

| 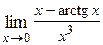
| ||
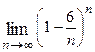
| 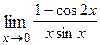
| ||
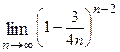
| 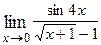
| ||
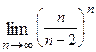
| 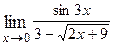
| ||
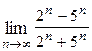
| 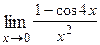
| ||

| 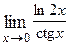
| ||
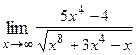
| 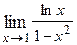
| ||
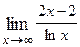
| 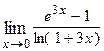
|
2. Исследовать функцию и построить её график:
| Вариант | Функция | Вариант | Функция |
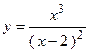
| 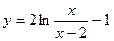
| ||
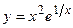
| 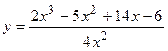
| ||
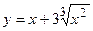
| 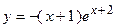
| ||
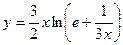
| 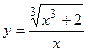
| ||
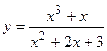
| 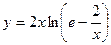
| ||
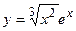
| 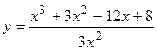
| ||
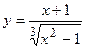
| 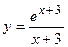
| ||
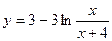
| 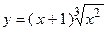
| ||
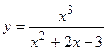
| 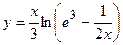
| ||
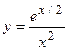
| 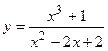
| ||
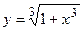
| 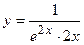
| ||
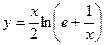
| 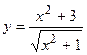
| ||
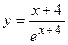
| 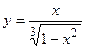
| ||
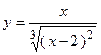
| 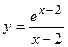
|
3. Найти неопределенный интеграл:
| Вариант | Интеграл | Вариант | Интеграл |
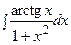
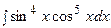
| 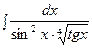
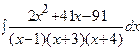
| ||
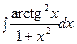
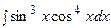
| 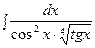
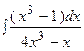
| ||
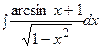
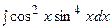
| 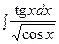
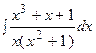
| ||
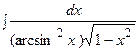
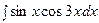
| 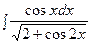
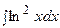
| ||
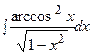
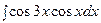
| 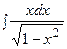
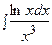
| ||
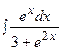
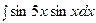
| 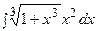
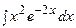
| ||
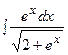
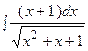
| 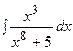
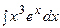
| ||
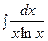
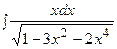
| 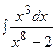
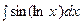
| ||

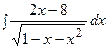
| 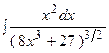 
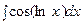
| ||
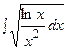
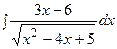
| 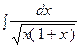
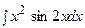
| ||
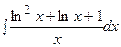
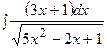
| 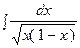
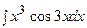
| ||
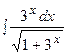
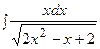
| 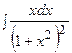
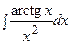
| ||
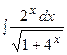
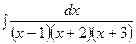
| 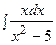
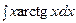
| ||
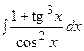
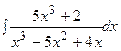
| 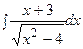
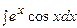
| ||
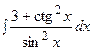
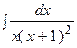
| 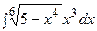
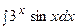
|
4. Вычислить площадь фигуры, ограниченной линиями:
| Вариант | Уравнения линий | Вариант | Уравнения линий |
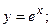 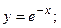 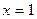
| 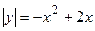
| ||
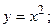 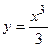
| 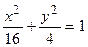
| ||
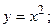 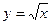
| 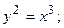 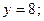 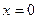
| ||
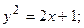 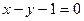
| 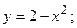 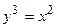
| ||
 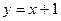
| 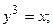 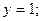 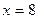
| ||
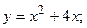 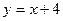
| 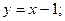 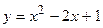
| ||
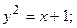 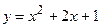
| 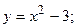 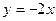
| ||
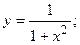 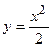
| 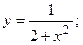 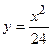
| ||
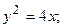 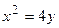
| 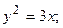 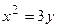
| ||
 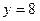
| 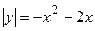
| ||
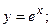 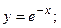 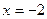
| 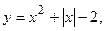 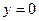
| ||
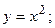 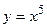
| 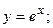 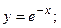 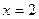
| ||
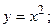 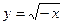
| 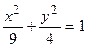
| ||
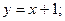 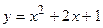
| 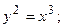 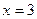
| ||
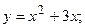 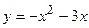
| 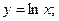 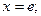 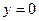
|
5. Исследовать сходимость ряда:
| Вариант | Ряд | Вариант | Ряд |
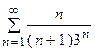
| 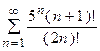
| ||
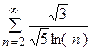
| 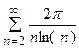
| ||
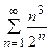
| 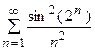
| ||
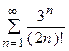
| 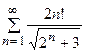
| ||
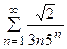
| 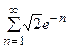 
| ||
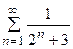
| 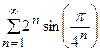
| ||
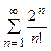
| 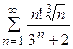
| ||
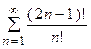
| 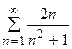
| ||
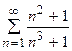
| 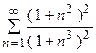
| ||
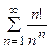
| 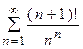
| ||
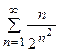
| 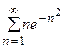
| ||
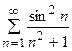
| 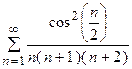
| ||
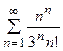
| 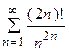
| ||
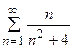
| 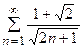
| ||
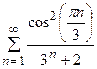
| 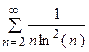
|
6. Решить дифференциальное уравнение первого порядка:
| Вариант | Уравнение | Вариант | Уравнение |
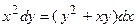
| 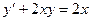
| ||

| 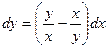
| ||
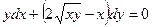
| 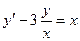
| ||
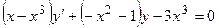
| 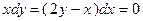
| ||
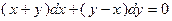
| 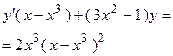
| ||
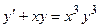
| 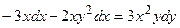
| ||
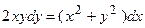
| 
| ||
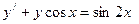
| 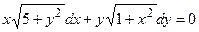
| ||
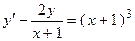
| 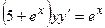
| ||
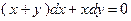
| 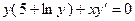
| ||
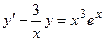
| 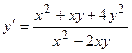
| ||
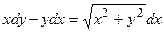
| 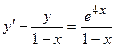
| ||
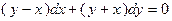
| 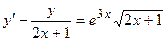
| ||
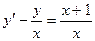
| 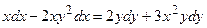
| ||

| 
|
Ответы
1.1. 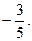 1.2.
1.2. 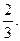 1.3.
1.3. 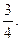 1.4.
1.4. 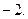 1.5.
1.5. 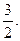 1.6.
1.6. 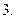 1.7.
1.7. 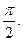 1.8.
1.8. 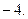 1.9.
1.9. 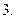 1.10.
1.10. 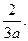 1.11. 0. 1.12.
1.11. 0. 1.12. 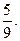 1.13.
1.13. 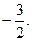 1. 14. -
1. 14. - 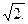 1.15. -2. 1.16. 2. 1.17. 4. 1.18.2. 1.19. 2. 1.20. 2
1.15. -2. 1.16. 2. 1.17. 4. 1.18.2. 1.19. 2. 1.20. 2  . 1.21.
. 1.21. 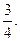 1.22.
1.22. 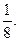 1.23. 3. 1.24. 1. 1.25. -1. 1.26. -49. 1.27. 2. 1.28. 0. 1.29. 2. 1.30. -
1.23. 3. 1.24. 1. 1.25. -1. 1.26. -49. 1.27. 2. 1.28. 0. 1.29. 2. 1.30. - 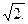 1.31. 0,1. 1.32. 1. 1.33. 1. 1.34. 0,5. 1.35. 2. 1.36.
1.31. 0,1. 1.32. 1. 1.33. 1. 1.34. 0,5. 1.35. 2. 1.36. 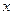 . 1.37.1. 1.38.
. 1.37.1. 1.38. 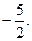 1.39.
1.39. 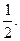 1.40.
1.40. 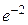 . 1.41.
. 1.41. 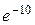 . 1.42.
. 1.42. 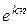 . 1.43.
. 1.43. 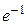 . 1.44.
. 1.44. 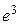 . 1.45. 9. 1.46.
. 1.45. 9. 1.46. 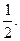 1.47. 1. 1.48.
1.47. 1. 1.48. 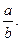 1.49.
1.49. 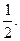 1.50.
1.50. 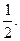 1.51. 0. 1.52.
1.51. 0. 1.52. 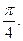 1.53.
1.53.  1.54.
1.54. 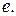 1.55. 0. 1.56.
1.55. 0. 1.56.  1.57.
1.57. 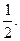 1.58.
1.58. 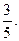 1.59.
1.59. 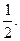 1.60.
1.60. 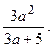 1.61. 0. 1.62. 1. 1.63.
1.61. 0. 1.62. 1. 1.63. 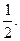 1.64. x. 1.65.
1.64. x. 1.65. 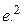 1.66.
1.66. 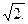 1.67.
1.67. 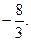 1.68.
1.68. 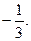 1.69. 3. 1.70.
1.69. 3. 1.70. 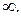 1.71. 0. 1.72.
1.71. 0. 1.72. 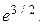 1.73.
1.73. 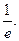 1.74. 0. 1.75.
1.74. 0. 1.75. 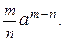 1.76. 2. 1.77.
1.76. 2. 1.77. 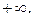 1.78. 1. 1.79. 1. 1.80.
1.78. 1. 1.79. 1. 1.80. 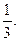 1.81. -3. 1.82.
1.81. -3. 1.82. 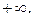 1.83.
1.83. 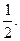 1.84.
1.84. 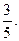 1.85. -1. 1.86. 1. 1.87.
1.85. -1. 1.86. 1. 1.87. 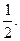 1.88. 0. 1. 89. -
1.88. 0. 1. 89. - 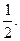 1.90. 0.
1.90. 0.
2.1. 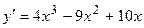 . 2.2.
. 2.2. 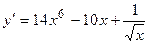 . 2.3.
. 2.3. 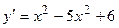 . 2.4.
. 2.4. 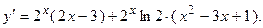 2.5.
2.5. 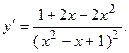 2.6.
2.6. 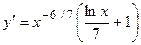 . 2.7.
. 2.7. 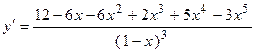 . 2.8.
. 2.8. 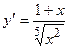 . 2.9.
. 2.9. 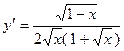 . 2.10.
. 2.10. 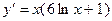 . 2.11.
. 2.11. 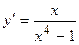 . 2.12.
. 2.12. 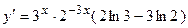 . 2.13.
. 2.13. 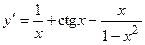 . 2.14.
. 2.14. 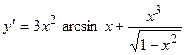 . 2.15.
. 2.15. 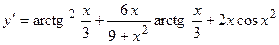 . 2.16.
. 2.16. 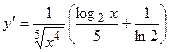 . 2.17.
. 2.17. 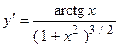 . 2.18.
. 2.18. 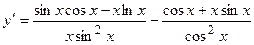 . 2.19.
. 2.19. 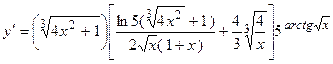 . 2.20.
. 2.20. 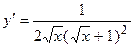 . 2.21.
. 2.21. 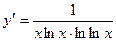 . 2.22.
. 2.22. 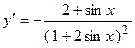 . 2.23.
. 2.23. 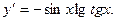 2.24.
2.24. 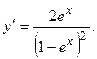 2.25.
2.25. 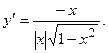 2.26.
2.26. 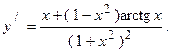 2.27.
2.27. 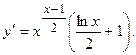 2.28.
2.28. 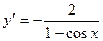 . 2.29.
. 2.29. 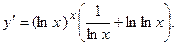 2.30.
2.30. 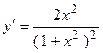 . 2.31.
. 2.31. 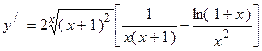 . 2.32.
. 2.32. 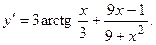 2.33.
2.33. 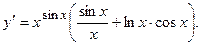 2.34.
2.34. 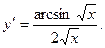 2.35.
2.35. 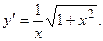 2.36.
2.36. 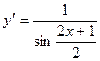 . 2.37.
. 2.37. 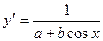 . 2.38.
. 2.38. 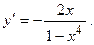 2.39.
2.39. 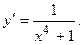 2.40.
2.40. 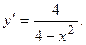 2.41.
2.41. 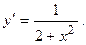 2.42.
2.42. 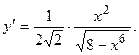 2.43.
2.43. 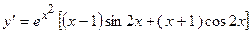 . 2.44.
. 2.44. 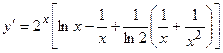 . 2.45.
. 2.45. 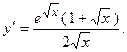 2.46.
2.46. 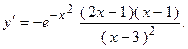 2.47.
2.47. 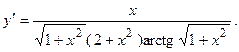 2.48.
2.48. 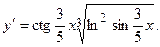 2.49.
2.49. 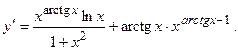
2.50.  .
.
2.51. 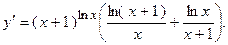 2.52.
2.52. 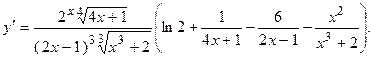
2.53. 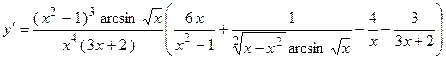 .
.
2.54. 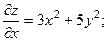
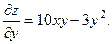 2.55.
2.55. 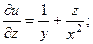
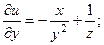
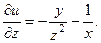
2.56. 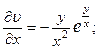
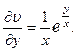 2.57.
2.57. 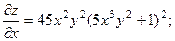
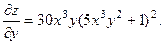
2.58. 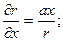
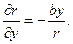 2.59.
2.59. 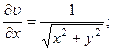
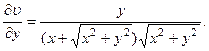 2.60.
2.60. 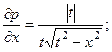
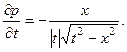
2.61. 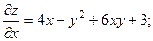
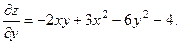
2.62. 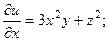
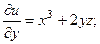
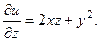
2.63. 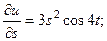
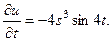 2.64.
2.64. 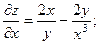
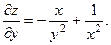
2.65. 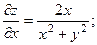
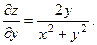 2.66.
2.66. 
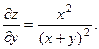
2.67. 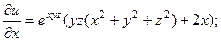
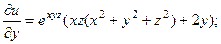
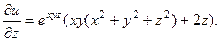 2.68.
2.68. 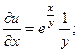
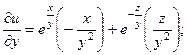
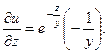 2.69.
2.69. 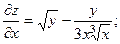
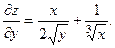 2.70.
2.70. 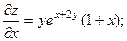
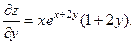 2.71.
2.71. 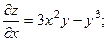
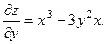 2.72.
2.72. 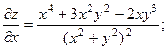
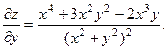 2.73.
2.73. 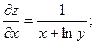
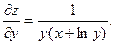
2.74. 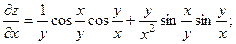
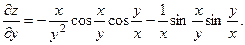
2.75. 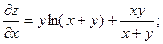
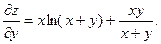 2.76.
2.76. 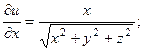
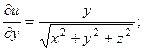
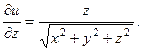 2.77.
2.77. 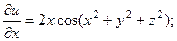
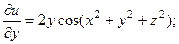
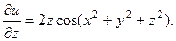 2.78.
2.78. 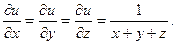 2.79.
2.79. 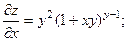
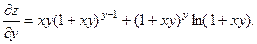 2.86.
2.86. 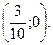 2.87.
2.87. 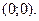 2.88.
2.88. 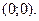 2.89.
2.89. 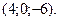 2.90.
2.90.  2.91.
2.91. 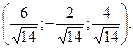 2.92.
2.92. 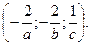 2.93.
2.93. 
3.1. Максимум в точке 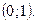
3.2. Минимум в точке  ; максимум в точке
; максимум в точке 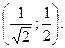
3.3. Максимум в точке 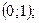 минимум в точке
минимум в точке 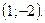
3.4. Максимум в точке 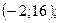 минимум в точке
минимум в точке 
3.5.Функция монотонно возрастает в интервале 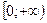 .
.
3.6.Точки экстремума 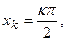
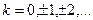 При четном
При четном 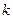 точки
точки 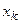 являются точками минимума, где
являются точками минимума, где 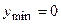 ; при нечетном
; при нечетном 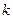 точки
точки 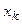 являются точками максимума, где
являются точками максимума, где 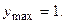
3.7. 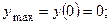
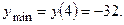
3.8. 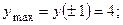
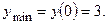
3.9.Экстремумов нет.
3.10. 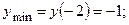
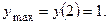
3.11. 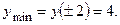
3.12. 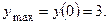
3.13.Максимум в точке 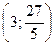 ; функция имеет перегиб в точках
; функция имеет перегиб в точках 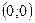 и
и 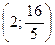 .
.
3.14. Минимум в точке 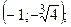 максимум в точке
максимум в точке 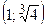 . В точке
. В точке 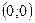 функция имеет перегиб.
функция имеет перегиб.
3.15. В точке 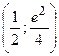 функция имеет минимум. В точке
функция имеет минимум. В точке 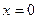 функция имеет разрыв II рода.
функция имеет разрыв II рода.
3.16. Функция определена и непрерывна на всей числовой оси. График пересекает оси координат в точках 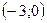 и
и 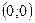 . Асимптот нет.
. Асимптот нет. 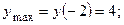
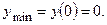 Точка перегиба
Точка перегиба 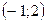 .
.
3.17. Функция определена и непрерывна на всей числовой оси. График пересекает оси координат в точках 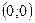 и
и 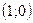 . Асимптот нет.
. Асимптот нет. 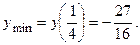 Точки перегиба
Точки перегиба 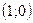 и
и 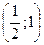 .
.
3.18.  – точки разрыва II рода. График пересекается с осями в начале координат. Асимптоты
– точки разрыва II рода. График пересекается с осями в начале координат. Асимптоты 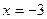 и
и 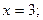
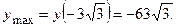
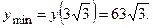 Точка перегиба
Точка перегиба 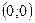 .
.
3.19. 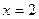 – точка разрыва II рода. График пересекает оси координат в точках
– точка разрыва II рода. График пересекает оси координат в точках 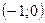 и
и 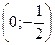 . Асимптоты
. Асимптоты 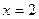 и
и 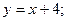
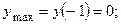
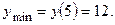 Точек перегиба нет (гипербола).
Точек перегиба нет (гипербола).
3.20. Функция определена и непрерывна всюду. График пересекается с осями в начале координат. Асимптота 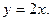 Экстремумов нет, функция всюду возрастает. Точки перегиба
Экстремумов нет, функция всюду возрастает. Точки перегиба 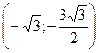 ,
, 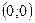 ,
, 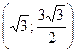 .
.
3.21. Функция определена и непрерывна всюду. График пересекает оси координат в точках 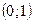 и
и 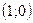 . Асимптота
. Асимптота 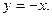 Экстремумов нет, функция всюду убывает. Точки перегиба
Экстремумов нет, функция всюду убывает. Точки перегиба 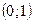 и
и 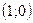 .
.
3.22. Область определения 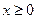 . График пересекает оси координат в точках
. График пересекает оси координат в точках 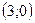 и
и 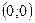 – концевая точка. Асимптот нет.
– концевая точка. Асимптот нет. 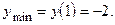 Точек перегиба нет.
Точек перегиба нет.
3.23. Минимум при 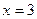 .
.
3.24. Максимум при 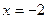 ; минимум при
; минимум при 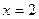 .
.
3.25. Максимум при 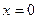 ; минимум при
; минимум при 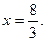
3.26. Функция имеет минимум в точке 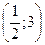 . В точке
. В точке 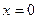 – имеет место разрыв II рода.
– имеет место разрыв II рода.
3.27. Максимум 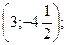 минимум
минимум 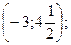 в точке
в точке 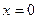 – перегиб; в точках
– перегиб; в точках 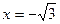 и
и 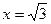 функция имеет разрывы II рода.
функция имеет разрывы II рода.
3.28. В точке 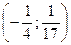 – минимум. В точке
– минимум. В точке 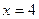 функция имеет разрыв II рода.
функция имеет разрыв II рода.
3.29. 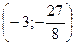 – максимум; в точке
– максимум; в точке 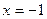 функция имеет разрыв II рода; в точке
функция имеет разрыв II рода; в точке 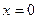 функция имеет перегиб.
функция имеет перегиб.
3.30. Минимум 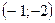 ; максимум
; максимум 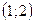 ;
; 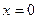 – точка перегиба.
– точка перегиба.
3.31. В точках  разрывы II рода; максимум в точке
разрывы II рода; максимум в точке 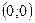 ;
; 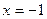 и
и 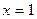 – вертикальные асимптоты;
– вертикальные асимптоты;  – горизонтальная асимптота.
– горизонтальная асимптота.
3.32. 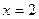 – точка разрыва II рода;
– точка разрыва II рода; 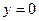 – горизонтальная асимптота;
– горизонтальная асимптота;  – максимум;
– максимум; 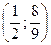 – точка перегиба.
– точка перегиба.
3.33. 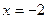 и
и 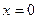 – точки разрыва II рода; вертикальные асимптоты:
– точки разрыва II рода; вертикальные асимптоты: 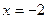 ,
, 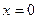 ; горизонтальная асимптота
; горизонтальная асимптота  ;
; 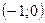 – максимум.
– максимум.
3.34. 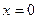 – точка разрыва II рода;
– точка разрыва II рода; 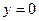 – горизонтальная асимптота;
– горизонтальная асимптота; 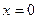 – вертикальная асимптота;
– вертикальная асимптота; 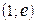 – точка минимума.
– точка минимума.
3.35. 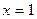 – точка разрыва II рода;
– точка разрыва II рода; 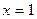 – вертикальная асимптота;
– вертикальная асимптота; 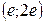 – точка минимума;
– точка минимума; 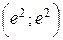 – точка перегиба.
– точка перегиба.
3.36. 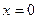 – вертикальная асимптота;
– вертикальная асимптота; 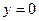 – горизонтальная асимптота;
– горизонтальная асимптота; 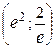 – максимум;
– максимум; 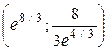 – точка перегиба.
– точка перегиба.
3.37. х=0 – вертикальная асимптота; y=x- наклонная асимптота; ( 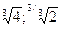 ) – минимум.
) – минимум.
3.38. 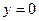 – горизонтальная асимптота;
– горизонтальная асимптота; 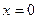 ,
, 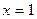 – вертикальные асимптоты;
– вертикальные асимптоты; 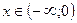 - функция выпукла вверх;
- функция выпукла вверх; 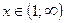 – функция выпукла вниз.
– функция выпукла вниз.
3.39. 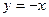 – наклонная асимптота;
– наклонная асимптота; 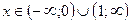 – функция выпукла вниз;
– функция выпукла вниз; 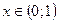 – функция выпукла вверх;
– функция выпукла вверх; 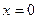 и
и 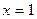 – точки перегиба.
– точки перегиба.
3.40. 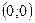 – точка максимума;
– точка максимума; 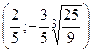 – точка минимума;
– точка минимума; 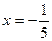 – точка перегиба.
– точка перегиба.
4.1. Дата добавления: 2015-07-30; просмотров: 899; 4.2.
4.2.  4.3.
4.3. 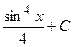 . 4.4.
. 4.4. 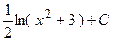 . 4.5.
. 4.5. 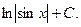 4
4
