Интегральный признак Коши
Пусть члены ряда 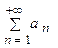 положительны и убывают, т.е.
положительны и убывают, т.е. 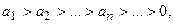 и пусть
и пусть 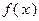 - непрерывная положительная убывающая функция, определенная при
- непрерывная положительная убывающая функция, определенная при 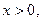 такая, что
такая, что
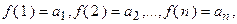 тогда интеграл
тогда интеграл 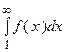 и ряд
и ряд 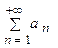 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Пример 7.1. Исследовать по признаку Даламбера сходимость ряда
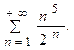
Решение. Зная, 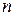 -й член ряда, находим следующий за ним (
-й член ряда, находим следующий за ним ( 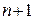 )-й член, заменяя в выражении
)-й член, заменяя в выражении 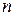 -го члена
-го члена 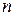 через (
через ( 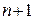 ). Затем ищем предел отношения последующего члена
). Затем ищем предел отношения последующего члена  к предыдущему
к предыдущему 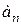 при неограниченном возрастании
при неограниченном возрастании 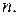
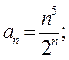
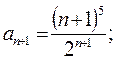
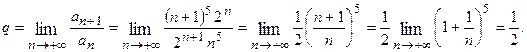
Здесь, 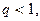 следовательно, согласно признаку Даламбера данный ряд сходится.
следовательно, согласно признаку Даламбера данный ряд сходится.
Пример 7.2. Исследовать по признаку Коши сходимость ряда 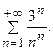
Решение. 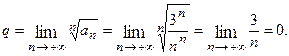
Здесь 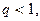 следовательно, согласно признаку Коши данный ряд сходится.
следовательно, согласно признаку Коши данный ряд сходится.
Пример 7.3. Исследовать по признаку сравнения сходимость ряда:
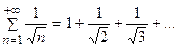
Решение.Сравним данный ряд с гармоническим рядом:
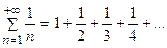
Каждый член 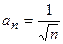 данного ряда, начиная со второго, больше соответствующего члена
данного ряда, начиная со второго, больше соответствующего члена 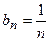 гармонического ряда:
гармонического ряда: 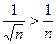 и, так как гармонический ряд расходится, то, согласно признаку сравнения, данный ряд также расходится.
и, так как гармонический ряд расходится, то, согласно признаку сравнения, данный ряд также расходится.
Пример 7.4. Исследовать по признаку сравнения сходимость ряда:
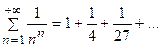
Решение. Сравним данный ряд с бесконечной геометрической прогрессией:  , которая представляет сходящийся ряд. Каждый член исследуемого ряда
, которая представляет сходящийся ряд. Каждый член исследуемого ряда 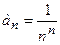 , начиная с третьего, меньше соответствующего члена
, начиная с третьего, меньше соответствующего члена 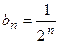 бесконечной геометрической прогрессии:
бесконечной геометрической прогрессии:
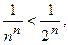 следовательно, согласно признаку сравнения, исследуемый ряд является сходящимся.
следовательно, согласно признаку сравнения, исследуемый ряд является сходящимся.
Пример 7.5.Исследовать по интегральному признаку сходимость ряда:
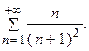
Решение. Заменяем в заданном выражении общего члена ряда 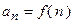 номер
номер 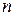 непрерывной переменной
непрерывной переменной 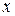 и убеждаемся, что полученная функция
и убеждаемся, что полученная функция 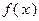 является непрерывной и убывающей во всем бесконечном интервале изменения
является непрерывной и убывающей во всем бесконечном интервале изменения 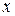 . Затем находим несобственный интеграл от
. Затем находим несобственный интеграл от 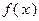 с бесконечным верхним пределом.
с бесконечным верхним пределом.
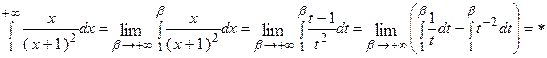

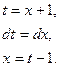
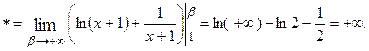
Здесь несобственный интеграл расходится. Следовательно, согласно интегральному признаку, и данный ряд также расходится.
Исследовать на сходимость следующие ряды:
7.1. 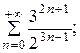 7.2.
7.2. 
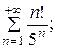
7.3. 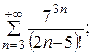 7.4.
7.4. 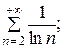
7.5. 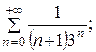 7.6.
7.6. 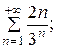
7.7. 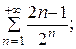 7.8.
7.8. 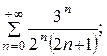
7.9. 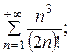 7.10.
7.10. 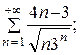
7.11. 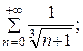 7.12.
7.12. 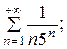
7.13. 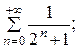 7.14.
7.14. 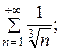
7.15. 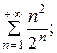 7.16.
7.16. 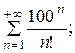
7.17. 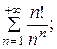 7.18.
7.18. 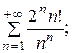
7.19.  7.20.
7.20. 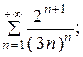
7.21. 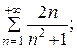 7.22.
7.22. 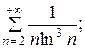
7.23. 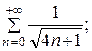 7.24.
7.24. 
Дата добавления: 2015-07-30; просмотров: 1247;
