Однородные дифференциальные уравнения первого порядка
Дифференциальное уравнение вида:
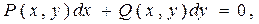
где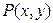 
и 
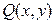– однородные функции одинакового измерения, называется однородным дифференциальным уравнением первого порядка. Данное уравнение можно привести к виду 
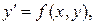где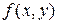 
– однородная функция нулевого измерения. С помощью замены 
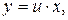где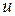 
– новая неизвестная функция, рассматриваемое уравнение сводится к уравнению с разделяющимися переменными.
Пример 8.2.Решить дифференциальное уравнение: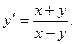 
Решение. Сделаем замену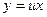 
и получим:
;
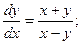
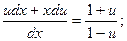
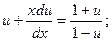
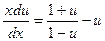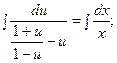
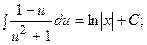
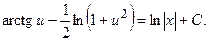
Сделав обратную замену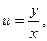 
получим общий интеграл:
Дата добавления: 2015-07-30; просмотров: 817;