Линейные дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид
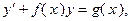
где 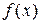 и
и 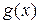 – некоторые (непрерывные) функции переменной
– некоторые (непрерывные) функции переменной 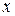 . В случае, когда функция
. В случае, когда функция 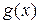 тождественно равна нулю, уравнение называется однородным, в противном случае – неоднородным.
тождественно равна нулю, уравнение называется однородным, в противном случае – неоднородным.
Будем искать решение в виде 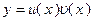 . Очевидно, что здесь искомыми становятся функции
. Очевидно, что здесь искомыми становятся функции 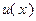 и
и 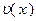 . Так как
. Так как 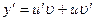 , то из определения следует
, то из определения следует 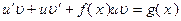 или
или 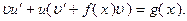
Найдем сначала какое-либо частное решение 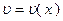 уравнения
уравнения
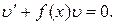
Тогда функция 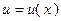 – решение уравнения
– решение уравнения
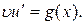
Таким образом, решение исходного уравнения сводится к решению двух уравнений с разделяющимися переменными.
Пример 8.3.Решить уравнение 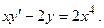
Решение.Разделив обе части уравнения на 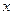 , получим линейное неоднородное уравнение:
, получим линейное неоднородное уравнение:
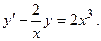
Пусть 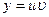 , т.е.
, т.е. 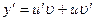 , тогда исходное уравнение примет вид
, тогда исходное уравнение примет вид 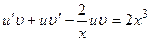 или
или
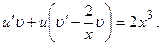
Положим 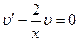 или
или 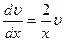 , откуда
, откуда 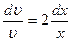 . Проинтегрировав, найдем какое-либо частное решение этого уравнения, например, при
. Проинтегрировав, найдем какое-либо частное решение этого уравнения, например, при 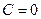
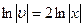 и
и 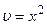 . При
. При 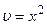 равенство
равенство 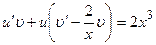 обратится в уравнение
обратится в уравнение 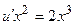 , или
, или 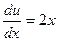 . Решая данное уравнение с разделяющимися переменными, получаем
. Решая данное уравнение с разделяющимися переменными, получаем 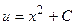 . Тогда окончательно имеем:
. Тогда окончательно имеем:
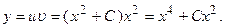
Дата добавления: 2015-07-30; просмотров: 749;
