Хімічний потенціал. Ферміони і бозони. Невироджені та вироджені системи частинок. Поняття про функцію розподілу

Будь-яке тверде тіло складається з великої кількості частинок. Такі системи вивчаються в розділах фізики: термодинаміка і статистична фізика. При цьому одним із важливих параметрів системи є хімічний потенціал μ. Згідно з першим началом термодинаміки змінити внутрішню енергію U системи можна трьома шляхами:

- за рахунок передачі системі певної кількості теплоти ΔQ;

- виконанням системою, чи над нею механічної роботи А=P×ΔV;

- зміною кількості частинок на ΔN.

Таким чином можемо записати

ΔU=ΔQ - P×ΔV + μ×ΔN, (2.1)

де μ – хімічний потенціал. При ΔQ=0 і ΔV=0 μ= ΔU/ ΔN. Тобто хімічний потенціал - це та частина внутрішньої енергії, яку вносить одна частинка в теплоізольовану систему незмінного об’єму.

Рівноважним станом системи є однакове значення хімічного потенціалу в будь-якій її точці. По характеру поводження частинок в системі вони поділяються на два типи: ферміони і бозони. Ферміони – це частинки з напівцілим спіном ( 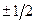). Це електрони, протони, нейтрони. Бозони – частинки з цілим спіном. Це фотони, фонони, піони та ін. Ферміонам властивий принцип Паулі, тобто в одному квантовому стані може знаходитись тільки один ферміон. Якщо квантовий стан зайнятий, то інша частинка з ферміонними властивостями в нього потрапити не може, поки він не звільниться. Тобто ферміони мають властивість „уособлення”. Бозони ж навпаки з більшою ймовірністю займають уже зайнятий квантовий стан. Принцип заборони Паулі їм не властивий. Тобто бозони мають „колективістські” властивості. Для того, щоб ферміонні чи бозонні властивості частинок проявились у системі, вони повинні взаємодіяти між собою, тобто зустрічатись. Критерієм К частоти зустрічі частинок є відношення кількості частинок N до кількості квантових станів G у системі. Якщо відношення , частота зустрічі частинок одна з одною дуже мала, і їхні ферміонні чи бозонні властивості не проявляються. У розпорядженні кожної частинки є велика кількість квантових станів. Тому питання про характер і послідовність їх заповнення неактуальне. Такі системи називаються невиродженими і описуються класичною статистикою Максвелла-Больцмана. 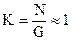При питання про заповнення квантових станів стає актуальним. Це вироджені системі і описуються функціями Фермі-Дірака (ферміони) і Бозе-Ейнштейна (бозони).

Введемо поняття функції розподілу та встановимо її фізичний зміст. Позначимо кількість квантових станів в інтервалі енергій від Е до Е+dЕ як g(E)×dE, де g(E) – густина квантових станів, тобто їх кількість в одиничному інтервалі енергій. Якщо позначити ймовірність заняття частинкою квантового стану з енергією Е як f(E), то кількість частинок в інтервалі енергій від Е до Е+dЕ буде дорівнювати

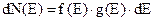(2.2)

і називається повною статистичною функцією розподілу по енергіям. Аналогічно вводяться функції розподілу по іншим фізичним величинам: за швидкостями, за імпульсами і т.д.