Густина квантових станів
Стан мікрочастинки характеризується трьома координатами x,y, z і трьома проекціями імпульсу px, py, pz. Такий шестимірний простір називається фазовим простором. Величина
dГ=dГv×dГр=dx×dy×dz×dpx×dpy×dpz (2.3)
називається елементом цього простору. Тут dГv= dx×dy×dz – елемент об’єму, dГр=dpx×dpy×dpz – елемент простору імпульсів.
Для класичної частинки ці величину можуть бути скільки завгодно малими, тому що фізичні величини змінюються неперервно. Для квантових же частинок, які мають хвильові властивості, фізичні величини змінюються дискретно. У відповідності з принципом невизначеності Гейзенберга dx×dpx≥h; dy×dpx≥h; dz×dpz ≥h, де h – стала Планка. Тому мінімальний об’єм фазового простору dГ=dГv×dГр= h3.
Для вільних квантових частинок, тобто коли на них не діє силове поле, важливими є їхня кінетична енергія, або імпульс, тому що вони можуть займати будь-яку точку геометричного простору. В цьому випадку зручніше користуватись не 6-мірним фазовим простором, а 3-мірним простором імпульсів, найменший елемент якого dГр= h3/V, де V – об’єм системи.

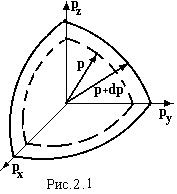 Поділ фазового простору на найменші елементи dГ, чи dГр називається його квантуванням. Знайдемо густину квантових станів спочатку у просторі імпульсів g(p), а потім перейдемо до енергій g(E). Для цього у просторі імпульсів виберемо сферу радіусом р, і порахуємо кількість елементів dГр в сферичному шарі товщиною dp. На рис.2.1 зображена ⅛ частина цього шару у першому квадранті. Кількість квантових станів g(p)×dp у цьму сферичному шарі дорівнює відношенню його об’єму 4πp2dp до мінімального об’єму елементу dГр. Маємо
Поділ фазового простору на найменші елементи dГ, чи dГр називається його квантуванням. Знайдемо густину квантових станів спочатку у просторі імпульсів g(p), а потім перейдемо до енергій g(E). Для цього у просторі імпульсів виберемо сферу радіусом р, і порахуємо кількість елементів dГр в сферичному шарі товщиною dp. На рис.2.1 зображена ⅛ частина цього шару у першому квадранті. Кількість квантових станів g(p)×dp у цьму сферичному шарі дорівнює відношенню його об’єму 4πp2dp до мінімального об’єму елементу dГр. Маємо
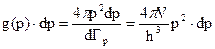 . (2.4)
. (2.4)
Тоді густина квантових станів 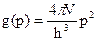 . (2.5) Знайдемо функцію g(E). Для цього в рівняння (2.4) підставимо імпульс
. (2.5) Знайдемо функцію g(E). Для цього в рівняння (2.4) підставимо імпульс 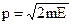 , і
, і 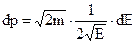 . Після спрощень одержимо
. Після спрощень одержимо
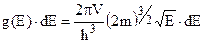 , звідки маємо для густини квантових станів по енергіям
, звідки маємо для густини квантових станів по енергіям
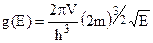 (2.6)
(2.6)
Графіки функцій (2.5) і (2.6) густини квантових станів:

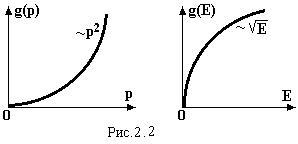 |
Із графіків видно, що з ростом р і Е густина g(p) і g(E) квантових станів зростає, а тому критерій частоти зіткнень частинок зменшується і може від значення близького до 1 зменшитись до значення набагато меншого за 1. А це означає, що система із виродженої може стати невиродженою, або кажуть виродження знімається.
Для електронів, враховуючи, що у кожному квантовому стані може знаходитись дві частинки з протилежними спінами, густина квантових станів у два рази більша, ніж за виразами (2.5) і (2.6).
Приклад. З’ясувати характер двох систем: 1) азот при нормальних умовах; 2) електронний газ в металах і напівпровідниках.
Оцінимо критерій К виродженості системи. Кількість частинок N=n×V, де n-концентрація, V- об’єм системи. Кількість квантових станів
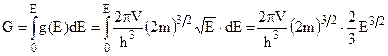 .
.
Враховуючи, що енергія частинки 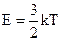 , після скорочень одержуємо
, після скорочень одержуємо 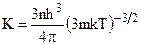 .
.
Для азоту маємо: n=2,7×1025 м-3–це число Лошмідта, m=28×1,66×10-27 кг, Т=273К, h=6,62×10-34 Дж×с, k=1,38×10-23 Дж/К. Розрахунок дає К≈10-6 <<1. Це набагато менше за 1. Отже азот – система не вироджена.
В металах концентрація порядку 5×1028 м-3, тобто приблизно у 1000 разів більша, маса електрона m=9×10-31 кг на 5 порядків менша. Це приводить до зростання К. Щоб значення критерію К було в межах 0,5-1, потрібна температура приблизно 105 К. А при таких температурах метали в твердій фазі не існують. Отже електронний газ в металах завжди вироджений і описується квантовою статистикою Фермі-Дірака. У напівпровідниках же концентрація електронів на 6 порядків менша, ніж у металах. Тому ця система навіть при кімнатній температурі невироджена і описується класичною статистикою Максвелла-Больцмана.
2.3 Функція розподілу для невироджених систем (функція Максвелла-Больцмана)
Функція Максвелла- Больцмана описує невироджені системи як ферміонів, так і бозонів, і має вид
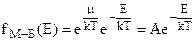 , (2.7)
, (2.7)
де μ – хімічний потенціал. Його можна знайти із умови нормування функції розподілу
 (2.8)
(2.8)
Інтеграл взятий заміною 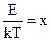 , враховуючи, що
, враховуючи, що 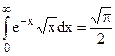 є табличним. Одержуємо нормовану функцію Максвелла-Больцмана
є табличним. Одержуємо нормовану функцію Максвелла-Больцмана
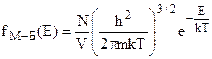 . (2.9)
. (2.9)
Із виразів (2.2), (2.6) і (2.9) після спрощень одержимо нормовану повну статистичну функцію розподілу Максвелла-Больцмана
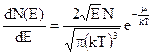 . (2.10)
. (2.10)
 Графіки функцій (2.7) і (2.10) мають вид
Графіки функцій (2.7) і (2.10) мають вид

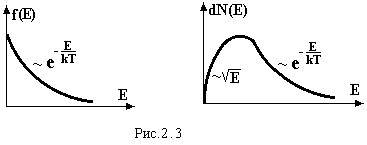 |
2.4 Функція розподілу для вироджених систем (функція Фермі-Дірака)
Функція Фермі-Дірака описує вироджені системи ферміонів і має вид
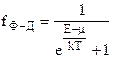 (2.11)
(2.11)
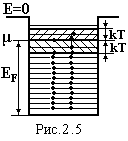


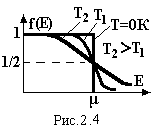 Графік цієї функції показаний на рис.2.4. При температурі Т=0К і Е<μ f(E)=1, а при E>μ f(E)=0. Це означає, що квантові стани, в яких енергія частинок менша від хімічно-го потенціалу μ, займаються з ймовірністю 1, тобто всі вони зайняті. Ймовірність же зайняття рівнів, енергія частинок на яких більша від хімічного потенціалу, дорівнює нулю, тобто вони всі вільні. Рівень, на якому енергія частинок дорівнює хімічному потенціалу, називається рівнем Фермі. При температурах, відмінних від абсолютного нуля при Е=μ f(E)=1/2. Отже рівень Фермі – це енергетичний рівень, ймовірність зайняття якого частинками дорівнює 1/2. При збільшенні температури край функції розподілу Фермі-Дірака розмивається. і чим вища температура, тим більше розмиття, яке охоплює інтервал енергій ±kT. Це означає, що частинки з енергією меншою, але близькою до рівня Фермі зазнають теплового збудження, тобто одержують теплову енергію, і переходять на більш високі енергетичні рівні за рівень Фермі. Метал, а саме в ньому електронний газ описується цією функцією, представляє для електронів потенціальну яму з дискретним енергетичним спектром, показаним на рис.2.5. З нього видно, що максимальну кінетичну енергію при Т=0К мають електрони, які знаходяться на рівні Фермі μ. Ця кінетична енергія, відрахована від дна ями (від найнижчого рівня) називається енергією Фермі EF. Знайдемо її із умови, що при Т=0К інтеграл
Графік цієї функції показаний на рис.2.4. При температурі Т=0К і Е<μ f(E)=1, а при E>μ f(E)=0. Це означає, що квантові стани, в яких енергія частинок менша від хімічно-го потенціалу μ, займаються з ймовірністю 1, тобто всі вони зайняті. Ймовірність же зайняття рівнів, енергія частинок на яких більша від хімічного потенціалу, дорівнює нулю, тобто вони всі вільні. Рівень, на якому енергія частинок дорівнює хімічному потенціалу, називається рівнем Фермі. При температурах, відмінних від абсолютного нуля при Е=μ f(E)=1/2. Отже рівень Фермі – це енергетичний рівень, ймовірність зайняття якого частинками дорівнює 1/2. При збільшенні температури край функції розподілу Фермі-Дірака розмивається. і чим вища температура, тим більше розмиття, яке охоплює інтервал енергій ±kT. Це означає, що частинки з енергією меншою, але близькою до рівня Фермі зазнають теплового збудження, тобто одержують теплову енергію, і переходять на більш високі енергетичні рівні за рівень Фермі. Метал, а саме в ньому електронний газ описується цією функцією, представляє для електронів потенціальну яму з дискретним енергетичним спектром, показаним на рис.2.5. З нього видно, що максимальну кінетичну енергію при Т=0К мають електрони, які знаходяться на рівні Фермі μ. Ця кінетична енергія, відрахована від дна ями (від найнижчого рівня) називається енергією Фермі EF. Знайдемо її із умови, що при Т=0К інтеграл 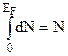 дорівнює загальній кількості частинок, а
дорівнює загальній кількості частинок, а 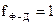 . Одержимо
. Одержимо 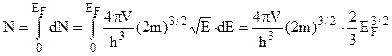 .
.
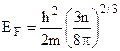 Отже,
Отже, 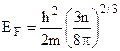 . (2.12)
. (2.12)
Тут n=N/V – концентрація електронів. При n=1028 м-3 ЕF ≈ 1,5 еВ. Зручніше задавати цю енергію характеристичною температурою Фермі TF, яка вводиться із рівняння EF = kTF. При оціненому значенні енергії Фермі температура Фермі дорівнює TF=2×104K, яка набагато більша від температури плавлення металів. Цей результат ще раз доводить, що електронний газ в металах завжди вироджений.
Оцінимо долю електронів, які при температурі Т зазнають теплового збудження, тобто знайдемо долю частинок, які знаходяться в інтервалі kT енергії поблизу рівня Фермі. Відстань між енергетичними рівнями в потенціальній ямі 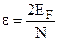 . Тоді кількість енергетичних рівнів в інтервалі kT буде
. Тоді кількість енергетичних рівнів в інтервалі kT буде 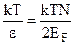 . Враховуючи, що електронів у 2 рази більше, ніж рівнів, але ймовірність іх заняття поблизу рівня Фермі майже 0,5, одержуємо
. Враховуючи, що електронів у 2 рази більше, ніж рівнів, але ймовірність іх заняття поблизу рівня Фермі майже 0,5, одержуємо
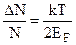 . (2.13)
. (2.13)
Навіть при температурі 1000К ця доля збуджених електронів не перевищує 1÷2%.
Як же змінюється функція Фермі-Дірака при високих температурах? Коли Е-μ >> kT, тобто Е >> μ + kT, одиницею в знаменнику функції (2.11) можна знехтувати, і функція перейде у функцію (2.7) Максвелла-Больцмана, як і повинно бути у випадку переходу виродженої системи в невироджену.
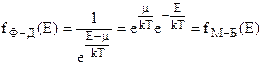 .
.
Дата добавления: 2015-07-24; просмотров: 1358;
