Реальные газовые системы. Летучесть

В предыдущих параграфах было показано, как, используя уравнение состояния идеального газа, была найдена зависимость химического потенциала вещества в идеальной смеси от содержания этого вещества (парциального давления или молярной доли).

Все идеальные газы подчиняются одному и тому же уравнению состояния. В отличие от них практически для каждого реального газа требуется свое уравнение состояния, отличающееся если не по форме, то входящими в него константами.

Например, в известном уравнении Ван-дер-Ваальса

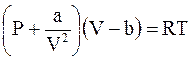
константа а может изменяться в несколько раз, а отношение ее значений для октана и гелия превышает 1000.

Если использовать отдельные уравнения для нахождения зависимости химического потенциала от содержания вещества в смеси, то пришлось бы для каждого вещества создавать свою термодинамику, что сделало бы необычайно сложным практическое применение результатов.

Развитие термодинамики пошло по другому пути, в разработке которого огромную роль сыграли работы Льюиса и Рэндалла. Было предложено сохранить форму термодинамических уравнений, полученных для идеальных газовых смесей, заменив давление функцией от давления. Поскольку зависимость химического потенциала от содержания вещества в смеси применима только к условию постоянной температуры, то и вновь вводимая функция должна быть изотермической, т.е. устанавливаться каждый раз при изменении температуры.

Функция, заменившая давление в термодинамических уравнениях для реальных газов, получила название летучести, или фугитивности. Ее обычно обозначают f.

Условия введения летучести таковы:

* при приближении состояния реального газа к свойствам идеального газа (это может происходить при понижении давления) летучесть приближается к давлению, что означает полное совпадение летучести и давления у идеальных газов;

* форма уравнений с летучестью полностью повторяет форму уравнений, выведенных для идеального газа.

Сравним эти формы друг с другом и общей формой термодинамических уравнений в изотермических условиях (см. табл. 6 - 1).

Таблица 6 - 1

Сравнение форм термодинамических

уравнений для газов

	Общая форма термодинамиче-ского уравнения	Форма уравнения для идеального газа	Форма уравнения для реального газа
Бесконечно малое (элементарное) приращение энергии Гиббса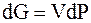
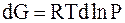
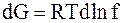
Конечное приращение энергии Гиббса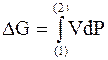

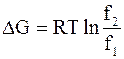
Приравнивая правые части уравнений в первом и последнем столбце последней строки, получим

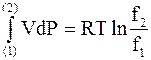(6 - 35)

или

. (6 - 36)

Уравнение (6 - 36) служит для нахождения отношения летучестей.

Обычно при заданной температуре находят зависимость объема газа от его давления и проводят интегрирование функции V=V(P) от давления Р₁ до давления Р₂. Интегрирование осуществляют или с применением эмпирического уравнения, отражающего зависимость объема от давления, или графическими методами на основе экспериментально полученного графика этой функции.

О проявляемом физико-химиками искусстве графического интегрирования можно судить по следующей истории.

Рассказывают, что выдающийся американский изобретатель Т.Эдисон в преклонном возрасте решил найти себе преемника. Был объявлен конкурс, в ходе которого Эдисон предложил молодым людям найти объем колбы электрической лампы. Молодые претенденты на звание преемника самого Эдисона предлагали разнообразные способы, включая проектирование колбы на большой экран, чтобы найти уравнение поверхности колбы для последующего интегрирования. К своему сожалению, Эдисон не нашел в числе предложенных ими ни одного простого и точного способа. После окончания конкурса он взвесил колбу, налил в нее воду и снова взвесил. Объем колбы был установлен с высокой точностью.

Мало кто из физико-химиков знает о конкурсе, устроенном Эдисоном. Однако методикой определения площади под кривой, т.е. графического интегрирования, владеют многие из них. Когда необходимо определить площадь под кривой, физико-химик проводит эту кривую на миллиметровой бумаге, а затем вырезает ножницами из нее фрагмент, содержащий отрезок по абсциссе, два отрезка, перпендикулярных оси абсцисс и касающихся начала и конца кривой, и саму кривую. Затем взвешивает лист миллиметровой бумаги, площадь которого известна. Читатель может сам оценить точность такого интегрирования, если учесть, что масса вырезанного фрагмента близка к 5 г, а точность взвешивания на обычных аналитических весах составляет 0,0002 г.

Измерения и расчеты, проводимые по уравнению (6 ‑ 36), дают возможность находить только отношение летучестей. Абсолютное значение летучести отдельного газа при заданном давлении установить, пользуясь только этим уравнением, невозможно. Таким образом, одного уравнения для создания таблиц значений летучести, которые позволили бы накапливать экспериментальные данные для последующего применения, оказалось недостаточно. Потребовалось ввести дополнительные условия для представления летучести в виде справочной величины. Таким дополнительным условием было установление точки начала отсчета летучести.