Зависимость химического потенциала от состава идеальных газовых систем

Первыми идеальными системами, к которым мы обратимся, являются идеальные газовые смеси. Напомним, какими свойствами они обладают.

Смеси подчиняются уравнению состояния идеального газа

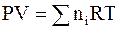, (6 - 21)

в котором n_i - число молей газа i, и закону Дальтона, согласно которому общее давление смеси равно сумме парциальных давлений газов

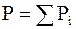. (6 - 22)

Для числа молей n_i каждого газа выполняется уравнение

. (6 - 23)

При постоянной температуре для системы с постоянным объемом выполняются равенства:

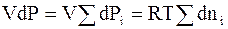. (6 - 24)

При постоянной температуре уравнение Гиббса - Дюгема (6 - 19) приобретает форму:

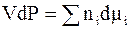. (6 - 25)

Из равенства левых частей уравнений (6 - 24) и (6 - 25) следует

.

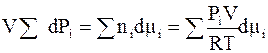или

. (6 - 26)

В идеальной смеси газы не влияют друг на друга (ведут себя независимо). В связи с этим разность в каждой скобке должна быть равна нулю:

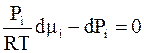. (6 - 27)

Напомним, что уравнение (6 - 27) выполняется при постоянной температуре. Его интегрирование дает

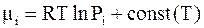. (6 - 28)

В уравнении (6 - 28) для каждой температуры получается своя постоянная интегрирования. Для краткости записи ее чаще всего обозначают m_i^o. С учетом этого традиционная форма зависимости химического потенциала от парциального давления идеального газа приобретает следующий вид:

(6 - 29)

При постоянном общем давлении и при постоянной температуре выполняется равенство

.

Отношение числа молей данного вещества n_i к общему числу молей Sn_i является молярной долей веществаx_i.

Введем обозначение

,

с помощью которого выразим зависимость химического потенциала газа от его молярной доли в идеальной газовой смеси

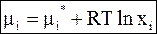. (6 - 30)