Химический потенциал. Химическим потенциаломmi называется парциальная молярная энергия Гиббса при постоянном давлении, постоянной температуре и постоянных числах молей остальных
Химическим потенциаломmi называется парциальная молярная энергия Гиббса при постоянном давлении, постоянной температуре и постоянных числах молей остальных веществ
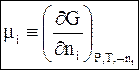 (6 - 6)
(6 - 6)
С учетом равенства (6 - 6) уравнение (6 - 4) принимает следующий вид:
dG = VdP - SdT + Smidni. (6 - 7)
Так как энергия Гельмгольца может быть выражена
F = G - PV,
то ее приращение выразится так:
dF = dG - PdV - VdP,
dF = -PdV - SdT + Smidni. (6 - 8)
Для других функций
H = G + TS;
U = G - PV + TS
найдем
dH = VdP + TdS + Smidni, (6 - 9)
dU = -PdV + TdS + Smidni. (6 - 10)
Следовательно, химический потенциал можно выразить как парциальную молярную величину любой характеристической термодинамической функции:
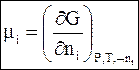 (6 - 11)
(6 - 11)
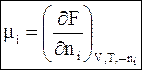
 (6 - 12)
(6 - 12)
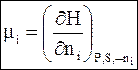 (6 - 13)
(6 - 13)
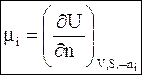 (6 - 14)
(6 - 14)
Введенный Дж. У. Гиббсом химический потенциал оказался очень удобной для термодинамических расчетов величиной.
Рассмотрим одно из важнейших свойств химического потенциала.
Пусть находящаяся в равновесии система состоит из F фаз, которым присвоим номера 1,2. ...f (фазой называются части системы, имеющие одинаковый состав и свойства в каждой точке). Во всех фазах содержится вещество i.
Данное условие поясним следующими примерами.
В равновесии с паром находится водный раствор этанола. В этом случае в равновесии находятся две фазы, одна из которых жидкая (раствор), а другая газообразная (пар). Этанол находится в обеих фазах.
Система состоит из двух слоев жидкости: верхний слой - бензол, а нижний слой - вода. В систему вводится кристаллический йод, который растворим как в воде, так и в бензоле. Через определенное время в системе устанавливается равновесие и обе жидкости содержат растворившийся в них йод.
В приведенных выше примерах этанол и йод являются теми веществами, которые находятся во всех фазах системы.
В равновесных системах все фазы имеют одинаковую температуру. Система находится также при постоянном давлении. Поэтому условием равновесия является минимум энергии Гиббса, т.е.
dG = 0.
Перенеся из фазы 1 в фазу 2 бесконечно малое число молей dni вещества i, изменим энергию Гиббса первой фазы на следующую величину:
dG(1) = mi(1)(-dni).
Знак минус означает, что вещество i выводится из фазы 1. Верхний индекс у символа химического потенциала и энергии Гиббса показывает, что они относятся к первой фазе.
Изменение энергии Гиббса второй фазы составит
dG(2) = mi(2)dni.
Так как энергия Гиббса обладает свойством аддитивности, то общее изменение энергии Гиббса в системе находим суммированием изменений в отдельных фазах
dG = dG(1) + dG(2) = mi(1)(-dni) + mi(2)dni = 0.
Следовательно,
mi(1) = mi(2).
Далее, перенося то же бесконечно малое число молей dni вещества i из фазы 2 в фазу 3 и т.д., получим остальную часть системы равенств:
mi(2) = mi(3), ..., mi(f-1) =mi(f).
Окончательно условие фазового равновесия можно записать в следующей форме
mi(1) =mi(2) =...=mi(f) . (6 - 15)
Уравнение (6 - 15) означает, что химический потенциал одного и того же вещества во всех равновесных фазах равен одной и той же величине.
Применение химического потенциала существенно упрощает рассмотрение химического равновесия.
Когда автор начинал преподавательскую деятельность, он слышал одну любопытную историю, в которой подчеркивалось значение работ Гиббса по введению химического потенциала. Много лет спустя в пересказе по памяти она выглядит следующим образом.
Джозайя Уиллард Гиббс, один из основоположников современной формы термодинамики, пришедшей на смену термодинамики циклов Томсона, Клаузиуса, Максвелла, родился в 1839 г. В первой половине ХХ в. термодинамика была наиболее популярной дисциплиной у физиков и химиков и столетие со дня рождения Гиббса в Москве отмечалось с большой торжественностью. Юбилейное заседание проводилось в самой крупной научной аудитории того времени - в Большой аудитории Политехнического музея. Основным докладчиком был переводчик на русский язык и комментатор работ Гиббса Владимир Ксенофонтович Семенченко. Слушателей поразили две вещи из его доклада. Говоря с восторгом о Гиббсе, В. К. Семенченко, чтобы еще больше подчеркнуть ту тщательность, с которой Гиббс подходил к отделке своих работ, с большим пафосом сказал: «Гиббс отличался необычайной научной добросовестностью, совершенно невиданной в наши дни». Акцентируя внимание на этих словах, он наклонился к президиуму, в котором сидели видные ученые и другие деятели. Получился весьма назидательный поклон. Продолжая свое выступление, он подошел к одному из крупнейших достижений Гиббса - введению в термодинамику химического потенциала. Эта часть доклада была выражена следующим образом. Последовала фраза: «Введя в термодинамику химический потенциал, Гиббс создал совершенную науку, можно сказать, науку для дураков!». Несомненно, читатель понял смысл этой фразы правильно, а именно: химический потенциал сделал термодинамику стройной и логичной наукой, в которой вопросы равновесия решаются приравниванием химических потенциалов.
Автор увидел В.К.Семенченко через несколько десятилетий после описываемых событий и был поражен эмоциональностью и образностью выступления уже достаточно немолодого человека. Поражало его стремление сделать свое выступление доступным каждому слушателю. Он все время апеллировал к слушателям, сопровождая свою речь жестами. Ему хотелось, чтобы каждый проникся основной идеей его выступления. Можно представить, какова же была его энергия и с каким темпераментом он делал доклад на том заседании!
Автор полагает, что эта анекдотическая история не исказит образ В.К.Семенченко, замечательного человека и ученого, создавшего теорию критических фазовых переходов, к которым относятся переходы металлов из ферромагнитного в парамагнитное состояние и др.
Дата добавления: 2015-07-24; просмотров: 1201;
