Примеры использования характеристических функций. Уравнения Гиббса - Гельмгольца

Покажем возможности использования метода характеристических функций на примере вывода уравнения Клапейрона - Клаузиуса.

Ранее это уравнение было получено по методу циклов. Здесь мы используем свойства энергии Гиббса.

При равновесии двух сосуществующих фаз (жидкость ‑ пар, твердое вещество - жидкость, твердое вещество - пар) обе фазы находятся в тепловом равновесии (имеют общую температуру Т) и механическом равновесии (находятся при одинаковом давлении Р). При постоянных Р и Т условием равновесия является минимум энергии Гиббса. Следовательно,

G = G_min; dG = 0.

Это означает, что насколько увеличится энергия Гиббса одной фазы, настолько уменьшится энергия Гиббса другой фазы:

dG = dG₁ - dG₂.

Переход из одной фазы в другую не сопровождается полезной работой, а только механической работой. Поэтому система, состоящая из двух фаз чистого вещества, является простой системой, и приращение энергии Гиббса каждой фазы определяется уравнением (5 - 25)

dG₁ = V₁dP - S₁dT, dG₂ = V₂dP - S₂dT.

Отсюда

(V₁dP -S₁dT) - (V₂dP - S₂dT) = 0

или

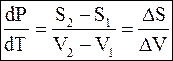. (5 - 62)

Уравнение (5 - 62) является новой формой уравнения Клапейрона -Клаузиуса.

Принимая во внимание уравнение (4 - 14), в соответствии с которым изменение энтропии при фазовом переходе определяется изменением энтальпии DH_p.t., вновь возвращаемся к привычной форме уравнения Клапейрона - Клаузиуса:

.

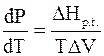Используя энергию Гиббса и энергию Гельмгольца, можно сравнительно легко найти температурную зависимость полезной работы и полной работы системы.

Действительно, при постоянном давлении и постоянной температуре конечное приращение энергии Гиббса можно выразить следующим образом:

DG = D(H - TS) = DH - TDS (5 - 63)

Из выражения (5 - 32), устанавливающего равенство энтропии и производной энергии Гиббса по температуре со знаком минус, вытекает

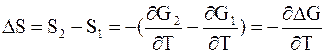. (5 - 64)

Подстановка (5 - 64) в (5 - 63) дает

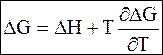. (5 - 65)

При постоянной температуре приращение энергии Гельмгольца в соответствии с равенством (5 - 12) равно

DF = DU - TDS. (5 - 66)

Используя равенства (5 - 30) и (5 - 66), получим

. (5 - 67)

Так как приращение энергии Гиббса при постоянных Р и Т равно полезной работе со знаком минус согласно равенству (5 - 45), а приращение энергии Гельмгольца - полной работе со знаком минус согласно равенству (5 - 47), то зависимость полезной работы и полной работы от температуры выражается следующим образом:

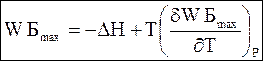(5 - 68)

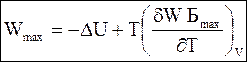(5 - 69)

Уравнения (5 - 68) и (5 - 69) называют уравнениями Гиббса - Гельмгольца.

Очень часто в название уравнения Гиббса - Гельмгольца включают и генетически связанные с ними уравнения (5 ‑ 65) и (5 - 67). Более того, можно встретить использование этого названия для абсолютных значений функций

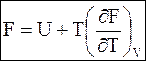(5 - 70)

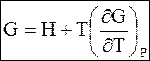(5 - 71)

Уравнения (5 - 65), (5 - 67), (5 - 68) и (5 - 69) представляют собой дифференциальную форму уравнений Гиббса - Гельмгольца.

Интегрирование уравнения (5 - 65) проводят, используя очевидное равенство

. (5 - 72)

Разделив обе части равенства (5 - 65) на Т², с учетом выражения (5 - 72) получим

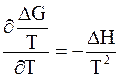. (5 - 73)

Форма (5 - 73) удобна для интегрирования. Разделив переменные, получим:

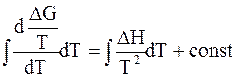. (5 - 74)

В случае интегрирования от нулевой температуры уравнение (5 - 74) принимает следующий вид:

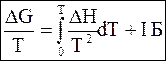. (5 - 75)

В уравнение (5 - 75) входит постоянная интегрирования I`.

Если в системе протекает химическая реакция, то температурная зависимость ее теплоты выражается уравнением Кирхгофа (2 - 10). Подставив в уравнение (2 - 10) в качестве нижнего предела интегрирования нулевую абсолютную температуру, получим

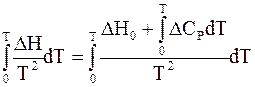. (5 - 76)

Подстановка правой части уравнения (5 - 76) в уравнение (5 - 75) приводит к полной интегральной форме уравнения Гиббса - Гельмгольца, из которой следует, что приращение энергии Гиббса, а также максимальную полезную работу и условие равновесия системы можно было бы определить только по термохимическим данным, т.е. по результатам калориметрических измерений изменения энтальпии и теплоемкости. Для этого достаточно было бы установить величину константы интегрирования I`.

Однако ни из первого, ни из второго начала термодинамики установить величину константы интегрирования невозможно. Более детально с проблемой нахождения константы интегрирования, которую иногда называют термодинамически неопределимой константой, и решением этой проблемы мы познакомимся в дальнейшем.

С помощью уравнений (5 - 65) и (5 - 75) могут решаться различные задачи.

Уравнение (5 - 75), как уже отмечалось, принципиально может быть использовано для расчета приращения энергии Гиббса по калориметрическим данным, а уравнение (5 - 65) - для приращения энтальпии по температурной зависимости максимальной полезной работы. Для этого используют уравнение (5 - 68) в следующей форме:

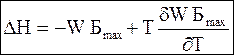(5 - 77)

Интересно сравнить условия калориметрического определения приращения в ходе химической реакции и приращения энтальпии, определяемого по температурной зависимости максимальной полезной работы химической реакции.

Калориметрическое определение DН означает, что реакция проводится без совершения полезной работы, т.е. в абсолютно необратимом процессе, а DН, оцениваемое по температурной зависимости полезной работы, предполагает проведение квазистатического процесса.