Стандартное термодинамическое состояние для газов

Стандартное термодинамическое состояние было введено как общее начало отсчета летучести для всех газов.

Так как свойства всех газов различны, то в реальных условиях у них не может быть общих точек на кривой f=f(P). Следовательно, общее для всех газов состояние может быть только воображаемым.

Наиболее удобно предполагать, что все свойства у различных газов совпадут, если они превратятся (воображаемо!) в идеальные газы.

Исторически сложилось так, что в течение многих десятилетий в качестве единицы давления использовалась атмосфера (атм.), причем 1 атм равна 1,01325×10⁵ Па. Нетрудно понять, что в стандартном состоянии газ должен находиться именно при этом давлении.

Хотя в последующие годы система единиц изменилась, давление идеального газа в стандартном состоянии осталось прежним, т.е. равным 1 атм.

Определение стандартного термодинамического состояния для газов таково:

Стандартное термодинамическое состояние газа при данной температуре представляет собой воображаемое состояние в виде идеального газа при давлении 1,01325×10⁵ Па.

Рассмотрим процесс перехода газа из стандартного состояния в заданное состояние, которому соответствует летучесть f.

Будем придерживаться следующего обязательного условия:

Все величины, относящиеся к стандартному состоянию или отсчитываемые от него, обозначаются символом ^о, который ставится вверху справа от определяемой величины.

По этой причине в стандартном состоянии давление и равная ему летучесть будут обозначаться следующим образом: f^o = P^o =1.01325×10⁵ Па.

Первая стадия перехода из стандартного состояния в заданное состояние газа включает расширение газа. Поскольку в стандартном состоянии он наделен свойствами идеального газа, то расширение его (не следует забывать, что речь идет об изотермической функции) должно происходить по изотерме идеального газа до очень маленького давления P* или летучести f*. Изменение энергии Гиббса на этой стадии равно

.

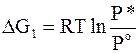При очень малых давлениях свойства реального газа фактически совпадают со свойствами идеального газа. Поэтому различие между изотермами идеального газа и изотермами реального газа в этих условиях отсутствуют. В связи с этим переход с изотермы идеального газа на изотерму реального газа не вызовет никаких изменений в системе. Следовательно, для второго этапа процесса изменение энергии Гиббса окажется равным нулю.

Третий этап представляет собой сжатие по изотерме реального газа от летучести f* до летучести в заданном состоянии f. Изменение энергии Гиббса на этом этапе равно

.

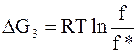Общее изменение энергии Гиббса в результате всех этапов равно

.

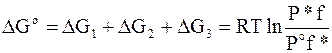Так как P^o =f^o и f*»P*, то окончательно имеем

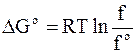(6 - 37)

или

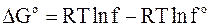. (6 - 38)