Химические потенциалы веществ в реальных системах

Для того, чтобы найти зависимость химического потенциала вещества в газовой фазе от его летучести, проведем следующий воображаемый процесс.

Из системы, в которой газ i находится в стандартном состоянии и его химический потенциал равен m_i^o , перенесем его бесконечно малое число молей dn_i в реальную систему, в которой летучесть газа равна f_i, а химический потенциал равен m_i.

Этот процесс сопровождается изменением энергии Гиббса

,

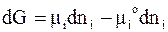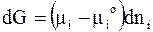.(6 - 39)

С другой стороны, изменение летучести от f^o до f_i приводит к изменению энергии Гиббса для 1 моль

,

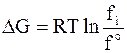а для dn_i молей изменение энергии Гиббса составляет

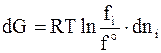. (6 - 40)

Приравнивая правые части равенств (6 - 39) и (6 - 40), получим

.

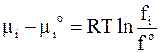Включая стандартную летучесть в общую константу, окончательно имеем

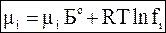(6 - 41)

Уравнение (6 - 41) отражает зависимость химического потенциала от летучести в реальных газовых смесях.

Обратимся к реальным растворам в конденсированных системах.

Пусть имеются две системы: конденсированная система в виде вещества i в стандартном состоянии и реальный раствор, содержащий это вещество.

Совершим следующий воображаемый процесс.

Перенесем бесконечно малое число молей dn_i вещества i из первой системы во вторую и найдем изменение энергии Гиббса на всех стадиях этого процесса.

Квазистатический переход из чистой жидкости (или твердого вещества) в пар не приводит к изменению энергии Гиббса. Переход dn_i моль из пара над чистым веществом с летучестью f_i^o в пар над раствором с летучестью f_i приводит к изменению энергии Гиббса

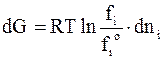. (6 - 42)

Последующий квазистатический переход из пара в жидкость не приводит к изменению энергии Гиббса. Таким образом, изменение энергии Гиббса для всего процесса определяется уравнением (6 - 42).

Если химический потенциал вещества i в стандартном состоянии равен m_i^o, а химический потенциал в растворе равен m_i, то изменение энергии Гиббса при переносе dn_i молей вещества из одной системы в другую можно представить следующим образом:

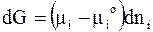. (6 - 43)

Из равенства правых частей уравнений (6 - 42) и (6 ‑ 43) следует

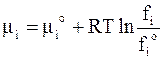. (6 - 44)

Уравнение (6 - 44), показывающее зависимость химического потенциала от состава конденсированной системы, имеет принципиальное отличие от подобного уравнения для газовых систем.

В газовых системах стандартная летучесть одинакова для всех газов, а для конденсированных систем стандартная летучесть является специфической величиной каждого вещества. Ее не включают в общую константу.

Отношение летучести вещества над его раствором к летучести в стандартном состоянии называется термодинамической активностьюa_i вещества в растворе

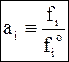(6 - 45)

В идеальных растворах термодинамическая активность совпадает с молярной долей вещества и выражение (6 - 45) можно рассматривать как обобщение закона Рауля для реальных систем.

Нетрудно заметить, что

в стандартном состоянии термодинамическая активность вещества равна 1.

Введение термодинамической активности упрощает запись основного выражения для химического потенциала, придавая ему форму:

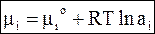(6 - 46)