Сродство химической реакции

Вновь запишем уравнение реакции в общей форме

n₁A₁ +n₂A₂ + ... +n_iA_i +...= n₁`B<sub>1</sub> +n<sub>2</sub>`B₂ +...+n_j`B_j +... (7 - 1)

Пусть в ходе реакции количество вещества A₁ изменяется на dn_a1 моль, вещества А₂ - на dn_a2, ..., вещества A_i - на dn_ai, ..., вещества В₁ - на dn_b1, ...

В соответствии с одним из важнейших стехиометрических законов химии - законом эквивалентов - числа молей связаны между собой соотношением

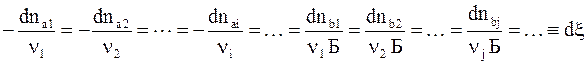(7 - 2)

Вводимая соотношением (7 - 2) величина x получила несколько названий: химическая переменная, число пробегов химической реакциии др.

Используя химическую переменную, введем еще одну величину А, которая называется сродством химической реакции.

Приводимое ниже выражение является определением сродства

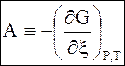(7 - 3)

Так как при постоянных Р и Т изменение энергии Гиббса со знаком минус равно максимальной полезной работе (-dG = dW`_max), а бесконечно малое изменение химической переменной dx не изменяет состава системы, то

сродство имеет смысл максимальной полезной работы реакции при условии, что количества вступивших в реакцию и образовавшихся в ходе ее веществ равны стехиометрическим коэффициентам в уравнении этой реакции, а состав системы остается практически неизменным.

Подстановка -dW`_max вместо dG в выражение (7 - 3) приводит к еще одной форме определения сродства

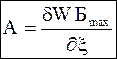. (7 - 3а)

Напомним, что в общем случае приращение энергии Гиббса определяется равенством

.

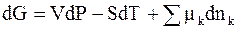Согласно определению сродства частная производная энергии Гиббса берется при постоянном давлении и постоянной температуре. Для данного случая можно записать

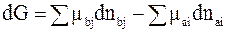. (7 - 4)

Учитывая, что

,

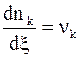из равенств (7 - 3) и (7 - 4) следует

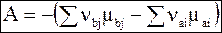(7 - 5)

Уравнение (7 - 5) играет огромную роль при описании химических процессов и химического равновесия.

Отметим, что сродство может быть выражено и с помощью других термодинамических функций, приращения которых при постоянных соответствующих параметрах равны максимальной полезной работе со знаком минус.

В дополнение к уравнениям (7 - 3) и (7 -3а) запишем следующие уравнения:

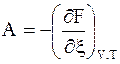; (7 - 3b)

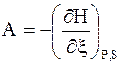; (7 - 3c)

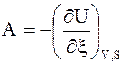. (7 - 3d)