Частные производные функции нескольких переменных
Определение 6. Частной производной по х от функции z = f(х, у) называется предел отношения частного приращения Dхz по х к приращению Dх при стремлении Dх к нулю.
Частная производная по х от функции z = f(х, у) обозначается одним из символов
 ,
, 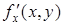 ,
, 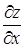 ,
, 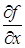 .
.
Таким образом, по определению,
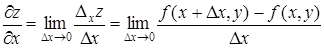 .
.
Аналогично частная производная по у от функции z = f(х, у) определяется как предел отношения частного приращения Dуz по у к приращению Dу при стремлении Dу к нулю. Частная производная по у обозначается одним из символов
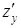 ,
, 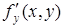 ,
, 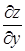 ,
, 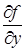 .
.
Таким образом,
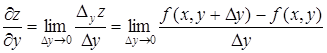 .
.
Заметив, что Dхz вычисляется при неизменном у, а Dуz при неизменном х, мы можем определения частных производных сформулировать так: частной производной по х от функции z = f(х, у) называется производная по х, вычисленная в предположении, что у – постоянная. Частной производной по у от функции z = f(х, у) называется производная по у, вычисленная в предположении, что х – постоянная.
Из этого определения ясно, что правила вычисления частных производных совпадают с правилами, указанными для функций одной переменной, и только требуется каждый раз помнить, по какой переменной ищется производная.
Пример 14. Дана функция 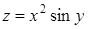 ; требуется найти частные производные
; требуется найти частные производные 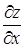 и
и 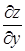 .
.
Решение. 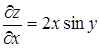 ,
, 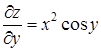 .
.
Пример 15. z = xy.
Здесь 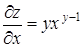 ,
, 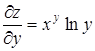 .
.
Частные производные функции любого числа переменных определяются аналогично. Так, если имеем функцию и четырех переменных х, у, z, t:
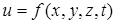 ,
,
то
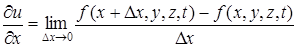 ,
,
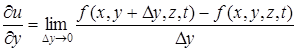 и т.д.
и т.д.
Пример 16. 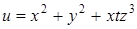 .
.
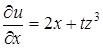 ,
, 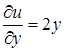 ,
, 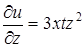 ,
, 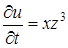 .
.
Дата добавления: 2015-07-24; просмотров: 948;
