Приложение дифференциала к оценке погрешности при вычислениях

Пусть некоторая величина и является функцией величин х, у, z, …, t:

и = f(x, y, z, …, t),

причем, определяя каким-то способом значения величин х, у, z, …, t, мы допускаем погрешности Dх, Dу, …, Dt. Тогда значение и, вычисленное по неточным значениям аргументов, получится с погрешностью

Dи = f(x + Dх, y + Dу, z + Dz, …, t + Dt) - f(x, y, z, …, t).

Ниже мы займемся оценкой погрешности Dи, если известны погрешности Dх, Dу, …, Dt.

При достаточно малых абсолютных значениях величин Dх, Dу, …, Dt можем приближенно заменить полное приращение полным дифференциалом:

.

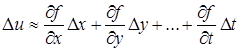Здесь значения частных производных и значения погрешностей аргументов могут быть как положительными, так и отрицательными. Заменяя их абсолютными величинами, получим неравенство

.

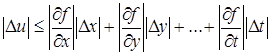Если через |D^*x|, |D^*y|, …, |D^*t|, |D^*u| обозначим максимальные абсолютные погрешности соответствующих величин (границы для абсолютных величин значений погрешностей), то можно, очевидно, принять

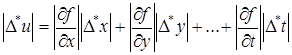. (19)

Отношение погрешности Dх некоторой величины к приближенному значению х этой величины называется относительной погрешностью величины. Будем его обозначать dх:

.

Максимальной относительной погрешностью величины х называется отношение максимальной абсолютной погрешности к абсолютной величине х и обозначается ½d^*х½:

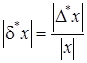. (20)

Для оценки максимальной относительной погрешности функции и разделим все числа равенства (19) на ½и½=½f(x, y, z, …, t½:

,

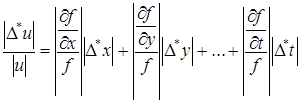но

, , …, .

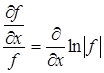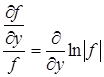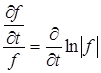Поэтому равенство (20) можно переписать так:

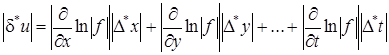, (21)

или коротко

.

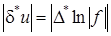Из формул как (20), так и (21) следует, что максимальная относительная погрешность функции равняется максимальной абсолютной погрешности логарифма этой функции.

Замечание. Если и = х – у, то 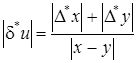. Если х и у близки, то может оказаться, что 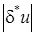будет очень велика по сравнению с определяемой величиной х – у. Это обстоятельство следует учитывать при производстве вычислений.

Задания для самостоятельной работы

Найти полный дифференциал и полное приращение функции u(x,y) в точке (2; 1) при Dх = 0.1, Dу = 0.1.

41. u = x+y .	42. .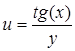
43. 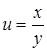.	44. .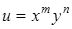

Найти полный дифференциал функции трех переменных х, у, z.

45. 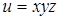.	46. .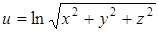
47. 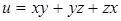.	48. .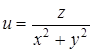

Заменяя приращение функции дифференциалом, приближенно вычислить:

49. 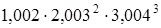.	50. .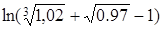
51. 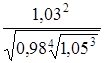.	52. .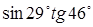

53.На сколько изменятся диагональ и площадь прямоугольника со сторонами

x = 6 м и y = 8 м, если первая сторона увеличится на 2 мм, а вторая сторона уменьшится на 5 мм?

54. При измерении радиуса основания R и высоты H цилиндра были получены следующие результаты:R=2,5±0,1 мм;Н=4,0±0,2 мм. Скакой абсолютной погрешностью D и относительной погрешностью d может быть вычислен объем цилиндра?

55. Стороны треугольника a =200 м ± 2 м, b =300 м ± 5 м и угол между ними

С = 60^о±1^о. С какой абсолютной погрешностью может быть вычислена третья сторона?

7. Производная сложной функции. Полная производная.

Полный дифференциал сложной функции