Применение полного дифференциала в приближенных вычислениях

Пусть функция z = f(х, у) дифференцируема в точке (х, у). Найдем полное приращение этой функции

,

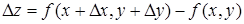откуда

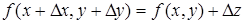. (15)

Подставляя в формулу (15) вместо Dz, согласно (13), развернутое выражение для dz (14), получим приближенную формулу

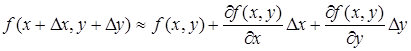(16)

верную с точностью до бесконечно малых высшего порядка относительно Dх и Dу.

Покажем, как используются формулы (13) и (16) для приближенных вычислений.

Пример 19. Вычислить объем материала, нужного для изготовления цилиндрического стакана следующих размеров (рис. 14): радиус внутреннего цилиндра R, высота внутреннего цилиндра Н, толщина стенок и дна стакана k.

		Рис. 4

Решение. Дадим два решения этой задачи: точное и приближенное.

Точное решение. Искомый объем v равен разности объемов внешнего цилиндра и внутреннего цилиндра. Так как радиус внешнего цилиндра равен R + k, а высота H + k, то

или 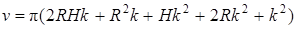. (17)

Приближенное решение. Обозначим через f объем внутреннего цилиндра, тогда 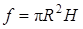. Это – функция двух переменных R и Н. Если увеличим R и Н на k, то функция f получит приращение Df; но это и будет искомый объем v, т.е. v = Df.

На основании соотношения (15) имеем приближенное равенство v » df, или 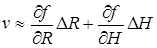. Но так как 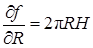, , 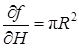DR = DН = k, то получаем

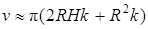. (18)

Сравнивая результаты (17) и (18), видим, что они отличаются на величину 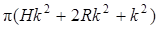, состоящую из членов второго и третьего порядка малости относительно k.

Применим эти формулы к числовым примерам.

Пусть R = 4 см, Н = 20 см, k = 0.1 см.

Применяя (17), получим точно

.

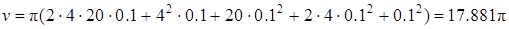Применяя формулу (18), получим приближенно

.

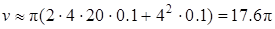Следовательно, приближенная формула (18) дает ответ с погрешностью, меньшей 0.3p, что составляет 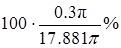, т.е. менее 2% измеренной величины.