Глава 4. Приложение производных к исследованию функций.

Использование производных позволяет прояснить многие особенности в поведении функций. Наиболее важными особенностями функций являются интервалы монотонности и точки экстремумов функций.

Если функция относится к классу дифференцируемых монотонных функций, то ее производная сохраняет знак на интервале монотонности, причем возрастающая функция имеет положительную производную, а убывающая – отрицательную. Действительно, если Δх > 0, то так как

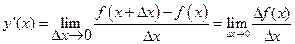
то знак производной совпадает со знаком приращения функции.

Для возрастающих функций

Δf(x) > 0 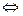f `(x) > 0,

для убывающих функций

Δf(x) < 0 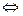f `(x) < 0.

Функция имеет локальный максимум (минимум) в точке х₀, если она определена как в точке х₀, так и в окрестности этой точки и значение функции в точке х₀ больше (меньше), чем ее значения во всех соседних точках: т. е.

f(х₀) > f(x) в точках максимума

f(х₀) < f(x) в точках минимума

для всех х из окрестности точки х₀.

Минимумы и максимумы функции объединены единым понятием – экстремумы. До точки максимума функция возрастает, следовательно, ее производная положительна

f `(x) > 0

после точки максимума – убывает, производная отрицательна

f `(x) < 0.

Для точки минимума первоначально функция убывает

f `(x) < 0,

а потом возрастает

f `(x)>0).

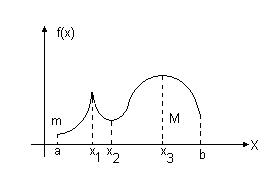
В самих точках экстремумов производная или равна нулю (обычный экстремум) или не существует (острый экстремум). На рис. 4.1 функция имеет экстремумы в точках х₁, х₂ и х₃, причем в точке х₁ – острый максимум, а в точках х₂ и х₃ обычный минимум и максимум.

Тем самым, в точках экстремумов функции производная равна нулю или не существует (необходимое условие экстремума) и меняет знак с «+» на «-» в точках максимумов и с «-» на «+» в точках минимумов (достаточные условия экстремума).

Точки, в которых производная равна нулю называются стационарными точками. Не все стационарные точки являются точками экстремумов. В стационарных точках надо проверять достаточное условие экстремума.

Замечание. Не надо путать наибольшее и наименьшее значение и экстремумы. Экстремум достигается всегда внутри промежутка, а наибольшее и наименьшее значения могут достигаться и в точках экстремумов и на границах промежутка и в точках разрыва. На рис. 4.1 точка х₃ является точкой максимума и в ней также достигается наибольшее значение, наименьшее значение достигается в точке а, т.е. на границе промежутка.

Функция называется выпуклой (выпуклость вверх) на интервале (a,b), если график функции лежит под любой касательной в каждой точке интервала, на всем интервале выпуклости вторая производная отрицательна f ``(x) < 0.

Функция называется вогнутой (выпуклость вниз) на интервале (a,b), если график функции лежит над любой касательной в каждой точке интервала, на всем интервале вогнутости вторая производная положительна f ``(x) > 0 (рис.4.2).

Следовательно, в точках экстремумов вторая производная имеет определенный знак (достаточное условие экстремума по второй производной):

в точках максимумов f ``(x₀) < 0 ,

в точках минимумов f ``(x₀) > 0.

Точки, в которых вторая производная равна нулю и меняет знак (с «+» на «-» или с «-» на «+» ) называются точками перегиба (рис. 4.2).

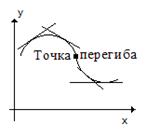
Например:

y = x² e^-x 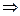y`= 2x e^-x - x² e^-x = x e^-x ( 2 – x);

y`= 0 если x = 0 или x = 2, это стационарные точки.

y``= (2 x e^-x – x²e^-x))’ = 2e^-x - 2 x e^-x – 2 x e^-x + x² e^-x = e^-x(2 - 4x + x²);

y``= 0 если x_1,2 =2 ,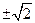

это точки перегиба

y``(0) = 2 > 0,

следовательно в точке х = 0 минимум,

y``(2) = -2e^-2 < 0, следовательно в точке х = 2 максимум.

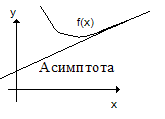
Прямая y = kx + b называется асимптотической прямой (наклонной асимптотой) для функции f(x), если при х→∞ расстояние от переменной точки графика функции М до прямой стремится к нулю (рис. 4.3). При этом

, .

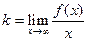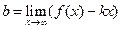Пример 1. y = x e^-x.

, .

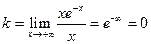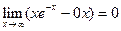Прямая у = 0 является наклонной (горизонтальной) асимптотой.

Пример 2. Исследовать и построить график функции .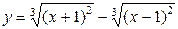

Решение.

1. Заданная функция определена и непрерывна на всей числовой оси

.

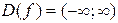2. Функция нечетная, ибо 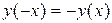, ее график будет симметричен относительно начала координат. Поэтому достаточно построить график для

.

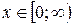3. График функции пересекается с осями координат только в начале координат, так как .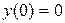

4. Исследуем функцию на наличие асимптот:

а) вертикальных асимптот график функции не имеет;

б) наклонная асимптота имеет уравнение .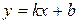

,

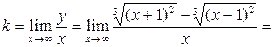
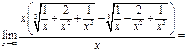
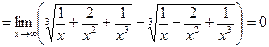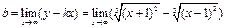
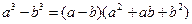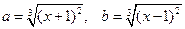Используем формулу , где . Домножим числитель и знаменатель на

.

.

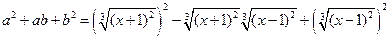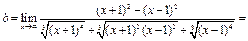
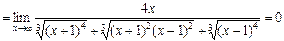Таким образом, уравнение асимптоты .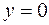

5. Исследуем функцию на экстремум

.

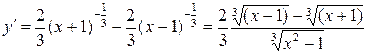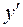нигде не обращается в нуль; 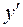не существует в точках 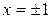, которые являются критическими.

Исследуем знак производной на интервале [0; ∞)

0 1

Рис. 4.4.

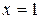есть точка максимума, .

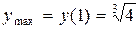6. Исследуем график функции на выпуклость и вогнутость

.

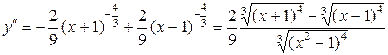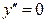в точке 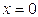; 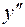не существует в точках 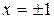. Эти точки могут быть абциссами точек перегиба.

Исследуем знак второй производной на интервале [0; ∞)

0 1

Рис. 4.5.

не является точкой перегиба.

Основываясь на полученных результатах исследования, строим график функции на интервале [0; ∞), затем симметрично полученному графику относительно начала координат на интервале (- ∞; 0)

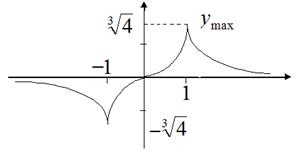
Рис. 4.6.

Пример 3. Найти наибольшее и наименьшее значения функции

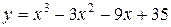на отрезке [-4; 4].

1. Найдем критические точки функции 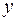, лежащие внутри отрезка [-4; 4], и вычислим ее значения в этих точках:

;

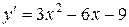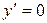в точках 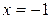и .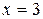

Эти точки лежат внутри отрезка [-4; 4] и являются критическими. Других критических точек нет, так как производная существует всюду. Значение функции в критических точках: 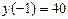и .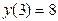

2. Вычислим значения функции на концах отрезка [-4; 4]: 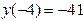и .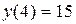

3. Сравнивая все вычисленные значения функции во внутренних критических точках и на концах отрезка, заключаем: наибольшее значение функции 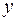на отрезке [-4; 4] равно 40 и достигается ею во внутренней критической точке 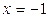, а ее наименьшее значение равно -41 и достигается на левой границе отрезка .

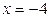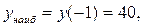
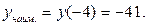
Во многих геометрических, физических и технических задачах требуется найти наибольшее или наименьшее значение величины, связанной функциональной зависимостью с другой величиной.

Для решения такой задачи следует, исходя из ее условия, выбрать независимую переменную, а затем найти искомое наибольшее или наименьшее значение полученной функции. При этом интервал изменения независимой переменной, который может быть конечным или бесконечным, также определяется из условия задачи.

Пример 4. Из трех одинаковых тонких досок изготовить желоб с наибольшим поперечным сечением.

Решение. Поперечное сечение желоба будет представлять равнобочную трапецию (рис. 4.7), площадь которой S зависит от наклона боковых сторон. Выберем за независимую переменную угол α между боковой стороной и высотой трапеции и выразим через эту переменную исследуемую площадь S.

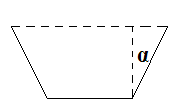
Рис. 4.7.

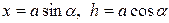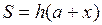и или ,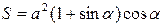

где, по смыслу задачи, α может изменяться на отрезке .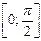

Далее найдем наибольшее значение функции 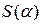на отрезке .

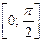Найдем критические точки функции 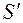, лежащие внутри этого отрезка

.

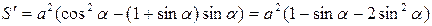Приравнивая производную 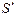к нулю, получим уравнение

,

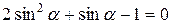решая которое, как квадратное, найдем 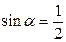и .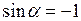

Из всех точек α, определяемых этими двумя уравнениями, внутри отрезка 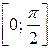лежит только одна точка 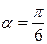. Эта точка является критической, в ней выполняются все необходимые для этого условия. Производная 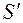существует всюду, поэтому других критических точек нет.

Вычислим значение функции S в найденной внутренней критической точке и на концах отрезка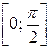

.

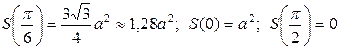Сравнивая эти значения, заключаем: наибольшее значение функции S на отрезке 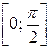достигается во внутренней точке .

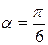Таким образом, желоб из трех одинаковых досок будет иметь наибольшее поперечное сечение, когда это сечение представляет разнобочную трапецию, верхнее основание которой вдвое больше нижнего.

Пример 5. Найти размеры цилиндрической закрытой цистерны с заданным объемом V и с наименьшей полной поверхностью.

Решение. Обозначив радиус и высоту цилиндра через r и h, а его полную поверхность через 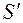, получим

.

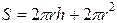Здесь переменные r и h не являются независимыми, а связаны между собой равенством 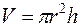, так как согласно условию, цилиндр должен иметь заданный объем V. Определяя из этого равенства h и подставляя в выражение полной поверхности, найдем

,

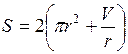где r изменяется в интервале .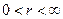

Выразив таким образом исследуемую полную поверхность цилиндра S через одну переменную r, найдем теперь ее наименьшее значение при изменении r в интервале (0; ∞).

Найдем критические точки

.

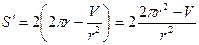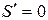в единственной точке 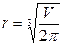, которая лежит в рассматриваемом интервале. Эта точка является критической, других критических точек нет.

Исследуем найденную критическую точку по знаку второй производной в этой точке

,

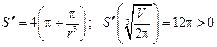откуда следует, что критическая точка 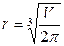есть точка минимума.

Функция 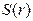непрерывна в интервале (0; ∞). Поэтому согласно свойству непрерывных функций единственный минимум функции S в интервале (0; ∞) совпадает с ее наименьшим значением в этом интервале.

При 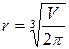получим

.

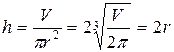Следовательно, цилиндрическая закрытая цистерна, имеющая любой заданный объем, будет иметь наименьшую полную поверхность, когда ее осевое сечение представляет квадрат.