Частное и полное приращение функции
Рассмотрим линию пересечения поверхности
z = f(x, y)
с плоскостью y = const, параллельной плоскостью Oxz.
Так как в этой плоскости у сохраняет постоянное значение, то z вдоль кривой, у которой у постоянное, будет меняться только в зависимости от изменения х. Дадим независимой переменной х приращение Dх; тогда z получит приращение, которое называется частным приращением z по х и обозначается через Dхz, так что
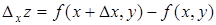 .
.
Аналогично, если х сохраняет постоянное значение, а у получает приращение Dу, то z получает приращение, называемое частным приращением z по у. Это приращение обозначают символом Dуz:
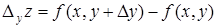 .
.
Приращение Dуz функция получает «вдоль линии» пересечения поверхности z = f(х, у) с плоскостью x = const, параллельной плоскости Oyz.
Наконец, сообщив аргументу х приращение Dх, а аргументу у – приращение Dу, получим для z новое приращение Dz, которое называется полным приращением функции z и определяется формулой
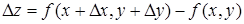 .
.
Надо заметить, что, вообще говоря, полное приращение не равно сумме частных приращений, т.е. 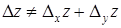 .
.
Пример 11. z = xy.
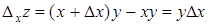 ;
; 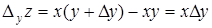 ;
;
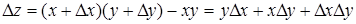 .
.
При х = 1, у = 2, Dх = 0,2, Dу = 0,3 имеем 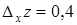 ,
, 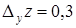 ,
, 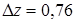 .
.
Аналогичным образом определяются частные и полное приращения функции любого числа переменных. Так, для функции трех переменных u = = f(x, y, t) имеем
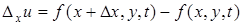 ,
,
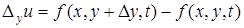 ,
,
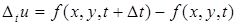 ,
,
 .
.
Дата добавления: 2015-07-24; просмотров: 1456;
