Геометрическое изображение функции двух переменных

Рассмотрим функцию

z = f(x, y), (1)

определенную в области G на плоскости Оху (эта область может быть, в частности, и всей плоскостью), и систему прямоугольных декартовых координат Охуz (рис. 1). В каждой точке (х, у) восставим перпендикуляр к плоскости Оху и на нем отложим отрезок, равный f(х, у).

Тогда мы получим в пространстве точку Р с координатами

x, y, z = f(х, у).

Геометрическое место точек Р, координаты которых удовлетворяют уравнению (1), называется графиком функции двух переменных. Из курса аналитической геометрии мы знаем, что уравнение (1) в пространстве определяет некоторую поверхность. Таким образом, графиком функции двух переменных является поверхность, проектирующаяся на плоскость Оху в область определения функции. Каждый перпендикуляр к плоскости Оху пересекает поверхность z = f(x, y) не более чем в одной точке.

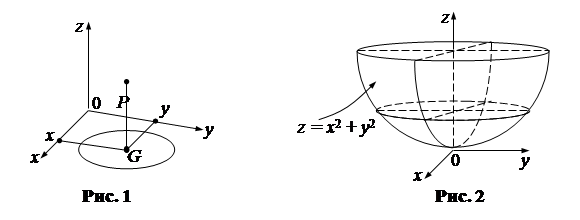Пример 10. Графиком функции z = х² + у², как известно из аналитической геометрии, является параболоид вращения (рис. 2).

Замечание. Функцию трех и более переменных изобразить с помощью графика в пространстве невозможно.