Уравнение Аррениуса

С. Аррениус предложил полутеоретический метод оценки влияния температуры на константу скорости химической реакции, который впоследствии получил дополнительное обоснование.

Идея метода Аррениуса заключается в следующем.

Предположим, что протекает обратимая реакция:

k₁

A D B.

k ₋₁

Константа равновесия этой реакции равна:

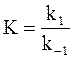. (11 - 3)

Зависимость константы равновесия от температуры определяется уравнением изобары Вант-Гоффа:

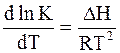. (11 - 4)

Гипотеза Аррениуса утверждает, что тепловой эффект реакции DH можно представить в виде разности двух величин:

DH = E₁ – E ₋₁, (11 - 5)

причем E₁ относится к прямой реакции, а E₋₁ - к обратной.

С учетом равенств (11 - 3) и (11 - 5) уравнение (11 - 4) можно записать в следующей форме:

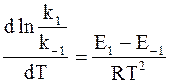
или

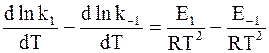. (11 - 6)

Так как прямая и обратная реакции принимаются независимыми друг от друга, то уравнение (11 - 6) можно рассматривать как разность двух независимых уравнений. Первое из них содержит k₁ и E₁, а второе - k₋₁ и E₋₁:

;

.

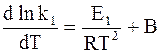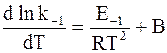Аррениус предположил в согласии с экспериментальными данными, что постоянная В, появляющаяся при разделении уравнения (11 - 6) на составляющие части, равна 0. С учетом этого для любой частной реакции можно записать обобщенную форму уравнения:

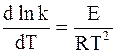. (11 - 7)

Уравнение (11 - 7) называется дифференциальной формой уравнения Аррениуса. Входящая в него величина Е, имеющая размерность Дж/моль, называется энергией активации.

Интегрирование уравнения (11 - 7) дает:

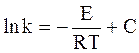, (11 - 8)

где С - постоянная интегрирования.

Обозначив e^C = k₀, окончательно имеем:

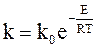. (11 - 9)

Уравнение (11 - 9) называется уравнением Аррениуса.

При выводе уравнения Аррениуса, кроме использования нескольких произвольных допущений, предполагалось, что тепловой эффект реакции не зависит от температуры. Такое предположение возможно для сравнительно узкого температурного интервала. В связи с этим интервал температур, в котором можно определять энергию активации, также должен иметь ограничения.

Для графического определения энергии активации по экспериментальным данным используют в качестве координат обратную температуру и логарифм константы скорости (рис. 11 ‑ 1). Тангенс угла наклона прямой в этих координатах равен отношению энергии активации к универсальной газовой постоянной.

Следует отметить, что подобный характер зависимости от температуры имеют и другие кинетические величины: коэффициент диффузии, текучесть (величина, обратная вязкости). Энергию активации диффузии и вязкого течения также находят по углу наклона прямой в координатах: обратная температура, логарифм кинетической величины. Эти координаты называются координатами Аррениуса.

Представляет интерес зависимость между температурным коэффициентом реакции g и энергией активации Е. Для этого воспользуемся уравнениями (11 - 1) и (11 ‑ 9).

Подстановка констант k_T и k_T+10, которым соответствует температура Т и Т+10, в уравнение (11 - 9) с учетом уравнения (11 - 1) дает:

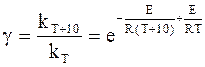
или, принимая, что T>>10, получим,

, (11 - 10)

а также

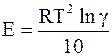. (11 - 11)

Эмпирическое правило Вант-Гоффа показывает, что для реакций, протекающих при температуре, близкой к комнатной (Т » 300 К), энергия активации находится в пределах 20¸40 кДж/моль.