Обратимая реакция
Рассмотрим систему реакций:
k1
A D B. (a)
k−1
Частная реакция
A ® B (b)
называется прямой реакцией, а частная реакция
A B (с)
называется обратной реакцией.
Скорость исчезновения вещества А по реакции (b) описывается уравнением:
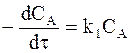 , (10 - 10)
, (10 - 10)
а его накопление по реакции (с) - уравнением:
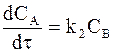 . (10 - 11)
. (10 - 11)
Изменение концентрации вещества А по обеим реакциям в соответствии с принципом независимого протекания реакций составит:
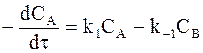 . (10 - 12)
. (10 - 12)
Для решения уравнения (10 - 12) введем следующие граничные условия: к началу реакции (t = 0) концентрации веществ А и В соответственно равны a и b. Если к моменту времени t концентрация вещества А изменится на –х, то концентрация вещества В в соответствии с условием материального баланса изменится на х. Следовательно,
CA = a – x,
CB = b – x,
и уравнение (10 - 12) принимает следующий вид:
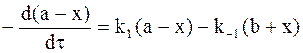 . (10 - 13)
. (10 - 13)
После преобразования уравнения (10 - 13) получим:
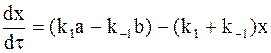
и
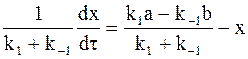 . (10 - 14)
. (10 - 14)
Обозначив
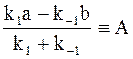 ,
,
с учетом граничных условий (х = 0 при t = 0) интегрированием уравнения (13 - 14) получим:
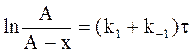 . (10 - 15)
. (10 - 15)
Из уравнения (10 - 15) следует, что предельное значение х, соответствующее t = ¥, равно константе А, то есть
А = х¥.
При очень длительном протекании обратимой реакции в системе наступает равновесие. Равновесные концентрации СА,¥ и СВ,¥ зависят от исходных концентраций веществ и констант скоростей:
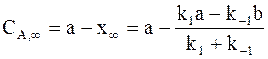 ;
;
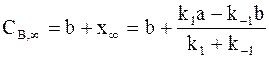 ;
;
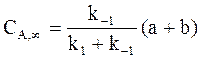 ; (10 - 16)
; (10 - 16)
 . (10 - 17)
. (10 - 17)
 Рис. 10 - 2. Кинетические кривые для исходного вещества и продукта.
Рис. 10 - 2. Кинетические кривые для исходного вещества и продукта.
|
Отметим, что отношение равновесных концентраций продуктов к концентрациям исходных веществ представляет собой константу равновесияK. Из равенств (10 - 16) и (11 - 17) следует: 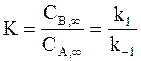 . (10 - 18)
. (10 - 18)
Выражение (10 - 18) показывает, что полученные результаты полностью согласуются с представлениями о динамическом характере химического равновесия.
Типичный ход кинетических кривых для исходных веществ и продуктов обратимой реакции первого порядка показан на рис. 10 - 2.
Последовательные реакции
Последовательными реакцияминазывают реакции, протекающие в несколько стадий. Вещества, образующиеся на каждой стадии и принимающие участие в дальнейшем превращении, называются промежуточными соединениями.
Рассмотрим простейшую схему последовательных реакций:
k1 k2
A ¾® B ¾® C.
В данной схеме А является исходным веществом, В - промежуточное соединение, С - продукт реакции.
Кинетика расходования исходного вещества описывается обычным уравнением необратимой реакции первого порядка:
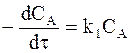 . (а)
. (а)
Кинетика накопления вещества В описывается тем же уравнением (а), которое перепишем в иной форме:
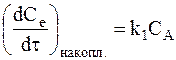 . (b)
. (b)
Кинетика расходования вещества В на образование продукта реакции описывается также уравнением необратимой реакции первого порядка:
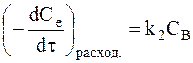 . (с)
. (с)
Общая скорость изменения концентрации промежуточного продукта в соответствии с принципом независимого протекания реакций определяется как алгебраическая разность скоростей реакций (b) и (с):
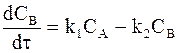 . (10 - 19)
. (10 - 19)
В уравнениях (a), (b) и (с) в качестве переменных используются концентрации веществ А и В. Кроме того, переменной является концентрация продукта реакции. Для удобства записи обозначим концентрации веществ А, В и С соответственно X, Y и Z. Если до начала реакции в системе содержится только вещество А, концентрация которого равна а, то концентрации всех веществ должны быть связаны между собой в соответствии с условием материального баланса:
X + Y + Z = a.
Для еще большего упрощения записи последующих уравнений используем нормированные концентрации:
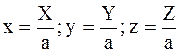 , то есть СА = ах, СВ = ay, CC = az.
, то есть СА = ах, СВ = ay, CC = az.
Нормированная концентрация вещества А изменяется по времени в соответствии с уравнением (9 - 14), которое в данной форме записи принимает вид:
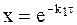 . (10 - 20)
. (10 - 20)
Дифференциальное уравнение (10 - 19), описывающее изменение по времени концентрации промежуточного соединения, можно записать так:
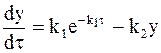 . (10 - 21)
. (10 - 21)
Уравнение (10 - 21) является неоднородным дифференциальным уравнением первой степени. Первым этапом его решения является решение соответствующего однородного уравнения. В данном случае таким однородным уравнением является:
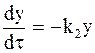 . (10 - 22)
. (10 - 22)
Его решение таково:
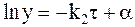 . (10 - 23)
. (10 - 23)
Возникающая при интегрировании уравнения (10 - 22) величина a не является константой, а представляет собой функцию времени t, так как это уравнение послужит заменой неоднородного уравнения.
Уравнению (10 - 23) можно придать иную форму:
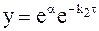
или, обозначив 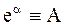 , получим
, получим
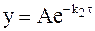 . (10 - 24)
. (10 - 24)
Величина А, входящая в уравнение (10 - 24), также зависит от времени t. В связи с этим дифференцирование уравнения (10 ‑ 24) дает:
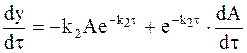 . (10 - 25)
. (10 - 25)
Вычитая из уравнения (10 - 25) уравнение (10 - 21) и учитывая, что левый член правой части уравнения (10 - 25) равен −k2y, получим:

или
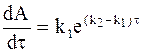 . (10 - 26)
. (10 - 26)
После интегрирования уравнения (10 - 26) находим зависящую от времени величину А:
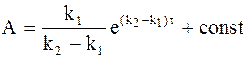 . (10 - 27)
. (10 - 27)
Ее подстановка в уравнение (10 - 24) приводит к новому уравнению, выражающему зависимость концентрации промежуточного соединения от времени:
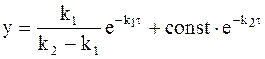 . (10 - 28)
. (10 - 28)
Для того, чтобы найти постоянную интегрирования, входящую в уравнение (10 - 28), воспользуемся исходными условиями: в начальный момент промежуточное соединение отсутствует (t = 0, y = 0), т.е.
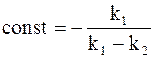 .
.
Окончательный вид уравнения для концентрации промежуточного соединения таков:
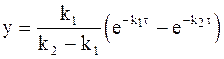 . (10 - 29)
. (10 - 29)
Концентрацию продукта реакции можно сравнительно легко установить из условия:
z = 1 - (x + y).
Следовательно,
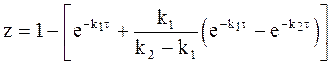
или
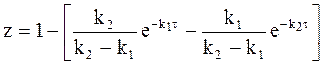 . (10 - 30)
. (10 - 30)
Уравнения (10 - 20), (10 - 24) и (10 - 30) позволяют описать кинетические кривые всех трех веществ А, В и С. Однако прежде, чем анализировать ход кинетических кривых, убедимся в правильности полученного результата. С этой целью для проверки воспользуемся уравнением (10 - 30), для которого возьмем два крайних случая:
скорость первой реакции А¾®В во много раз меньше скорости второй реакции В¾®С;
скорость второй реакции В¾®С во много раз меньше скорости первой реакции А¾®В.
Первому случаю отвечает соотношение констант скоростей k1 << k2, а второму - k2 << k1.
В первом случае выполняются приближения:
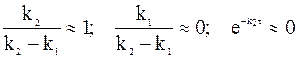 ,
,
а во втором случае - приближения:
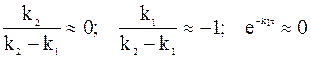 .
.
С учетом этих приближений уравнение (10 - 30) трансформируется в два однотипных уравнения:
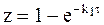 при k1<< k2,
при k1<< k2,
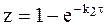 при k2<< k1.
при k2<< k1.
Таким образом, получены варианты уравнения (10 - 15), определяющего кинетику необратимой реакции первого порядка по накоплению продукта реакции.
Данный результат находится в полном согласии с постулатом о том, что кинетика реакции в целом определяется самой медленной стадией и показывает правильность полученных уравнений.
Окончательную форму уравнений, описывающих ход кинетических кривых для каждого вещества, получим, перейдя от нормированных концентраций к обычным, то есть с учетом, что СA =ax, CB = ay, CC = az:
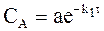 , (10 - 31)
, (10 - 31)
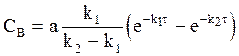 , (10 - 32)
, (10 - 32)
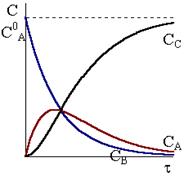 Рис. 10 - 3. Кинетические кривые для реакций
Рис. 10 - 3. Кинетические кривые для реакций 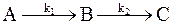 в случае k1»k2. в случае k1»k2.
|
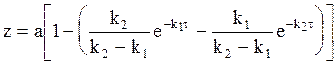 . (10 - 33)
. (10 - 33)
Кинетические кривые для последовательных реакций с различным соотношением констант скоростей показаны на рис. 10 ‑ 3, 10 ‑ 4 и 10 - 5.
Максимум на кинетической кривой CB = CB(t) наступает при условии 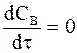 и в соответствии с уравнением (10 - 21) в точке максимума выполняется соотношение:
и в соответствии с уравнением (10 - 21) в точке максимума выполняется соотношение:
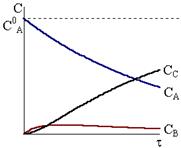 Рис. 10 - 5. Кинетические кривые для реакций
Рис. 10 - 5. Кинетические кривые для реакций 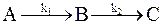 в случае k1<<k2. в случае k1<<k2.
|
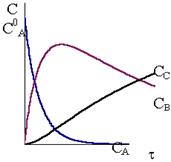 Рис. 10 - 4. Кинетические кривые для реакций
Рис. 10 - 4. Кинетические кривые для реакций 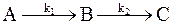 в случае k1>>k2 в случае k1>>k2
|
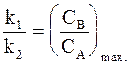 . (10 - 34)
. (10 - 34)
Положение максимума на кинетической кривой найдем дифференцированием уравнения (10 - 32):
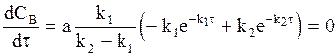 .
.
После преобразований получим:
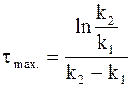 . (10 -35)
. (10 -35)
Из формулы (10 - 35) следует, что положение максимума промежуточного соединения не зависит от концентрации исходного вещества, а определяется лишь соотношением между константами скорости.
Соотношение между константами скорости также влияет на форму кинетической кривой промежуточного соединения. При большом отношении k1/k2 концентрация промежуточного соединения очень быстро возрастает, а затем после максимума начинает медленно уменьшаться. Для больших отношений k2/k1 характерен медленный подъем концентрации промежуточного соединения и более размытый максимум.
Если константа реакции превращения промежуточного соединения меньше константы превращения исходного вещества, то всегда можно дождаться такого времени реакции, чтобы выполнялось условие:
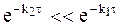
или
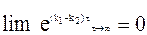 .
.
Поэтому разделив уравнение (10 - 32) на уравнение (10 - 31), получим:
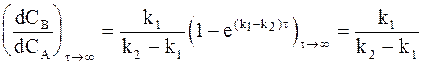 . (10 - 36)
. (10 - 36)
Наступающее через достаточно длительное время соотношение между концентрациями называется переходным отношением(или переходным равновесием).
Если выполняется более жесткое условие k2>>k1, то соотношение между концентрациями принимает вид:
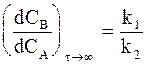 (10 - 37)
(10 - 37)
или
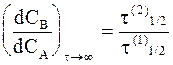 , (10 - 38)
, (10 - 38)
где t(1)1/2 и t(2)1/2 - соответственно время полупревращения исходного вещества и промежуточного соединения.
Формулы (10 - 37) и (10 - 38) отражают вековое соотношениемежду концентрациями (или вековое равновесие). Они представляют значительный интерес для выяснения времени полураспада радиоактивных элементов по содержанию в образцах руды элементов, составляющих радиоактивное семейство. Кроме того, аналитическое определение концентраций промежуточных веществ дает возможность оценивать константы скорости отдельных этапов многостадийных реакций.
Дата добавления: 2015-07-22; просмотров: 858;
