Теория активных столкновений

Теория активных столкновений (она также называется теорией активных соударений) явилась первой теорией, количественно объяснившей данные кинетических исследований на основе молекулярно-кинетических представлений. Эта теория разработана как для случая бимолекулярных столкновений, так и для тримолекулярных столкновений. Ниже рассматриваются основные результаты, полученные для бимолекулярных столкновений.

В основе теории использованы следующие предположения (постулаты теории активных соударений):

1) Первым актом возможного взаимодействия молекул является их столкновение.

2) Столкновение молекул может служить причиной превращения молекул только в том случае, если энергия столкновения превышает или по крайней мере равна некоторой критической величине e_а. Столкновения с энергией, равной этой величине или превышающей ее, называются активными.

3) Активные столкновения приводят к благоприятному исходу, то есть к началу химической реакции, если расположение молекул в момент столкновения соответствует данной реакции.

Первый постулат теории означает, что теория не рассматривает реакции, протекающие под непрерывным воздействием квантов света или частиц высокой энергии (гамма-квантов, электронов и т.д.).

Второй постулат теории предполагает, что для начала химического превращения сталкивающиеся молекулы должны обладать энергией, достаточной для преодоления вполне определенного энергетического барьера. Если энергия столкновения молекул оказывается меньше e_а, то происходит упругий удар без каких-либо химических превращений.

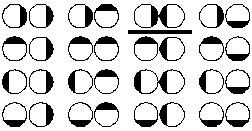Рис. 12 - 1. Условное представление положений молекул в момент столкновения.

Из третьего постулата следует, что не все активные столкновения эффективны. На рис. 12 - 1 условно показаны возможные положения двух молекул в момент столкновения. Условные благоприятные для реакции положения на рисунке подчеркнуты. Отношение числа положений, благоприятствующих химической реакции, к общему числу возможных положений молекул в момент столкновения называется стерическим фактором. Расчеты показывают, что обычно величина стерического фактора близка к 10⁻².

Молекулярно-кинетическая теория дает возможность рассчитывать число столкновений с определенной энергией.

Общее число столкновений Z₀ в единичном объеме газовой фазы определяется уравнением:

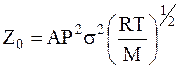, (12 - 1)

в котором A - числовой коэффициент, P - давление, s - эффективный диа­метр столк­нове­ния, M - эффективная молярная масса сталкивающихся моле­кул.

Объединив все характеристики сталкивающихся молекул с числовым коэффициентом в единую константу для данной реакции b, уравнение (12 - 1) можно записать в следующей форме:

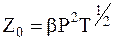. (12 - 2)

Число столкновений с энергией e_i подчиняется распределению Больцмана:

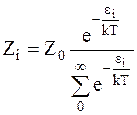. (12 - 3)

Число активных столкновений в единичном объеме представляет собой сумму всех столкновений, энергия которых не меньше e_а: _______________________

или

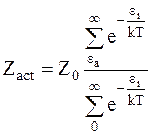. (12 - 4)

Число первичных химических превращений за единицу времени в единичном объеме в соответствии с третьим постулатом теории окажется равным:

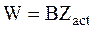, (12 - 5)

а с учетом уравнений (12 - 2) и (12 - 4):

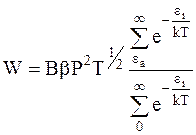. (12 - 6)

Для бимолекулярной реакции в газовой фазе зависимость скорости от давления выражается уравнением:

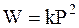. (12 - 7)

Сравнивая уравнения (12 - 6) и (12 - 7), получим уравнение для константы скорости реакции:

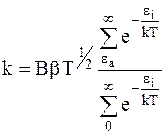. (12 - 8)

Прологарифмируем уравнение (12 - 8):

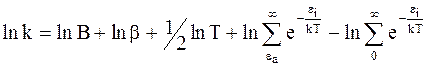
и продифференцируем по температуре:

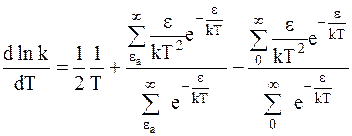. (12 - 9)

Пренебрегая в первом приближении величиной 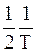и проведя преобразования, получим:

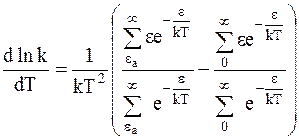. (12 - 10)

Для выяснения смысла отношений сумм, заключенных в скобках в правой части уравнения (12 - 10), отметим, что энергия всех активных соударений X_act равна:

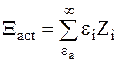. (12 - 11)

С учетом уравнения (12 - 3) равенство (12 - 11) приобретает следующий вид:

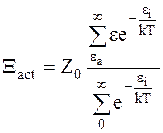. (12 - 12)

Отношение полной энергии активных столкновений к числу всех активных столкновений представляет собой среднюю энергию активного столкновения:

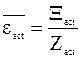. (12 - 13)

Сравнение уравнений (12 - 4), (12 - 12) и (12 - 13) показывает, что первое отношение сумм в уравнении (12 - 10) представляет собой среднюю энергию активного соударения:

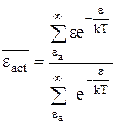. (12 - 14)

Второе отношение сумм представляет среднюю энергию всех столкновений в системе:

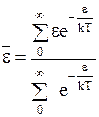. (12 - 15)

Равенства (12 - 14) и (12 - 15) позволяют представить уравнение (12 - 10) следующим образом:

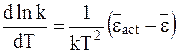. (12 - 16)

Умножение числителя и знаменателя правой части уравнения (12 - 16) на постоянную Авогадро дает:

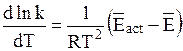, (12 - 17)

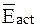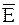где и - соответственно средняя энергия 1 моль активных соударений и средняя энергия 1 моль всех соударений.

Сравнение уравнения Аррениуса в дифференциальной форме (11 - 7) и уравнения (12 - 17) позволяет установить, чем же в соответствии с теорией активных соударений является энергия активации.

Энергия активации равна разности средней энергии 1 моль активных соударений и средней энергии 1 моль всех соударений:

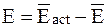. (12 - 18)

Напомним, что уравнение (12 - 18) имеет приближенный характер, так как при его выводе была исключена производная 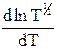. Уточненное значение энергии активации E_A со значением величины E выражается соотношением:

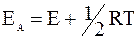. (12 - 19)

Иная трактовка энергии активации дается теорией активированного комплекса, которая будет рассмотрена в дальнейшем.